반응형
내 맘대로 Introduction

ICCV 2025에 가서 현장에서 본 포스터 중 눈에 띄어서 읽어본 논문. mesh의 surface point를 gaussian distribution으로 압축하고, 나중에 이 distribution만 갖고 다시 mesh surface points를 복원해낼 수 있도록 한 논문. 일종의 새로운 3D 표현법 이면서 압축률까지 가져갈 수 있는 방식. mesh resolution, 처리 가능한 point의 개수, watertightness 등 3D 데이터를 처리할 때 발목을 붙잡는 많은 이슈들이 있는데 그걸 해결해보고자 시도한 방식.
나 또한 메모리가 한정된 상황에서 그리고 데이터마다 퀄리티가 다른 상황에서 이걸 어떻게 동일한 기준으로 encoding하여 사용할 수 있을지 고민 중인데 좋은 insight를 주는 논문이라 생각한다.
다만 읽고 나니 flow matching을 통해 normal distribution과 surface point distribution을 맞추는 방식이라는 걸 알았다. 다시 말해 1개의 데이터를 인코딩하려면 diffusion model 하나급의 학습 리소스가 들어간다는 것.
학습이 완료되었다고 가정한다면 뭐 활용처가 있지만 실제로 이 데이터 1개를 압축하기 위해 A100 4장을 몇십 시간씩 쓴다는게 말이 안되는 듯 하다. 실효성은 그렇게 높지 않지만, 아이디어에 집중해서 봐야 좋을 듯.
데이터가 같은 그룹으로 잘 묶이기만 한다면 범용 모델도 만들 수 있지 않을까 싶다.
메모
 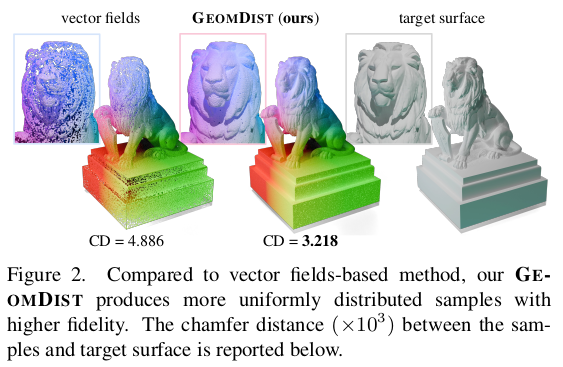 |
기존 방식들이 겪는 해상도를 맘대로 다룰 수 있는지 여부, 그리고 결과적으로 데이터 표현력이 얼마나 좋은지를 강조하며 시작. chamfer distance만으로 이정도를 학습한 것은 대단한 것 같다. |
  |
mesh로 표현된 3D 데이터가 있을 때 이를 하나의 distribution으로 표현할 수 있는가. mesh vertex,face의 개수와 상관없이 그 형상이 본질적으로 표현하는 모습을 담게 할 수 있는가. 형상을 하나의 distribution이라고 가정하고 normal distribution to 형상 distribution 간의 flow matching, 즉 diffusion process를 학습한다. 그렇다면 normal distr에서 무한히 샘플링한 다음 diffusion했을 때 무한 surface point를 얻을 수 있음. |
 |
 distribution to distribution 의 matching으로 접근하는 것. 그리고 네트워크 구조도 단순히 hash grid, MLP로 하면 안되고 적절한 구조가 있다는 것이 핵심. |
 |
|
  |
일단 컨셉을 확실하게 이해시키기 위해 학습은 됐다 치고 distribution to distribution 갖고 어떻게 surface point를 복원해낼 것인지를 설명한다. 그냥 diffusion model이 아니라 flow model로 학습시켰다는 가정이기 때문에 foward-inverse가 추적이 된다. 따라서 normal distribution에서 random sample point를 뽑고, 이를 매 t마다 조금씩 denoise하면서 이동량을 적분한다. 그러면 trajectory가 나오는데 이걸 끝까지 따라가면 최종 surface point에 도착함. 결과적으로 normal distribution에서 원하는 개수의 N sample point를 만들고 diffusion을 계속하면서 적분해주면 surface point N개를 얻을 수 있다. |
 |
forward sampling normal distribution to target distribution 방향으로 적분해나가는 것을 의미함. 실제로는 이것만 자주 쓸 것. |
  |
inverse sampling 이걸 실제로 쓰이진 않지만 flow model이기 때문에 구현이 가능함. 어떤 형상이 어떤 모양의 distribution으로 표현되는지 역추적하고 시각화할 때 도움이 됨.  |
  |
1. surface에서 매번 random sampling 2. noise를 조금 더해줌 3. denoiser가 noise를 맞추도록 수식(5)와 같이 학습 |
  |
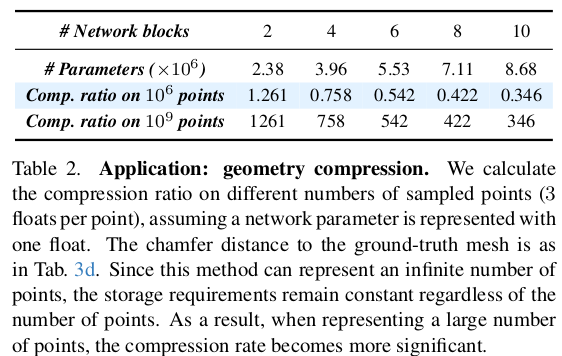 1 epoch에 2.5분 보통 1000epoch 돌리니까 샘플당 2500분이 걸린다 거의 40 시간.......................................................... 게다가 A100 4장 쓴다. |
 |
|
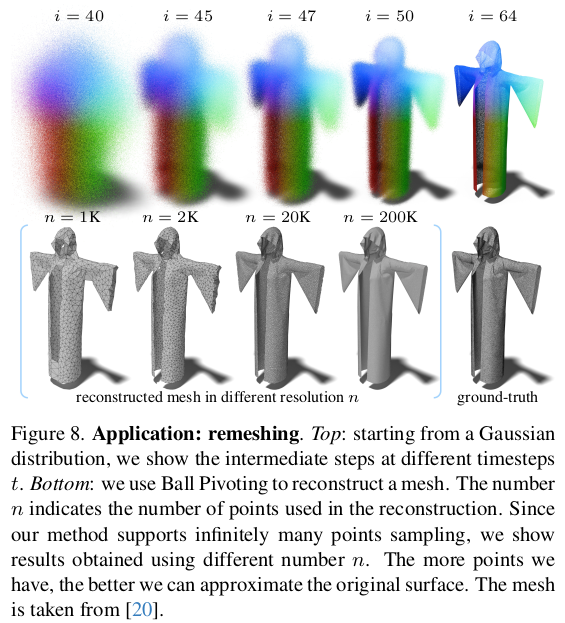
 학습만 잘 됐다 치면 의도한대로 무한 point 핸들링이 가능하다. 성능도 나름 괜찮고 |
 |
 xyz rgb를 같이 다루면서 학습시키면 색상도 당연히 커버 가능 (이러면 근데 학습 시간도 늘고 모델도 커지므로....) |
|
 이론상 다양한 primitives들도 같이 담는게 가능함. distribution은 uniform보다 normal로 사용하는게 잘 됨. |
 |
 학습 완료된 애를 inverse해서 normal distribution을 얻어보면 실제로 normal 같이 생기진 않음. distribution간 매칭이 완전 1대1 대응으로 이루어지진 않는다는 뜻. |
|
 |
smooth하게 diffusion 되어가는 모습 |
반응형