반응형
Lecture
Lecture 21: Eigenvalues and eigenvectors | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note

- eigenvalue와 eigenvector의 정의는 위와 같은 식에서 시작된다. Ax 라는 식을 function 처럼 x라는 벡터가 A라는 연산을 통해 Ax 라는 결과로 바뀌는 것이라고 생각해보자. f(x) = Ax 와 같은 것이다.
- 이 때 정말 특별한 x는 f(x)= Ax = λx 와 같이 Ax의 결과가 x 자신의 상수배인 형태를 보일 수 있다.
- 이 때 Ax와 x는 parallel 하다고 하며 이 때의 x를 eigenvector라고 하며 곱해지는 상수 λ를 eigenvalue라고 정의한다. (그 정의를 먼저 말하고 의미는 뒤에서 설명)
- 앞서 배운 내용과 연결고리를 만들기 위해서 λ가 0일 경우를 상상해보면, Ax=0x 이므로 eigenvector는 null space 상vector가 된다. 아직 뭔진 모르겠지만 eigenvector를 이전에 배운 개념을 포함하는 더 큰 정의라는 것을 받아들이면 되겠다.
- Ax=0x 예를 든 김에 하나 더 말해보면 A가 singular matrix일 경우, 즉 Ax=0 에서 x=0 말고 해를 갖는 경우에는 eigenvalue는 0이라고 할 수 있겠다.

- 추가 예시는 projection matrix다. Pb=p 와 같이 plane에 없는 vector b를 plane으로 proejction하여 plane 상 vector p를 얻게 도와주는 matrix인데
- Px가 x의 상수배일 경우를 상상해보면 2가지 경우만 존재한다. 첫번째는 x가 이미 projection plane 위에 있을 경우에 Px=λx가 가능하고 상수 λ는 1일 수 밖에 없다. 두번째는 x가 projection plane에 수직한 경우 가능하고 λ는 0이 된다.
- 따라서 projection matrix의 eigenvector는 projection plane 상의 아무 vector, eigenvalue는 1이거나 projection plane에 수직한 vector와 0이 된다.

- eigenvector와 eigenvalue를 직접 찾는 일은 꽤나 어렵다. 하지만 하나 단서로 사용할 중요한 사실은 matrix A의 대각 성분의 합이 모든 eigenvalue의 합과 같다는 사실이다. 즉 trace(A) == sum( all λ) 이다.
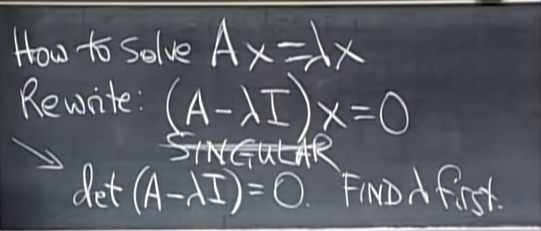
- eigenvector와 eigenvalue를 찾는 방법은 Ax=λx라는 식을 재정리하는 형태에서 발견할 수 있다.
- (A-λI)x=0는 형태로 정리했을 때 eigenvector 인 x가 0 외에 다양한 경우가 존재하려면 (A-λI)가 singular matrix여야 한다는 것을 이용한다. 즉, det(A-λI)=0을 만족해야 한다는 조건을 갖고 계산해낸다.
- 먼저 λ를 deterimant를 계산하는 과정에서 얻어낸 뒤, x는 nullspace 이므로 쉽게 찾을 수 있다.

- 예시는 위와 같다. 단순히 det(A-λI)=0 을 풀다 보면 λ에 관한 n차 방정식을 얻게 되고 이 해가 eigenvalue이다.
- 그리고 eigenvalue 를 하나씩 A-λI에 대입해보면서 null space를 찾으면 된다.
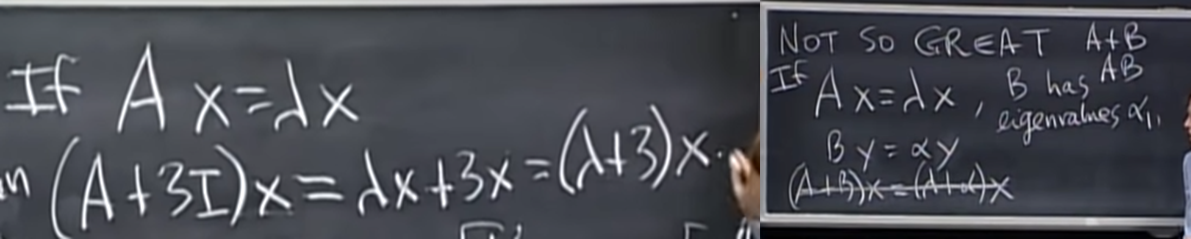
- 하나 독특한 특징은 A-λI를 이용해 풀다 보니 만약 A의 대각 성분에만 특정 값이 더해진 새로운 matrix A' 가 있다고 했을 때 A'의 eigenvalue는 A의 eigenvalue의 해당 특정값을 더한 것과 같다는 사실이다. 물론 대응되는 eigenvector도 동일하다. 위 왼쪽 사진 참고.
- 주의할 점은 대각 성분이 아닌 다른 위치 성분의 변화에는 곱과 합에 닫혀있지 않다는 사실이다. 우측 사진처럼 Ax+Bx =(A+B)x로 묶어서 풀 수 있을 것 같은데 실제로 A와 B는 eigenvector 가 다르기 때문에 Ax+By와 같다. 즉, 연산 못한다.

- 개념을 잘 이해하는데 도움이 되는 extreme 예시를 몇개 더 들어본다. 위 rotation matrix처럼 symmetric matrix에서 거리가 먼 anti-symmetric matrix일 경우에는 matrix 자체는 real matrix임에도 eigenvalue가 complex number로 존재할 수 있다. (symmetric matrix일 경우, real number로 존재함.)

- 중복된 eigenvalue를 갖는 matrix가 있다. 이 경우, independent eigenvector가 개수가 안 맞게 존재할 수도 있다.
- 이번 강의는 eigenvalue/eigenvector introduction에 가까워서 개념과 예시의 나열이었는데 다음 강의부터 그 의미를 분석할 것 같다.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 23. Differential equations exp(At) (0) | 2023.01.29 |
|---|---|
| [Linear algebra] 22. Diagonalization and powers of A (0) | 2023.01.28 |
| [Linear algebra] 20. Cramer's rule, inverse matrix, and volume (0) | 2023.01.27 |
| [Linear algebra] 19. Determinant formulas and cofactors (0) | 2023.01.25 |
| [Linear algebra] 18. Properties of determinants (0) | 2023.01.25 |