[Linear algebra] 23. Differential equations exp(At)

Lecture

https://ocw.mit.edu/courses/18-06-linear-algebra-spring-2010/resources/lecture-23-differential-equations-and-exp-at/

Lecture 23: Differential equations and exp(At) | Linear Algebra | Mathematics | MIT OpenCourseWare

 

Note

• 워낙 많이 쓰이는 행렬로 DE를 푸는 방법을 소개한다. 좌측 사진처럼 DE가 주어졌을 때 이를 푸는 방법은 A matrix를 정의하고 eigenvalue를 찾는 것으로 시작한다. 0과 -3을 찾았고 각각 대응되는 eigenvector도 찾았다. 
  
  

• 그 결과를 조합하기만 하면 solution을 구할 수 있다. DE 의 solution은 exp 함수를 이용해 표현한다는 사실을 미리 알고 있으니 위에서 구한 eigenvalue를 대입하여 식을 구성하면 solution이 된다. 
• c1, c2와 같은 계수는 initial condition u0를 알고 있을 경우 간단히 구할 수 있다. 결과적으로 DE 를 손쉽게 풀었다. 
  
  

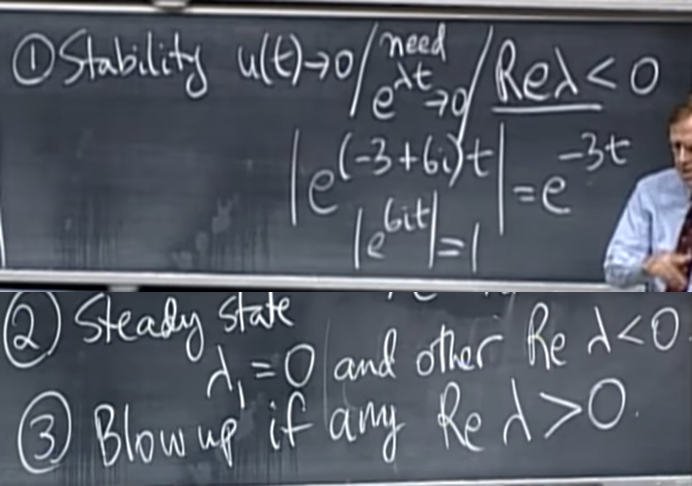
• 푸는 것 이외에 DE가 기술하고 있는 현상을 미리 분석하는 것이 가능한데, 가령 (1) 모든 eigenvalue가 음수일 경우 (복소수일 경우 실수부가 음수일 경우), u(t)->0 으로 수렴하므로 stable하다고 볼 수 있고, (2) eigenvalue 하나는 0 나머지는 음수일 경우, 특정값에 멈추는 steady state를 갖게 될 것이라고 볼 수 있으며, (3) 모든 eigenvalue가 양수일 경우, 시스템이 발산한다고 결론낼 수 있다. 
• 즉 eigenvalue를 이용해 DE를 푸는 것이 간편성 이상으로 시스템의 특징을 미리 알 수 있도록 도와준다. 
  
  

• 2x2 matrix일 경우, 눈에 잘 보이기 때문에 외워두는 것도 좋은데 trace(A) < 0 과 det(A) > 0을 만족하는지 보면 된다.
  
  

• 다시 DE로 돌아와서 solution을 구하는 것 외에 정리되는 형태를 다시 한 번 돌아보면 위와 같다. u=Sv (S: eigenvector matrix) 라고 정의해서 푸는 트릭을 사용하여 정리하면 위와 같이 깔끔하게 정리된다. 
• 따라서 위와 같이 정리할 수 있다는 것을 알면 더더욱 DE를 풀 때나 혹은 수학적 논리를 전개할 때 eigenvalue, eigenvector를 구하고 matrix 형태로 푸는 것이 효과적이라는 것을 알 수 있다.
  
  

• 게다가 matrix system이 아닌 일반 수 체계에서 통하는 taylor series expansion 같은 방식으로 구해도 같은 결과가 나올 정도로 matrix를 이용한 전개가 일반 수 체계와 거의 동일하게 동작하기 때문에 훌륭한 방식인 것이 맞다. 
  
  

• 더불어 n차 DE도 행렬을 이용하면 다수의 1차 DE로 분리할 수 있으므로 훨씬 용이한 장점도 있다.