반응형
Lecture
Lecture 18: Properties of determinants | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note
- determinant 는 행렬의 magic number로써 행렬 전체를 표현하는 대표 수 같은 개념이다.
- 일례로 determinant는 invertible test에 이용되며 그 외 활용도 다양하다.
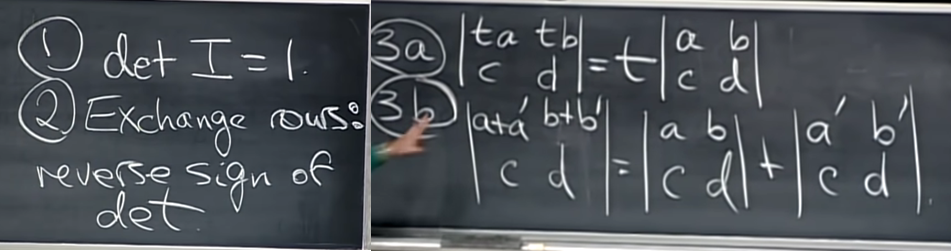
- 기억해야 할 특징 첫 번째는 identity matrix의 determinatn는 1이다. (당연해보이는데....)
- 두번째는 행렬에 row exchange 즉, permutation이 발생했을 시 determinant 값은 동일하고 부호가 바뀐다는 것이다. 이 때 부호 변화는 row exchange 횟수에 따라 다르다. 짝수일 경우 +변화, 홀수일 경우 -변화가 생긴다.
- 세번째는 제한적으로 linear하다는 것이다. 제한적이라는 것은 위 사진처럼 단 1개의 row에만 변화가 있고 다른 row에는 변화가 없을 때만 linearirty가 성립한다.

- 네번째는 같은 row가 중복되어 행렬 내에 존재할 경우, determinant는 0이다.
- 이는 두번째 특징을 이용해 간단히 증명할 수 있다. 같은 row i, j가 있다고 했을 때 i와 j row를 exchange한 결과는 본래 determinant 값의 minus 부호를 곱한 값이다. 이 때 같은 row 이므로 determinant는 같아야 하기도 하다. 부호가 다르면서 값이 같을 수 있는 것은 0 뿐이므로 중복 row가 있으면 determinant 는 무조건 0이다.
- 다섯번째는 elimination step을 거쳐도 determinant는 변하지 않는다는 것이다.
- 이또한 세번째 특징을 이용하면 간단히 증명할 수 있다. 우측 사진의 하단부를 참고하면 된다.
- 여섯번째 특징은 zero row가 하나라도 있으면 determinant 는 0이 된다.
- 이또한 세번째 특징을 이용하면 간단히 증명할 수 있다. zero row에만 scalar s를 곱했다고 했을 때 det(A)=s det(A)를 만족하는 수는 0뿐이다.
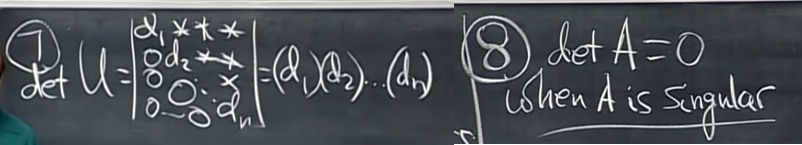
- 일곱번째 특징, upper triangular matrix의 determinant는 대각성분의 곱이다.
- 여덟번째 특징, matrix가 singular할 경우, determinant는 0이 나온다.
- 대우가 참이므로, determinant가 0이 아닐 경우, matrix가 non-singular하다는 증명이기 되기도 한다.

- 아홉번째 특징, 두 행렬의 곱에 대한 determinant는 각 행렬의 determinant의 곱이다. det(AB)=det(A) det(B)
- 이 특징을 이용하면 deter(A.inv) = 1/det(A)라는 것을 알 수도 있다. 증명은 위 사진 참고.
- det(2A) 와 같은 상수배가 헷갈릴 수 있는데 이는 단순히 2 det(A)가 아니다. 생각해보면 det(2I) det(A) 인데 2I는 diagonal matrix로 determinant각 2^n이 나온다. 따라서 2^n det(A)가 된다. volume처럼 생각해야 한다.

- 열번째 특징, transpose는 determinant는 바꾸지 않는다.
- 증명도 간단한데 위 사진에서 L 은 lower triangular matrix로 upper triangular matrix와 같이 대각 성분의 곱이 determinant이다. 그리고 L의 대각성분은 elimination의 결과로 전부 1인 상태이므로 det(L)=1이다. 이 사실을 대입해보면 알 수 있다.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 20. Cramer's rule, inverse matrix, and volume (0) | 2023.01.27 |
|---|---|
| [Linear algebra] 19. Determinant formulas and cofactors (0) | 2023.01.25 |
| [Linear algebra] 17. Orthogonal matrices and Gram-Schmidt (0) | 2023.01.21 |
| [Linear algebra] 16. Projection matrices and least squares (0) | 2023.01.21 |
| [Linear algebra] 15. Projection onto subspaces (0) | 2023.01.21 |