반응형
Lecture
Lecture 20: Cramer's rule, inverse matrix, and volume | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note

- matrix의 inverse는 위와 같이 determinant와 cofactor의 조합으로 표현할 수 있다.
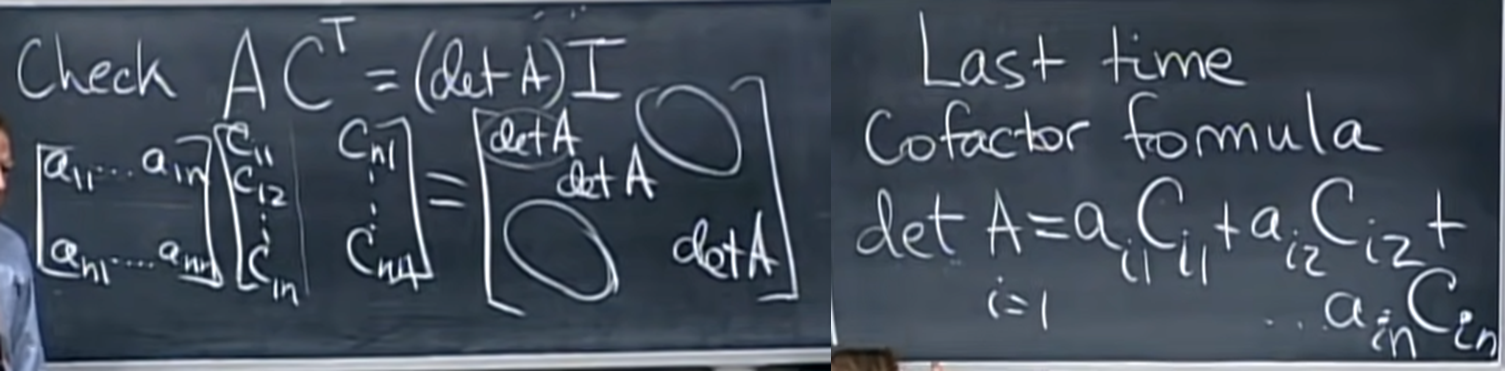
- 그냥 받아들이기 전에 확인을 조금 더 해보기 위해 위와 같이 AC.T = det(A) I 를 보면 대각 성분은 지난 시간에 배운 cofactor formula에 의해 det(A)임이 자명하게 들어난다.
- 대각 성분이 아닌 위치의 값들은 대응되지 않는 a와 c가 dot product 된 값들인데 이것도 자명하게 0이 된다. (사실 이 부분이 정확하게 이해되진 않는다..)

- 강의에서는 대충 2차원에서 설명해주는데, 위와 같이 대응되지 않는 a와 c가 곱해지는 경우를 보면 a(-b)+ba 처럼 필연적으로 0이 되는 구조를 띈다고 한다.
- 이는 아래 As matrix와 같이, 곱해지는 a's row, c's row가 중복된 값을 가질 때 벌어지는 상황과 같다고 한다.
- 중복된 row가 있을 경우 determinant가 0이 된다는 특징을 기억한다면 이 값이 0이 된다는 것을 알 수 있다.
- 대충 여기까지만 따라가고 받아들이면 될 것 같다.

- Cramer's rule은 Ax=b의 해를 det(A)와 cofactor를 이용해 표현한 식을 다시 한 번 변형된 형태로 정의할 수 있다는 말이다.
- 새로운 matrix B가 등장하는데, 이는 x_i 를 찾을 때, i 번째 column 만 b로 교체된 A matrix로 정의된다.
- 이 B matrix의 determinant를 찾으면 정확히 C.T b 의 dot product 형태와 같아짐을 알 수 있다. ( det(B)를 찾을 때 기준 value들을 b column으로 잡으면서 계산해야 한다. row 방향이 아니라)
- Cramer's rule은 수학적으로 의미는 있지만 공학적으로는 determinant 계산 횟수가 어마어마하게 늘어나기 때문에 연산 시간이 길어져 의미가 크게 없다. elimination으로 찾는 것이 낫다. 있다는 것만 알아두면 된다.

- determinant의 또 다른 수학적 의미를 알아보면, determinant는 어떤 box의 volume으로 해석할 수 있다.
- 여기서 어떤 box는 row vector (또는 column vector)가 생성하는 N차원 box를 의미한다.
- row vector든 column vector든 상관 없는 이유는, determinant를 계산할 때 기준 value와 cofactor를 계산하는 것을 row 방향으로 하든, column 방향으로 하든 똑같이 때문이다. det(A.T) = det(A).
- volume의 예를 들면, 3차원 matrix에서 3개의 vector가 만드는 찌그러진 cube가 있다.

- Orthogonal matrix일 경우에는 각 vector가 orthonormal vector이기 때문에 N차원 cube를 만든다. 다만 이리저리 회전된 cube가 되겠다.
- 개념 상 volume이 음수가 될 순 없지만, vector의 순서에 따라 음수가 생길 순 있다. right hand rule이나 left hand rule이냐 정도로 방향성 정도로 받아들이면 된다.
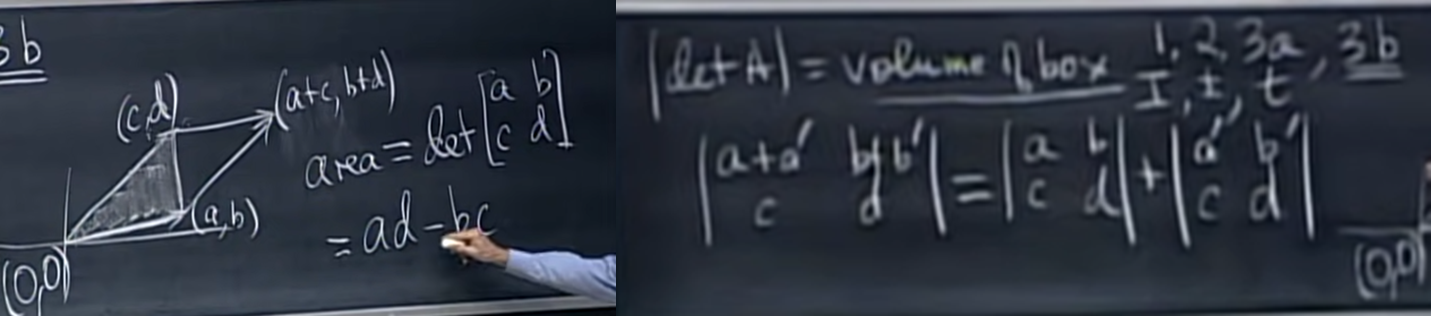
- 이렇게 determinant를 volume으로 바라보는 시선이 의미가 있는 이유는 공학적으로 연산을 단순화할 수 있는 아이디어이기 때문이다.
- 가령 예를 들어 위와 같이 (a,b), (c,d) 마름모의 넓이를 구하고 싶을 때, 일반적이라면 밑변과 높이를 찾아 곱하는 방식을 택할텐데 이러면 sqrt가 필요할 수 있다.
- 하지만 determinant == volume이라는 아이디어에서 착안하여 (a,b) (c,d)를 행렬화하고 determinant를 구하는 방식을 택하면 공학적으로 비싼 sqrt 없이 계산을 완료할 수 있다.
- 게다가 우측과 같이 (a+a', b+b') (c, d) 의 경우, 도형적으로 이해하기 어려운데 determinant를 활용할 경우 아주 단순하게 풀 수 있다.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 22. Diagonalization and powers of A (0) | 2023.01.28 |
|---|---|
| [Linear algebra] 21. Eigenvalues and eigenvectors (0) | 2023.01.28 |
| [Linear algebra] 19. Determinant formulas and cofactors (0) | 2023.01.25 |
| [Linear algebra] 18. Properties of determinants (0) | 2023.01.25 |
| [Linear algebra] 17. Orthogonal matrices and Gram-Schmidt (0) | 2023.01.21 |