[Linear algebra] 17. Orthogonal matrices and Gram-Schmidt

Lecture

https://ocw.mit.edu/courses/18-06-linear-algebra-spring-2010/resources/lecture-17-orthogonal-matrices-and-gram-schmidt/

Lecture 17: Orthogonal matrices and Gram-Schmidt | Linear Algebra | Mathematics | MIT OpenCourseWare

 

Note

• Orthonormal 단어 중 Ortho-는 서로 dot product 결과가 0이 되는 수직한 상태를 말하며, -normal은 단위 벡터임을 말한다.
• Orthonormal vector가 중요한 이유는 linear algebra를 numerical하게 풀 때 웬만하면 orthonormal vector를 이용해서 풀 정도로 문제를 단순화해주기 때문이다. 
• 대표적인 예로 우측과 같이 A.TA 형태를 자주 다루는데 그 값이 identity matrix가 나오는 특징이 있다.
• Orthonormal vector로 구성된 matrix를 orthogonal matrix라고 부른다. 
  
  

• Orthogonal matrix가 square form일 경우, 위와 같은 Q.T=Q.inv 라는 특징을 갖는다.
  
  

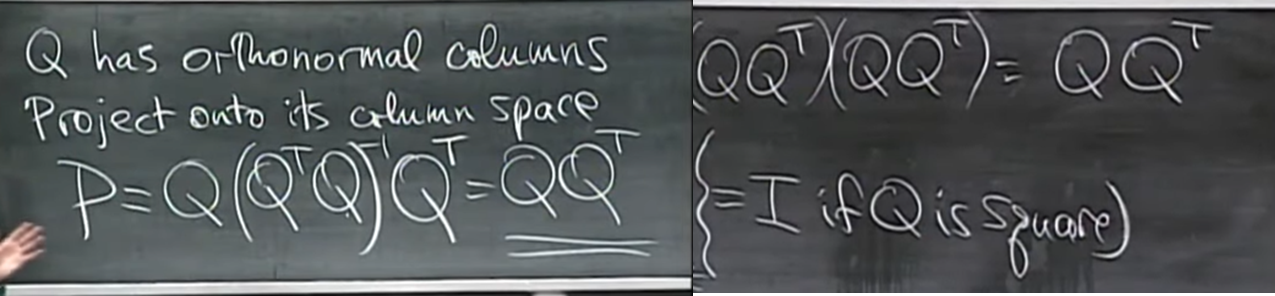
• Orthogonal matrix를 이용하면 projection matrix에서 inverse 연산이 사라진다. 따라서 연산히 간단해 진다.
• 심지어 Q가 square matrix일 경우, P=I 가 되어 연산이 필요없다. 
• A.TAx' = A.Tb 라는 least square method가 x'=Q.Tb 가 되어버린다.
  
  

• Gram-Schmidt method는 일반 벡터를 orthonormal vector로 정리하는 방법이라고 볼 수 있다. 
• 위 그림과 같이 일반 벡터 a, b가 있을 때, orthonormal vector q1, q2로 변환하는 과정이다. 
• 단순하게 컨셉을 projection matrix 설명 시 등장했던 error vector를 찾아내는 것과 같다. 수평 성분을 제거해주는 작업을 반복한다. 
• 만약 위 예시에서 a, b가 아닌 a, b, c가 존재한다면 C = c- p(a, c) - p(b, c)가 될 것이다. p()는 projection이다. 
  
  

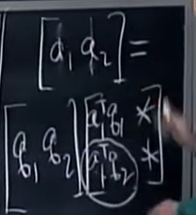
• A의 column vector를 orthonormal vector로 변환하는 방법을 알았다고 한들 A != Q이다. 
• 실제로 사용을 하면 A=QR 과 같은 형태로 우측에 matrix가 곱해진 부산물을 얻는다. 
• R 은 upper triangular matrix로 그 이유는 a1 = q1 이므로 a1.T qn = 0가 보장되기 때문이다.
• QR decomposition이라고 불리는 작업이 이것과 동일하다.