반응형
내 맘대로 Introduction
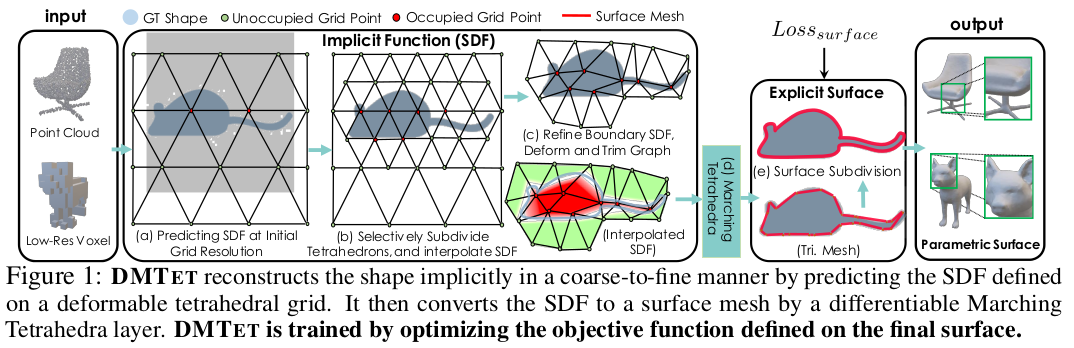
2021년 논문으로 시간이 좀 지난 논문이지만 좋은 컨셉이고 후속 연구가 없다는 것이 아쉬운 논문. 주어진 3D 입력 (pointcloud 혹은 voxel)을 일종의 query로 생각하고 tetrahederon으로 구성된 3D volumd grid를 이에 맞춰 변형하는 논문이다. 쉽게 말해 정사면체로 구성된 큐브를 구겨서 주어진 입력에 맞도록 변형하는 논문이다.
핵심 아이디어는 grid를 cube로 나누지 않고 tetrahedron으로 구성해서 marching tetradera 컨셉을 녹여내 복잡도를 확 낮추었다는 것. end-to-end라기 보다 중간중간 rule-based로 정리해주고 inference하는 것을 반복한다.
하나 노트는, 입력에 정확하게 최적화 방식으로 끼워맞추는 것이 아니고 Network에게 학습시킨 generative 모델이기 때문에 입력과 완벽하게 일치 않을 수 있음.
메모
 |
1) unit cube grid를 tetrahedron으로 쪼갬 2) tetrahedron vertex마다 sdf를 예측하는 방식 3) sdf 추정 완료 후 marching tetrahedra 수행 (surface 찾기) 4) surface 주변 tetrahedron만 subidivion 5) vertex residual + sdf residual 다시 추정. |
 |
익숙치 않지만 정사면체는 기존 triangle과 크게 다르지 않다. vertex 가 4개가 됐다는 것 뿐. ---------- subdivision도 쉽다. 각 triangle을 subdivision하고 중점끼리 연결해주면 됨. |
 |
marching tetrahedra ------- marching cube 대비 자유도가 훨씬 낮다. cube는 vertex가 8개기 때문에 각 vertex 별로 in-out을 확인해보면 총 256개 경우의 수가 있다. 256의 경우를 rotateion/symmetry를 따져서 줄여도 15개나 된다. 하지만 정사면체를 쓰는 경우 경우의 수가 애초에 16개 (2^4)로 줄고 isometric하게 줄이도 3개까지 준다. 따라서 계산 table이 굉장히 가볍다. |
 |
MT 후에 mesh를 얻고 끝내도 되지만 조금 더 표현력 좋은 mesh를 위해 MT 결과로 나온 mesh를 입력으로 받아 Graph convolution 처리 -> per-vertex subdivision weight를 찾아줌 이게 클 경우 surface subdivision 해서 mesh 해상도를 높여줌. + vertex residual까지 찾아서 최후 보정 |
 |
|
  |
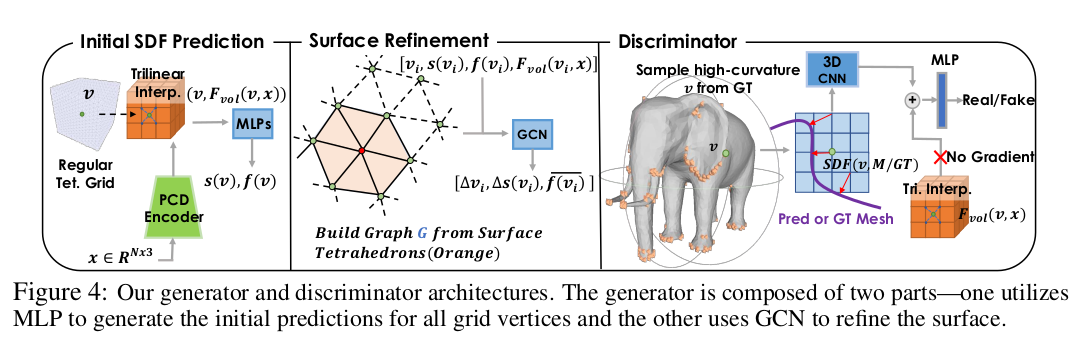
1) 3D tetrahedra grid + 3D pointcloud 입력 2) MLP가 per-vertex sdf, feature 뽑아줌 3) Graph convolution 돌려서 vertex, sdf residual 계산해서 한 번 업데이트 4) MT 수행 5) surface에 해당하는 정사면체 분류 6) subdivision (이때 SDF도 같이 subdivision) 7) MT 다시 수행 (grid resolution이 높아진 채 다시 수행하니까 mesh 품질 향상됨) 8) MT 후 얻은 mesh에 GCN 적용 -> per-vertex residual + subdivision weight 계산 |
 |
+@) 이거로도 부족했는지 3D NxNxN volume을 입력으로 받는 3D discriminator를 붙여서 학습 loss를 보충해줬음. |
 |
1) MT 수행한 결과로 얻은 vertex set이 있을텐데 이걸 3D 입력과 chamfer distance loss chamfer distance 계산시 매칭된 pair에 대해 normal도 같도록 비교 2) 3D discriminator가 붙었으므로 adversarial loss 3) 3D 입력이 Mesh로부터 만들어진 경우 GT mesh로 계산한 실제 SDF를 직접 supervision에 사용해줌. |
  |
 |
 |
 |
 |
 |
반응형