반응형
Lecture
Lecture 5: Transposes, permutations, spaces R^n | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note

- Rectangular matrix는 transpose matrix와 곱해졌을 때 symmetric matrix가 된다.
- (R.T * R).T = R.t * R, 곱해진 형태의 transpose는 앞뒤 순서 바꾸면서 각을 transpose 한 것과 같다.

- subspace란 특정 차원에 존재하는 vector로 만들 수 있는 공간 중에 합과 곱에 닫힌 형태의 공간을 말한다. (닫힌 형태란 연산의 결과값도 같은 공간에 있다는 것이다.)
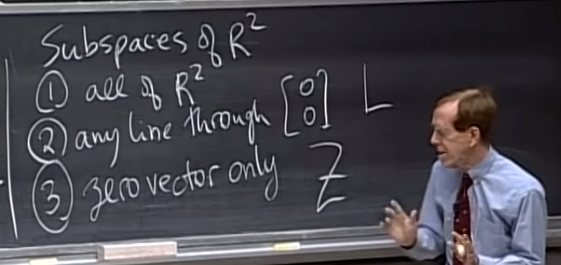
- 예를 들어, 2차원에서는 2차원 전체, 원점을 지나는 직선, 원점들이 해당한다. 원점을 지나지 않는 경우는 위 그림에서 점선과 같이 합과 곱에 닫힌 형태가 아니다.
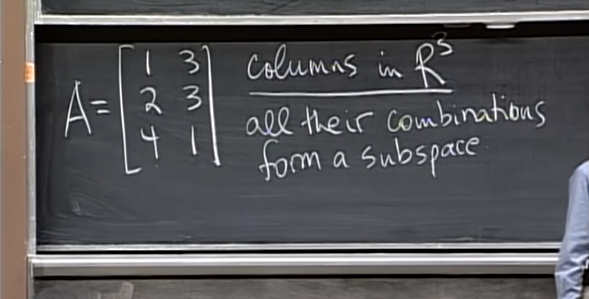
- 대표적으로 다룰 subspace 중 하나는 column vector로 구성된 column space이며 C(A)로 표기된다.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 7. Solving Ax=0, pivot variables, special solutions (0) | 2023.01.08 |
|---|---|
| [Linear algebra] 6. Column space and nullspace (0) | 2023.01.08 |
| [Linear algebra] 4. Factorization into A=LU (0) | 2023.01.05 |
| [Linear algebra] 3. Multiplication and inverse matrices (0) | 2023.01.04 |
| [Linear algebra] 2. Elimination with matrices (0) | 2023.01.03 |