반응형
Lecture
Lecture 3: Multiplication and inverse matrices | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note

- AB=C 형태의 matrix multiplication은 C의 column은 A의 column의 선형 조합이고, C의 row는 B의 row의 선형 조합으로 볼 수 있다.

- AB=C 형태의 matrix multiplication C는 위와 같이 column of A * row of B 형태로 분해할 수 있다.
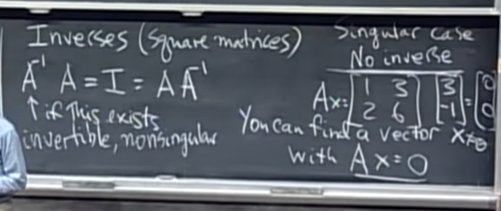
- square matrix는 right inverse가 left inverse와 동일하다. non-square matrix에서는 성립 안함. 일단 차원이 안 맞음.
- A의 inverse 존재 여부는 두가지 이미지로 확인 할 수 있다. 첫번째는 column의 선형 조합으로 0을 만들 수 있는가이고, 두번째는 row의 선형 조합으로 0을 만들 수 있는가. column의 선형조합으로 0을 만들 수 있다면 not invertible, row의 선형조합으로 0을 만들 수 있다면 not invertible이다.
- 전자는 column vector의 조합으로 1과 0을 절대 만들 수 없기 때문이고, 후자는 헷갈리는데, 만약 있다면 Ax=0의 해는 선형 조합이 가능하니 특정 x가 존재해야 하는데 수식 상 x=0인게 모순이기 때문이라고 이해하면 편할 것 같다.

- gauss-jordan method를 이용해 inverse matrix를 손으로 계산할 수 있다. [A|I] 형태의 augmented matrix를 구성하고 A의 elimination을 진행한다. 마지막 pivot까지 진행했을 경우, 역방향으로 한 번 더 진행한다. 그럼 identity matrix가 얻어지는데 이 같은 과정을 겪은 우측 I의 최종 형태가 A의 inverse이다.
- 즉, A의 inverse는 사용된 (elimination) elementary matrix의 곱이다.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 6. Column space and nullspace (0) | 2023.01.08 |
|---|---|
| [Linear algebra] 5. Transposes, permutations, spaces (0) | 2023.01.06 |
| [Linear algebra] 4. Factorization into A=LU (0) | 2023.01.05 |
| [Linear algebra] 2. Elimination with matrices (0) | 2023.01.03 |
| [Linear algebra] 1. The geometry of linear equations (1) | 2023.01.03 |