Denoising Diffusion Probabilistic Models

내 맘대로 Introduction
이 논문은 요새 뜨거운 감자인 diffusion model을 처음으로 알렸다고 해도 과언이 아닐 정도로 기념비적인 논문이다. 이전에 2015년 diffusion model 개념을 처음 소개한 논문은 따로 있지만 실제 GAN에 대적하는 성능을 보인다고 주장하여 그 우수성을 입증한 것은 이 논문이기 때문에 더 유명하다.
GAN처럼 likely-hood method를 사용하는 generative model의 일종이지만 기존에 GAN이 갖고 있는 mode collapse, 학습 불안정성, 다양성 부족과 같은 문제를 풀 수 있는 새로운 프레임워크인 diffusion model을 상세히 소개한다.
이 글은 diffusion model을 수학적으로 이해하는 것보다 직관적으로 이해하는 것을 목표로 작성했다.
배경 지식
diffusion model을 이해하기 위해선 일단 GAN을 비롯한 generative model의 역사와 이론을 알면 당연히 좋다. 일단 그것은 필수적이니 알고 있다고 치고 이외에 필요한 배경 지식이 하나 있는데 바로 Markov chain이다.
Markov chain
마르코프 연쇄는 시간에 따른 계의 상태의 변화를 나타낸다. 매 시간마다 계는 상태를 바꾸거나 같은 상태를 유지한다. 상태의 변화를 전이라 한다. 마르코프 성질은 과거와 현재 상태가 주어졌을 때의 미래 상태의 조건부 확률 분포가 과거 상태와는 독립적으로 현재 상태에 의해서만 결정된다는 것을 뜻한다.
사전적 정의는 무슨 뜻인지도 모르게 적혀있다. 전부 다 이해하려고 할 필요까지는 없고 기억해야 할 점은 "특정 상태의 확률은 오직 과거의 상태에 의존한다" 라고 가정한다는 뜻이라는 것이다.
이해를 돕기 위해 날씨를 Markov chain이 적용되는 대상이라고 가정하고 설명하면 다음과 같다.

어제 날씨를 알면 무조건 오늘 날씨의 확률을 확정적으로 알 수 있다고 가정한다. 즉, 오늘 비가 오면 내일 비가 올 확률은 60%, 맑을 확률은 10%, 흐릴 확률은 30%로 확정된다고 보는 것이다. 실제로는 여러 다른 파라미터들이 개입해서 그렇지 않지만 Markov chain이라고 가정하면 이렇게 되는 것이다.
이렇게 가정함으로써 얻을 수 있는 장점은 오늘 뿐만 아니라, 내일, 모레, 글피 그리고 많은 시간이 흐른 후의 날씨도 확률적으로 추측할 수 있게 된다는 것이다.

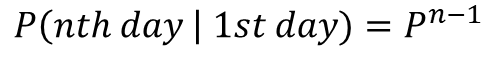
어제 날씨를 알 때, 내일 날씨를 알고 싶다면 위의 P matrix를 두 번 곱하면 된다는 것을 직관적으로 알 수 있을 것이다. 사흘 뒤는 3번, 나흘 뒤는 4번이라는 것도 당연한다.
일반화해서 말해보면 과거의 상태가 오늘 상태의 확률을 결정한다고 가정하기 때문에 시간 흐름에 따른 변화를 예측하기 쉬워진다. 그냥 확률을 계속 곱하기만 하면 되는 상태로 만들 수 있다.
(Markov chain을 가정하면 특정 시점의 상태를 계산하고자 할 때 그 이전의 확률들을 전부 곱하면 된다는 것을 꼭 기억해두자.)
핵심 내용
1. Diffusion model overview

일단 diffusion model은 gaussian noise로부터 분포를 학습해서 이미지를 생성해내는 GAN과 큰 그림에서는 똑같다. 중간 중간 가정하는 분포의 형태도 gaussian이라는 것도 동일하다. 다만 차이는 기존 방법은 일반적으로 one-stage로 noise-to-image를 한 번에 해결하려고 했다면, diffusion은 찔끔찔끔 noise-to-less noise를 반복하여 noise-to-image까지 달성하는 컨셉이라는 차이가 있다.
직관적으로도 네트워크 입장에서도 한 번에 그리라고 하는 것보다 조금씩 추측해가면서 맞춰가라고 하는 것이 더 난이도가 쉬울 것이다. 조금 더 생각해보면 이미지 분포가 gaussian이 아닌 엉뚱한 분포인데 gaussian으로 가정하는 것(noise-to-image)은 무리가 있지만 단계를 나누어 쪼개서 보면 구간 구간(noise-to-less noise)은 gaussian으로 가정해도 무리가 없을 수 있다. 다른 말로, 전체 이미지 분포를 하위 단계가 있다고 생각하고 단계 별로 잘게 쪼갠다. 그리고 상위-하위 단계 간의 차이를 gaussian 분포의 집합으로 보고 단계 별 approximation하는 컨셉이라고 할 수 있다. 더 합리적이고 approximation도 잘될 것이기 때문에 학습 안정성이 더 올라갈 것이라고 생각할 수 있다.
(내 생각이라 틀릴 수도 있다.)
2. Diffusion and reverse diffusion
Diffusion

Diffusion process는 원본이미지 x0에 noise를 더 해가는 과정이다. 이 때 diffusion process는 markov chain을 가정하고 더 noisy한 다음 상태 x1은 gaussian 형태의 확률로 noise가 x0에 더해져서 만들어진다고 가정한다. 위 그림에서 아래 녹색 흐름을 보면 된다.
이 때 gaussian noise가 들어갈 때 β를 이용해 그 정도를 조절하곤 하는데 이것은 정답이 없는 값이기 때문에 learning에 맡기거나 사람이 heuristic하게 설정한다. (논문에서는 사람이 고정한다.)
markov chain을 가정했기 때문에 특정 stage T의 분포를 알고 싶다면 그 이전의 확률을 누적 곱셈하면 된다. (위 배경 지식에서 기억하라고 한 부분이다.)

그림으로 다시 그려보면 위와 같은 것이다. 그림으로 그리다 보니 행렬처럼 되었는데 행렬이라고 보지 말고 그냥 확률 분포에 따라 noise를 더하는 연산이라고 생각하면 될 것 같다.
최종적으로 T 번 충분히 반복하면 마지막에는 결국 gaussian noise, N(0,1)만 남게 된다. 커피(이미지)에 물(노이즈)을 무한히 타면 결국 나중에 맑은 물(노이즈)가 된다는 것으로 생각하면 된다.
Reverse diffusion
이제 중요한 reverse diffusion이다. noise를 섞는 것은 사실 망치는 일이니까 아무 의미가 없다. 의미가 있는 것은 망쳐진 이미지로부터 덜 망쳐진 이미지를 복원해내는 것이기 때문에 denoise이다. 그리고 이 denoise를 어떻게 하는지 네트워크가 학습을 함으로써 결과적으로 이미지 생성을 어떻게 하는지 배우게 되는 것이다.
여기서 중요하게 알아야 할 내용은, denoise 과정에서 noise를 없앨 것인데 이 때 이 noise를 없애는 것도 gaussian 형태의 확률로 없애면 된다는 사실이다.
이해를 돕기 위해 직관적으로 상상해보면, 어제 비 왔을 때 비/맑음/흐림/등등 다양한 오늘 날씨 확률이 gaussian이었다고 치자. 그럼 반대로 오늘 날씨만 아는 사람이 이 확률 분포를 안 상태로 어제 날씨를 추측해본다고 했을 때, 어제의 날씨도 오늘의 날씨 기반 gaussian 형태의 확률을 가질 것 같지 않은가? 정확한 건 계산을 해봐야겠지만 대충 생각했을 때 gaussian을 갖는다. (이건 markov chain 이산 확률 분포를 수학적으로 더 파고 들면 그 증명이 있다고는 하는데 보지 않았다.)
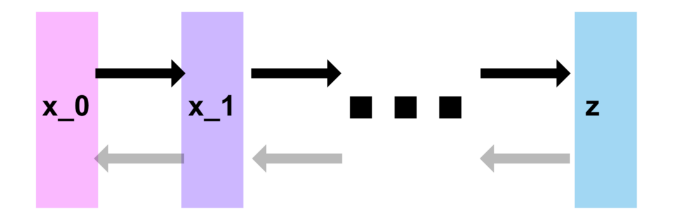
다른 말로 위 그림에서 diffusion process q가 gaussian 형태라면, reverse diffusion process p 역시 gaussian 형태로 가정할 수 있다. 근데 이 때 어떤 정도를 갖고 있는지는 모른다! (β는 확실히 아닐 것이다.) 그리고 역시나 markov chain이라고 가정할 수도 있다.
reverse diffusion process도 diffusion process처럼 간단하게 표현이 가능해지는 것이다. (markov chain을 가정하고 출발해서)
* reverse diffusion process도 markov chain이라는 점은 구현 측면에서도 의미가 있으므로 중요하다. p(x)는 neural network로 구현이 될텐데, p(x)의 누적이 단순히 곱셈으로 표현이 가능하다는 것은 neural network를 그냥 연결하기만 하면 된다는 구현적 장점이 있다. 다른 말로 reverse diffusion step마다 neural network를 따로 둘 것이라면 그 여러 neural network을 연결하기만 하면 되고, 하나의 neural network로 모든 reverse diffusion step을 커버한다고 하면 그냥 iterative call을 해주면 된다. 특별한 구현이 필요가 없어진다.

위 사진에서 diffusion process에서 β 역할을 reverse diffusion process에서 담당할 "?" 를 알아낸다면 우리는 approximation된 형태로 noise가 제거된 이미지를 복원해낼 수 있고 이것을 T번 반복하면 원본 이미지까지 거의 복원할 수 있는 것이다.
3. Training
그럼 여기서 reverse diffusion 과정에서 어떤 gaussian noise를 제거하면 되는지 그 gaussian noise의 mean, std를 어떻게 찾는가?
이건 기존 likely-hood method에서 사용한 수식을 그대로 가져와 이론 전개를 하는 과정에서 찾을 수 있다.
(이론적 내용까지 전부 알진 못해서 이 부분은 논리적 점프를 했다. 그렇구나 하고 넘어가면 되겠다. 자세한 건 generative model 역사를 공부하면서 무슨 이론을 사용하는지 살펴보길 추천)


틀린 내용
결론만 말하면, reverse diffusion process의 매 스텝의 gaussian noise는 대응되는 위치까지 diffusion process에서 누적된 gaussian noise와 같으면 된다. 이해를 돕기 위해 내가 표현한 식은 다음과 같다. (틀렸을 수도! 틀렸다.)
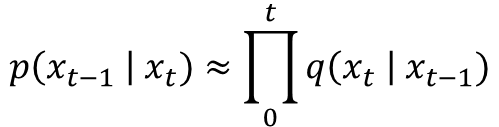
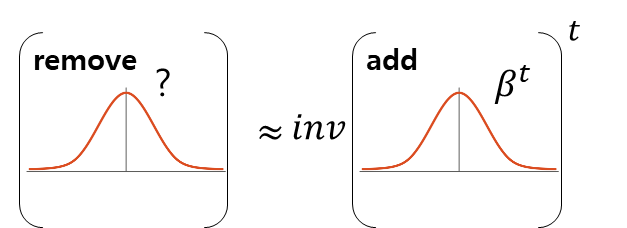
직관적으로 누적된 noise들의 비슷한 분포여야 상쇄해줄 수 있다는 느낌으로 약간 inverse니까 비슷해야 한다라고 이해하면 될 듯? (나는 이렇게 이해했다. 행렬에서 inverse로 보면 안된다.)
쉽게 말해서 내가 4번 noisy해진 이미지에서 3번 noisy 해진 이미지로 reverse diffusion을 하고자 한다면 이 때 제거해야 하는 noise는 원본에서 3번 noisy한 이미지를 만들 때까지 누적된 noise와 같다고 본다.
여기서 원본에서 3번 noisy한 이미지를 만들 때까지 누적된 noise는 3번의 gaussian 분포의 곱 (markov chain이니까) 인데 그 결과도 gaussian 분포다! (위 식에서 alpha를 사용해서 정리가 되는 이유다.)
즉, 한 시점 t에 대해서 대응되는 p (gaussian) 와 누적 q(gaussian)가 같도록 KL divergence로 학습하면 된다는 뜻이다.
정정
누적 q가 아니라 한 time, t에 대해서 reverse q, 즉 q( t-1 | t) 과 p( t-1 | t)가 갖도록 한다. noise를 더한 만큼 없앤다고 보면 된다. 한 스텝, 한 스텝마다 reverse(forward) == backward 가 되도록 학습한다. forward 시 gaussian의 중심도 움직이고 noise도 움직이는데 딱 "이만큼" 다시 돌아가도록 만드는 mu, std gaussian을 예측하도록 하는 것이다.

여기서 호재가 하나 있다. gaussian 분포를 표현하는 파라미터는 mean과 std 2개인데, 저자들이 해보니 실험적으로 std는 고정값을 사용해도 전혀 성능에 문제가 없어서 mean만 추정하도록 해도 된다는 것이다.
따라서 복잡하게 KL divergence로 loss function을 구현할 필요없이 p의 mean과 누적 q의 mean으로 loss를 구하면 된다.

여기서 호재가 하나 더 있다. 대상이 mean이 되어버린 순간 식 정리를 더 할 수 있다.
diffusion process가 전부 gaussian 형태를 가정하고 그 정도를 β로 조절하는 형태였기 때문에 ϵ ∼ N (0, 1)라는 변수를 하나 정의하면 이를 이용해서 식의 정리 (reparameterization)가 가능하다. (상세 내용이 궁금하면 supplementary를 참조)

최종적으로 위 (14)와 같이 극단적으로 단순화된 형태까지 줄일 수 있고 이를 loss function으로 쓰면 된다.
4. Tip

구현할 때 마지막 reverse diffusion step은 원본 이미지에 맞닿아있기 때문에 float 형태면 문제가 된다. 원본 이미지는 unsigned int 8 bit로 0~255로 표현된 이미지기 때문이다. 따라서 이 형식 차이를 맞춰주기 위해서 마지막 reverse diffusion step은 특별한 형태를 띄고 있어야 한다.
unsigned int 8bit의 간격 크기인 1/255 만큼씩을 묶어서 적분함으로써 강제로 continuous value를 discrete value로 변환해주는 것이다.
5. Result


잘된다... GAN 대비 성능 뿐만 아니라 학습 안정성까지 증가했다는 것을 보여준다.
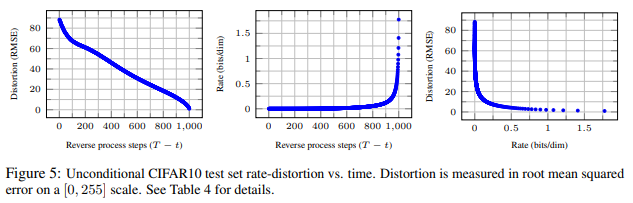
결과 중 주의 깊게 봐야할 것은 process step에 따른 네트워크의 학습 양상인 것 같다. 맨 왼쪽 그래프는 reverse diffusion을 많이 반복할수록 원본 이미지와 차이가 줄어든다는 그래프로 우하향하는 것은 당연한 결과다.
눈에 띄는 것은 중간 그래프와 마지막 그래프인데, bit는 KL divergence에서 분포 간의 다름을 의미하는 척도다. 정확히 같다/다르다를 정량 측정하는 것은 아니고 대충 분포를 같게 만들기 위해 노력하고 있는 양으로 생각하면 되겠다.
reverse diffusion 초반부에는 생성 이미지가 원본 이미지와 거의 정해진 bit로 맞춰져가다가 후반부가 되면 급증하는 bit로 맞춰져가는 것을 볼 수 있다. 이와 동시에 마지막 그래프를 보면 정해진 bit로 생성 이미지와 원본 이미지가 맞춰져 가는 시기에 폭발적으로 이미지 유사성이 증가하고 이후에는 잠잠해지는 것을 볼 수 있다.
이를 해석해보면, reverse diffusion process 초반부에는 이미지를 큰 틀에서 (semantic한 레벨에서) 먼저 맞추어 가기 때문에 bit는 적으면서도 이미지가 폭발적으로 유사해지는 것이고, 후반부에는 이미지를 작을 틀에서 (percetual한 레벨에서, 디테일 한 부분 위주로) 맞추어 가기 때문에 bit는 높으면서도 이미지는 느린 속도로 유사해지는 것이라고 볼 수 있다.
따라서 diffusion model을 semantic 정보를 먼저 복원하고, perceptual한 정보를 나중에 복원하는 형태로 신기하게 학습한다는 것도 알게 되었다.
6. Conclusion
generative model 관련된 배경 지식이 짧아서 논리적 구멍이 있을 것 같다. 그래도 직관적 이해에 도움이 됐길!