내 맘대로 Introduction

세상엔 똑똑한 사람이 많구나. Neural Implicit Surface Evolution 에서 level-set equation으로 implicit sdf function 간의 interpolation을 GT없이 전개한 것에 감탄하고 수학적 깊이에 후속 연구가 나오긴 시간이 꽤 걸리겠다 싶었는데, 단번에 이 논문의 단점을 지적하면서 개선한 논문이 나왔다. shape matching을 파고드는 뚝심있는 연구실에서 나온 논문이라서 이 역시 수학적 깊이가 남다르다. 역시 내가 모른다고 남도 모르는게 아니다.
이 논문은 기존 implicit function g1, g2 간의 interpolation을 풀 때 가장 문제가 됐던, point tracking이 안된다는 점 + 중간 변화 과정에서 surface regularization까지는 못한다는 점이다. SDF 공간 자체에 초점을 두기 때문에 geometric constraint를 추가하지 못했다는 점을 지적했다. 그래서 입력이 point cloud이고 계속 surface point만 입력으로 두면서 푼다. on-off surface point를 샘플링하는 것이 아닌 surface point, 즉, vertex만 입력으로 넣는 구조로 바꾸어서 트래킹이 가능하도록 고정했고 이와중에 SDF도 같이 학습되도록 했다.
더불어서 NISE의 경우, interpolation 대상이 되는 두 형상에 대해 initial implicit function을 사전학습 해두어야 하는데 이 논문은 그런 것 없이 end-to-end라서 편의성이 크다. 단점이라 함은 NISE 대비 sparse correspondence GT 확보를 필요로 한다는 점. 1% 정도는 correspondence를 알고 있어야 된다. (이 부분이 엄청 큰 단점인 것 같긴 하다.)
메모
 |
SDFnet, f 를 쓰는 표현법이 굉장히 파워풀한 것은 맞지만 1) point 렙레의 tracking이나 manipulation이 쉽지 않음. (implcit니까 당연히) 2) neightbor 정의가 쉽지 않아서 geometric constraint를 걸기가 쉽지 않음 크게 두가지 문제가 도드라진다. |
 |
NISE가 level-set equation을 갖고 2)에 대한 문제를 완화하는 듯 했으나 아쉬움이 있다. ( 1)은 여전히 남아있음) NISE에서는 interpolation 중간에 가해지는 vector field를 SDF를 갖고 계산한 수식으로 고정해두고 사용한다. 이게 효과적이긴 하지만, 좀 더 섬세한 vector field 디자인이 있다면 개선될 여지가 있다고 지적함. ->이 논문에서는 neural net으로 대체 |
 |
일단 1)의 문제를 해결하기 위해서 문제를 바라보는 관점은 eulerian 에서 lagrangian으로 바꾼다. 쉽게 말해서 공간을 기준으로 보던 시각 ( 공간 내 x를 sampling)에서 입자를 기준으로 보는 시간 (공간 내 pointcloud sampling)으로 바꿨다. point 개별적으로 particle로 다루는 관점으로 바꾸면서 tracking은 자연스럽게 해결된다. (sampling을 vertex만 함) 두번째로 2)의 문제를 해결하기 위해서 vector field에 constraint를 추가한다. 역시나 implicit representation을 학습 과정에 사용하므로 neighbor 개념 정의부터 geometri constraint를 부여하는 것은 어렵다. levelset equation과 더불어 간접적으로 형상 변형을 유발하는 vector field가 형상의 부피를 유지하도록 한다는 조건을 추가해준다. |
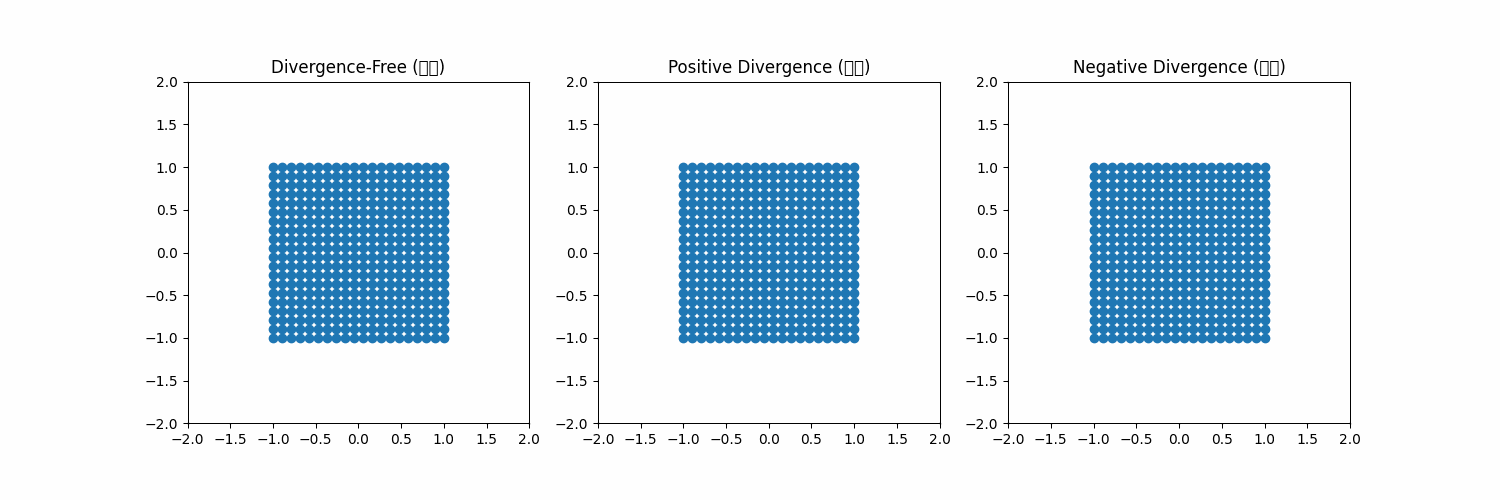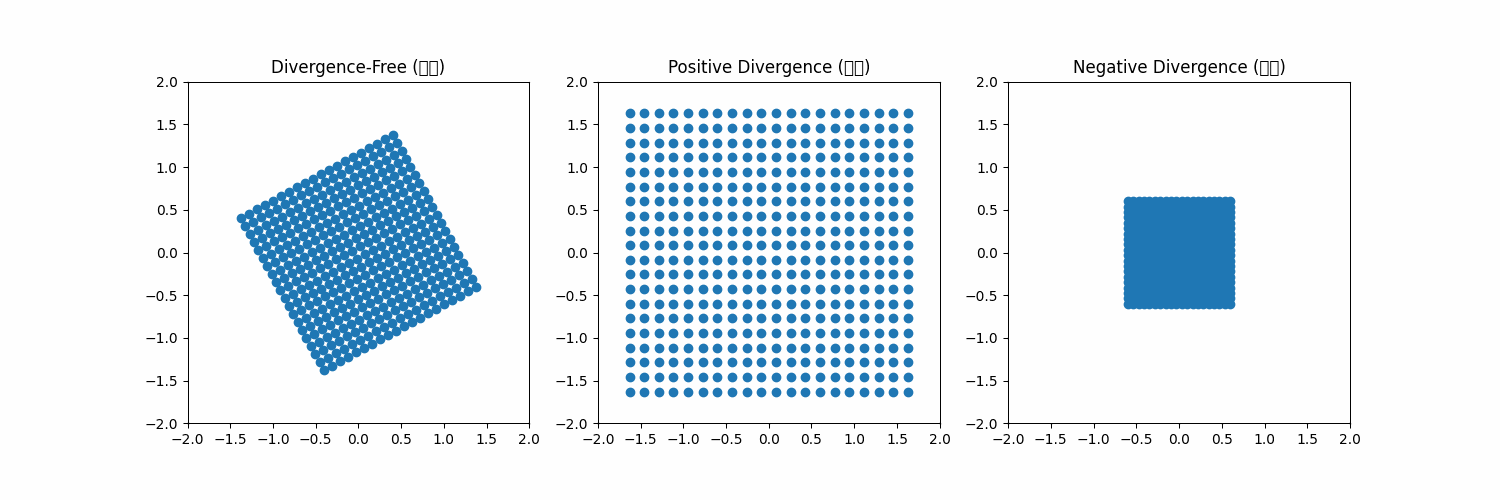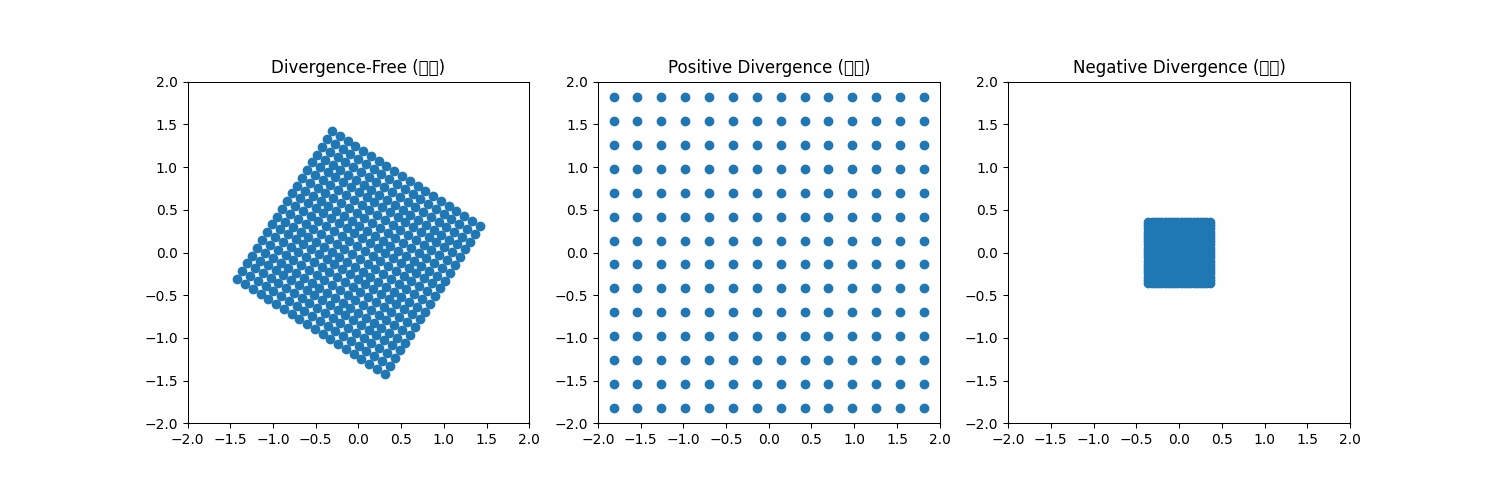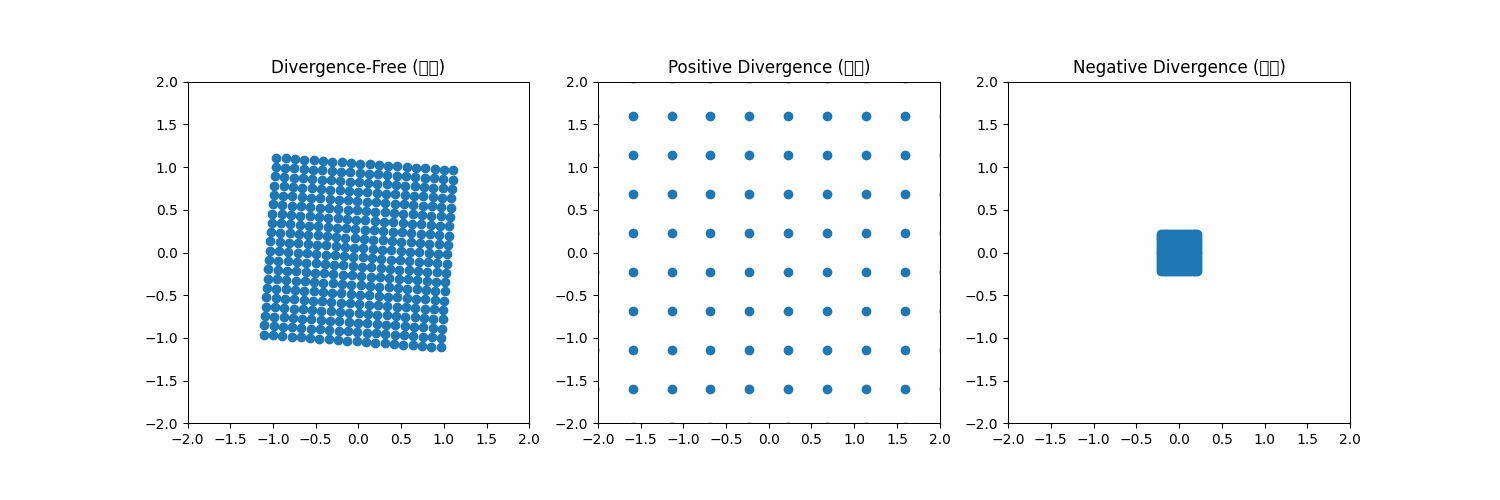 |
2)에서 말하는 divergence-free constraint는 좌측에 내가 그린 예시 그림으로 보면 이해하기 쉽다. vector field가 공간에 존재하면 그 안에 particle의 변형/이동을 유발하는데 첫번째 처럼 주어진 공간을 particle들이 벗어나지 않게 하는 벡터장이 있고, 두번째 세번째처럼 공간에서 이탈하거나 수렴해서 사라져버리도록 만드는 벡터장이 있을 수 있다. 2, 3번째의 경우, 시간이 흐를수록 공간 안에 particle이 사라지기 때문에 particle을 geometry를 구성하는 vertex라고 본다면, regularization을 어떻게 해주더라도 벡터장이 저모양으로 생겼으면 형상이 무한히 팽창해버리거나 구겨져서 점이 돼버린다. 따라서 벡터장이 공간 안의 particle을 공간 안에 머물도록 하는 조건이 최소로 만족되어야 형상 변화 시 질량 보존 법칙을 따를 수 있게 할 수 있다. |
  |
구체적인 방법은 NISE과 같이 position x와 함께 time step t를 입력으로 받는 implicit fuction, f를 학습시키는 것이다. SDF function이기 때문에 eikonal equation이나 gradient가 normal을 따른다는 조건, 곡률 계산이 용이하다는 점 등을 그대로 활용할 수 있다. 다시 말해 기존 framework에서 vector field를 수정하고, regularization을 추가한 것. |
 |
벡터장은 형상을 변형시키는 외력과 같은 것인데 공간 안에 존재하고, static하다. 시간에 따라 변하지 않는다. 따라서 단순히 point의 위치 변화율이 벡터장을 의미한다. 개념상 point의 위치 변화율 -> 해당 위치 vector 장의 크기/방향을 알 수 있음. |
 |
벡터장은 sdf 의 미분값으로 사용할 수도 있지만 여기서는 velocity net이라는 MLP를 붙여서 사용했다. 단순 모델링을 넘어서 nonlinear 모델링 능력을 부여하기 위함이다. 이 값은 network 예측값이기 때문에 억제가 필요한데 벡터장이 주변 대비 smooth하도록 억제해준다. 이 때 vertex가 쿼리 x로 들어가기 때문에 neighbor vector를 계산할 수 있고 neighbor vector 간의 laplacian이 0이 되도록 어게하는 것이다. |
 |
추가로 벡터장이 div가 0이 되도록 함. div(V)가 0이라는 뜻은 위에 gif 예시에서 본 것처럼 공간을 벗어나지 않게 하는 벡터장으로 억제한다는 것. 질량 보존을 따르도록 하는 힘. |
 |
개념상 point의 위치변화율로 계산한 벡터장과 MLP로 예측한 벡터장 간의 등식이 성립하지 않는다면 따로 국밥이기 때문에 애초에 수식이 성립하지 않는다. 따라서 수식(8)과 같이 걸어주는 것은 필수 |
 |
이제 벡터장에 대한 새로운 정의 + constraint를 추가한 부분은 끝났다. 핵심이 되는 level-set equation 부분을 손댈 차례 LSE는 수식(10)으로 이미 밝혀져 있다. 하지만 저 수식을 만족 해야만 하지만 저 수식으로만 최적화를 돌려 보면 학습을 거듭할 수록 f가 더 이상 sdf function이 아니게 된다. 저 수식을 만족하도록 f가 수렴하지만 f가 물리적으로 SDF 값을 내뱉는 함수가 아니게 된다. (필요조건 같은 느낌, 충분 조건이 아니라서 최적화를 완벽하게 돕진 않음) ---- 그걸 해결하는 방법이 수식 (11) 학습 중간 중간마다 홀드한 상태에서 새로운 시간 축에 대해서 최적화를 한 번 돌려주면서 가야한다. (기존에 학습하던 시간이 아니라 새로운 가상의 시간 방향으로 한번 또 다른 최적화를 돌려주는 것) |
 |
하지만 학습 중간중간마다 멈춰서 돌려야 된다는 단점 + 이미 학습 과정에서 gradient를 계산해서 푸는 PDE가 껴있는데 또 다른 PDE를 풀어야 한다는 점에서 graph를 끊었다 재초기화하는 것이 엄청난 비효율을 불러일으킴. 따라서 이 방식을 채택할 순 없고, 학습 과정에서 수식(11)이 발생시키는 효과와 유사하도록 regularization을 추가해주는 방향으로 우회한다 ---- 그 결론은 modified LSE라고 어떤 수학 논문에서 수식(12)와 같이 distance fuction이 찌그러지는 방향을 계산해서 보정해주는 term을 우변에 넣어준다. 이게 이상적으로는 0이 나와야 하기 때문에 우변에 더해준다고 해서 기존 LSE를 무너뜨리는 것은 아니다. 최적화 과정에서 보상해야 되는 값이 발생했을 때만 우변에 억제하는 힘이 발생하는 것. (자세한 증명은 모르겠다. 출처 논문을 읽는 것 까지는 포기함) |
  |
최종 정리하면 벡터장이 smooth 하도록 억제 벡터장의 div가 0이 되도록 해서 질량보존 Modified LSE로 implicit function이 smooth 변형을 유도 initial condition으로 주어진 point cloud에 대해서 sdf가 0이 되도록 유지 마지막으로 주어진 sparse correspondence에 직접 supervision ---------- 마지막에 들어간 sparse supervision이 어떻게 보면 핵심이 되고 나머지는 전부 강한 regularization 이므로 필수적이다. 저자들도 이 correspondence를 이미 알고 있는 데이터 필요성을 큰 단점으로 인식했는지 얼만큼 줄일 수 있는 분석한 걸 추가해뒀다. |
 질량 보존 항과 꾸겨짐을 보상하는 항의 추가로 조금 더 부드러운 변형이 됨. |
 |
 start 와 end만 주어진 환경에서 중간 값을 요동칠 수 있는데, 중간 예측값의 안정성을 보면 다른 논문 대비 훨씬 잘 regularization 되는 것을 볼 수 있다. |
 굉장히 sparse해도 잘 동작한다고 함. sparse correspondence가 주어진 상황에서 regularization 힘이 돋보임. |
 |
 이 결과는 해석하기 나름인데, 질량 보존에 기여하는 div(V)=0으로 억제하는 term을 끌 경우에는 형상이 팽창하거나, 수축 하는것에 대한 억제가 없기 때문에 수렴이 잘 되었을 때 a-to-b 과정에서 b에 fit한 결과를 얻을 수 있다. 억제를 할 경우에는 b의 형상을 잘 따라가지만 a의 부피를 벗어나지 않는 선에서 잘 따라가는 억제력이 발생함. a >> b인 상황이나 defomration이 큰 경우에는 의미가 있지만 비슷한 형상에서는 끄는 것이 오히려 도움이 될 수도 있겠다. sparse correspondence가 전체 point cloud의 1%만 제공되어도 충분히 정확하다고 한다. |
 sparse correspondence가 noisy하다면 잘 동작하는가? -> 안정성은 나온다. 다른 항들의 힘으로 |
|
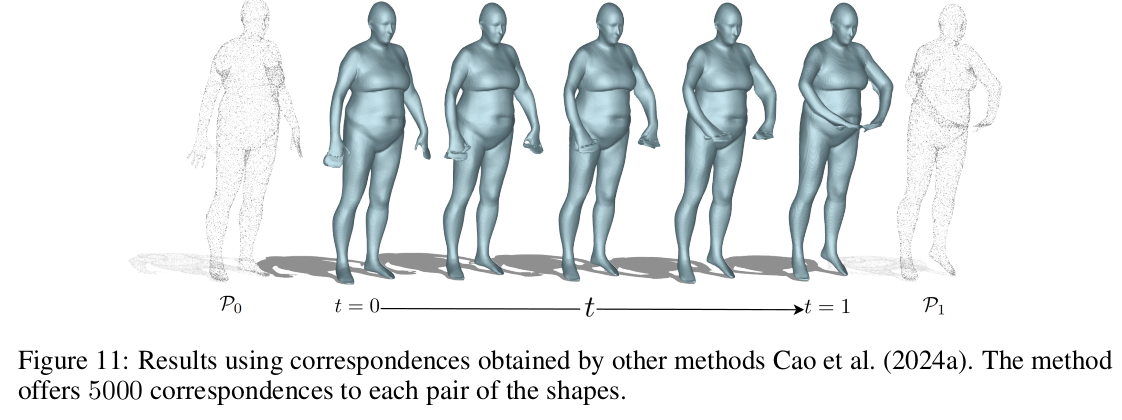 correspondence를 뱉어주는 다른 알고리즘의 입력 (noisy 입력)을 활용할 수 있음도 보여줌. |
 벡터장을 smooth하게 만드는 laplacian 억제를 안할 경우 형상이 망가짐. |
 |
'Paper > Others' 카테고리의 다른 글
| Parallel Sequence Modeling via Generalized Spatial Propagation Network (a.k.a GSPN) (0) | 2025.07.08 |
|---|---|
| 4Deform: Neural Surface Deformation for Robust Shape Interpolation (0) | 2025.06.13 |
| Neural Implicit Surface Evolution (0) | 2025.06.10 |
| Harnessing the Universal Geometry of Embeddings (0) | 2025.05.30 |
| DreamSim: Learning New Dimensions of Human Visual Similarity using Synthetic Data (0) | 2025.05.29 |