Neural Implicit Surface Evolution

내 맘대로 Introduction

 

짧고 굵은 제목에서 느껴지는 힘만큼이나 알찬 내용을 담고 있는 논문. 어떤 application을 고민한 논문이 아니라 수학적으로 implicit surface를 표현하는 function, g를 어떻게 변형할 수 있을지 고민해본 논문.

 

이미 어떤 형상의 SDF를 표현하도록 학습해둔 implicit function, g이 있다고 했을 때 우리는 그대로 쓰는 것 밖에 못한다. implicit function이 아닌 mesh 표현법을 택했다면 smoothing, simplification 등 후가공이 가능했을텐데, implicit function으로 표현한 순간 변형이 불가능하기 때문에 고정된 형상 표현법이라고 가정하곤 했다. 

 

저자들은 g가 주어졌을 때 geometry에 부합하게 f를 업데이트할 순 없을까? SDF function이 만족해야 하는 constraint를 기반으로 g를 변형할 수 있는 방법론을 탐색한게 이 논문이다. 내용이 조금 어려워서 더 직관적으로 설명을 못하겠다. 

 

논문에서는 주어진 implicit function,g가 특정 외력에 의한 변형, 형상 곡률을 따라 변형, 또 다른 g'를 향한 변형 3가지가 가능함을 보여줬다.

 

메모

우리가 SDF implicit function 같은 걸로 어떤 형상을 표현하는 방법은 NeRF, IDR, NeuS 등 radiance field 논문들이 등장하면서 흔해졌다.  3차원 vertex가 query로 주어졌을 때 이에 대응되는 SDF 값을 뱉는 구조로 R3->R1로 가는 function, g가 여기서 그 예시다.  ---- 우리 목적은 근데 학습 완료된 g의 변형이므로 시간 축이 하나가 더 필요하다.  따라서 주어진 g를 기본으로 깔고 g == f(t=0)  3차원 vertex + 시간 t 가 query로 주어졌을 때 sdf로 가는 R4->R1 구조의 f를 학습시키는 것이 본 목표다.  이 때 f에게 무한히 많은 t에 대해서 변형 중간 과정을 다 보여주면서 학습하는 것은 불가능하기 때문에 discrete한 시간을 보여주고 중간중간은 합리적으로 배울 수 있도록 억제하는 무언가를 추가한게 이 논문의 핵심.

일단 f가 SDF fucntion이니까 공간에 대한 미분, df는 법선 벡터를 의미한다는 것 (NeuS를 이해했다면 당연히 알 내용) 깔고 가야하고 f는 4D conv 같은 걸로 구현하면 메모리가 터질게 분명하고, df를 계산하기도 어려워지므로 단순히 MLP 기반 구조를 사용한다는 것도 깔고 간다.

implicit function, g의 변형, 즉 f를 학습시킬 때 f가 중구난방으로 학습하지 않도록 억제하는 억제기는 level set equation, LSE다.  시간에 따라 f가 smooth하게 변형되려면 자연스럽게 편미분 방정식을 만족해야 한다.  어떤 한 점 x가 있을 떄 얘가 변화 과정에서 그리는 경로 a(t)가 있다고 해보자. x는 변형 전이나 후나, 표면에서 떨어진 거리는 같은 것이 이상적인 것이다. 다시 말하면 원래 형상에서 크게 벗어나지 않도록 형상과 같이 움직여서 SDF가 일정하게 움직이는 것이 이상적일 것. "함수값은 시간 흐름 속에서 보존되며 변형된다" -> 이 말을 수식으로 쓰면 수식(3)과 같이 적을 수 있다.  원래는 df/dt =0 인데 f가 공간과 시간 2개의 파라미터가 있으므로 편미분 형태로 chain rule로 분해하면 수식(3)이 됨. 의미하는 건 시간에 따른 변화량이 0이라는 가정.  ----- 이 가정을 유지하도록 강제하면 f에 의해 변형이 일어나도 기존 g SDF를 최대한 유지하도록 강제된다.  ------ 예시에서 사용한 경로 alpha는 수식 상에서 a(t) == p, 로 대체되므로 a'만 사용되는데 경로의 미분값은 공간상의 변화량이므로 "특정 벡터"로 치환할 수 있다. 예를 들면, 외력, normal vector 등

위와 같이 수식(4)의 핵심 억제기 수식을 만들어 놓고 이걸 어떻게 이제 적용할까 수식(5)와 같이 억제기는 당연히 사용하고,  특정 time step에 대해 gt SDF가 있다면 추가로 사용해주면서 업데이트하면 된다.  ---- 외력에 의해 변형하는거면 g0 말고는 없을 것이고 normal에 의해 팽창이나 수축하도록 변형하는 것도 g0말고는 없음 다른 g'와 interpolation하는 변형은 g0, g1 2개 존재

억제기 수식 F는 그 크기가 0인게 이상적이므로 그냥 값 자체로 최소화하면 smooth 변형을 강제함 g가 존재할 경우 time t에 변형된 f 값이랑 g_i랑 가깝도록 최소화해주면 됨.

g_i가 존재하더라도 시작과 끝 2개나 discrete한 N개 일텐데 연속적인 t에 대해서 어떻게 학습을 시킬 수 있는가? 억제기 수식F가 중간 t에 대해서 잘 억제를 해주므로 그냥 N개로 학습해도 된다.

구체적으로 구현할 때는 공간에서 N개의 point p를 뽑고 이걸 query로 던져주면서 minibatch 학습을 한다.  부수적으로 f가 sdf function이니까 eikonal regularization을 넣어주고, div(f)가 normal하고 같도록 해주는 regularization도 추가해준다. 네트워크 구조는 앞서 MLP를 쓴다고 했는데 SIREN으로 썼다.

f는 g보다 조금 더 넓게 (깊이는 같지만 차원이 더 크다는 뜻인듯) 설계했다고 함.

V가 외력 vector일 경우, 예를 들면 머리 부분에는 압력, 몸통 부분에는 팽창하는 힘이 작용하는 vector field안에 있다고 생각해보면 됨 그러면 F에 작용했던 <div(f), a'>을 외력으로 바꿔주면 됨.  data term은 g0 초기 SDF function 밖에 없으므로 f0가 그거랑 유사하도록 하는 것 밖에 못함. 이렇게 하면 주어진 외력에서 형상이 smooth하게 변형되는 것을 볼 수 있음 물론 무한히 외력이 작용하기 때문에 계속 반복하면 형상이 깨진다.  특정 iteration에서 사람이 멈춰줘야 함.

만약 외력이 아니라 그냥 형상의 normal을 따라 조금 부풀거나 shrink하는 변형은 어떻게 할 수 있을까 형상 표면의 normal 방향으로 외력이 있다고 가정하고 mean curvature equtation으로 힘의 크기 만들어 주면 됨.

이게 내가 볼 땐 제일 핵심인데  g0와 g1가 존재할 때 둘 간의 interpolation은 어떻게 할까  point, p에 대해서 g0 g1 sdf gt가 있기 때문에 이걸 갖고 학습해주면 됨.  sdf가 거리 개념이기도 하니까 수식9와 같이 sdf간의 차이가 변형 크기를 의미할 수 있음   여기다가 div(f)를 곱해주면 방향이 생기니까 그대로 외력과 같아짐

몸통을 회전시키는 외력이 존재한다고 하면 형상 유지하면서 외력 방향대로 변형 잘되고	머리에는 압력, 몸에는 팽창하는 외력이 존재한다고 하면 위와 같이 자연스럽게 변형 잘됨.
스스로의 표면 형상을 유지하면서 변형되도록 하면 이렇게 됨	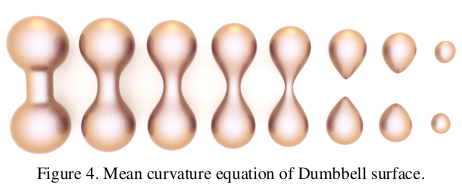어떻게 변형될지 예측은 못하지만 각 단계가 smooth하다는 것은 볼 수 있음. 자연스럽다.

이건 활용하기 나름인데 표면 형상 유지하면서 변형을 아주 조금 시키면 smoothing하는 효과를 만들어낼 수 있고

이건 트릭인데, t를 음수를 넣으면 sharpening도 노릴 수 있다.  (이건 근데 파인데를 더 파이게 하는거라 의미가 있는지는...)

mesh 기반 방식보다 형상 유지하면서 변형하는 측면에서는 강점이 있음. 단순 simplification보다 나은 측면이 있따.