반응형
Lecture
Lecture 9: Independence, basis, and dimension | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note

- column의 independence는 각 column의 linear combination으로 zero vector를 못만드는지 확인하면 된다. 전부 다 0을 곱해서 억지로 만드는 zero combination을 제외하고는 만들 수 없을 경우, 모든 column은 independent하다고 볼 수 있다.

- 2차원에서 예를 들면, 위 사진에서 v1과 v2만 있었다면 이 둘을 합쳐 0을 만들 방법은 둘 다 0배를 곱하는 방법 외에는 없다. 따라서 v1과 v2는 independent하다.
- 하지만 v3가 더해진 순간 a*v1+b*v2 = c*v3 를 무조건 만들 수 있기 때문에 dependent 해진다.
- 무조건 만들 수 있는 것이 이해가 안된다면 A matrix로 정렬해서 보면 full row rank matrix가 되기 때문에 nullspace가 반드시 존재하고, nullspace가 존재한다는 말은 zero vector 외에 0을 만들 수 있다는 것으로 봐도 된다.
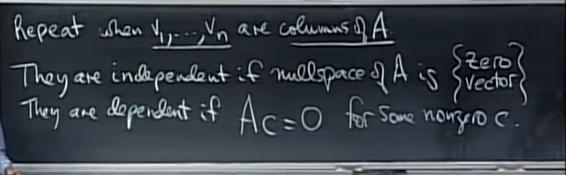
- 아예 표현을 앞서 배운 개념을 활용하여 재정립하면, matrix A의 nullspace가 zero vector 뿐일 경우 independent이고 nullspace가 따로 존재할 경우 depedent하다고 볼 수 있다.
- 즉 A가 full column rank일 경우는 independence가 보장되고 그 이외에는 dependent하다.

- 여태까지 vector가 확장돼서 space를 구성한다는 개념을 흔히 접했다. vector 들이 independent할 수도, dependent할 수도 있는데 이 모든 vector들이 생성하는 space를 생각했다.
- basis라는 개념은 반대로 space가 주어졌을 때, 이를 만들어낼 수 있는 최소의 vector는 어떤 것일까? 라는 초점에서 나왔다.
- 주어진 space에 대해 이를 구성하는 최소 vector 들을 basis라고 부른다. 이들은 각각 independent해야 하며 확장했을 때 주어진 space를 만들어낼 수 있어야 한다.
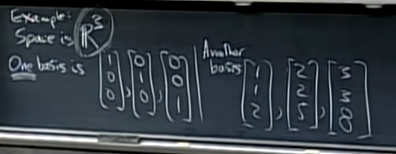
- 예를 들면, 3차원에서 [1,0,0], [0, 1, 0], [0, 0, 1]은 basis다. 이것만 존재하는 것은 아니고 [1, 1, 2] [2, 2, 5], [3, 3, 8]과 같이 다른 형태를 띌 수도 있다.
- 하지만 역시나 서로 independent하며 확장했을 때 3차원 모든 공간을 커버한다는 조건은 만족해야 한다.

- n차원 space를 이야기할 때는 n basis가 필요하다. n을 space의 dimension이라고 한다.
- 이를 matrix A (n x n) 형태로 표현했을 떄 A가 invertible해야한다고 표현할 수도 있다.
- square matrix일 때는 invertible 하면 column vector들이 basis다.
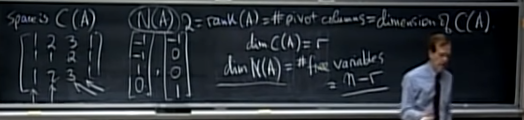
- 지금까지 쌓아온 pivot column, rank, dimension 등 개념들을 하나 묶으면 다음과 같다.
- rank(A) == # of pivot columns of A == dimension of C(A)
- 추가적으로 nullspace도 dimension이 있다. nullspace는 free variable 개수만큼 생성하는 special solution이 확장되어 만드는 공간이므로 space solution의 개수가 dimension이다.
- 즉, n - rank(A) == # of free columns of A == dimension of N(A)
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 11. Matrix spaces, rank 1, small world graphs (0) | 2023.01.13 |
|---|---|
| [Linear algebra] 10. The four fundamental subspaces (0) | 2023.01.11 |
| [Linear algebra] 8. Solving Ax=b: row reduced form R (0) | 2023.01.09 |
| [Linear algebra] 7. Solving Ax=0, pivot variables, special solutions (0) | 2023.01.08 |
| [Linear algebra] 6. Column space and nullspace (0) | 2023.01.08 |