반응형
Lecture
Lecture 10: The four fundamental subspaces | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note
- 4개의 fundamental subspace는 C(A), N(A), C(A.T), N(A.T) 이다. 이름으로는 column space, null space, row space, left null space이다. 특징점은 row에 대한 space도 transpose를 취하여 column space로 보아 표현한다는 것이다.

- m x n matrix A가 있을 때, n차원 공간에 있는 subspace는 N(A)와 C(A.T) 이며 m차원 공간에 있는 subspace는 C(A)와 N(A.T)이다.
- column space와 row space는 같은 dimension을 갖는다. 즉 rank r dimension을 갖는다. 생각해보면 rank r이 indendepent한 row의 개수를 의미하기도 하는데 이는 다른 의미로 pivot row 가 r개라는 소리고 dimension이 r이라는 소리다.
- null space는 n-r dimension, left null space는 m-r dimension이다. 이는 앞서 배운 rank와 free variable 개념을 떠올리면 직관적으로 이해된다.
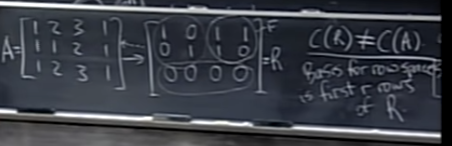
- A 와 R(reduced row echelon form)는 column space 측면에서 보면 다르다. C(A) != C(R)이다. column vector가 바뀌는 것을 볼 수 있다.
- 하지만 row space 관점에서 보면 C(A.T) == C(R.T)이다. elimination step 자체는 row 입장에서 보면 linear combination일 뿐이어서 row space 자체를 변화시키진 않는다.
- row space의 basis는 R.T의 column이다. 즉, R matrix의 각 row이다. 이게 가장 간단한 숫자들로 값이 정리된 형태다.

- left null space라는 이름 자체는 A.T*y = 0 일 때 양변에 transpose를 취했을 때 결과물 때문에 생겨났다. 위사진 참조.

- left null space를 찾는 방법은 elimination elementary matrix를 추적해야 해서 귀찮긴 하다.
- EA = R 형태로 정리할 때 발생하는 E에서 left null space basis를 찾을 수 있다.
- R의 zero row에 대응되는 E의 row가 left null space basis다. 우측에 곱해진 형태여서 찾는 방법이 다르다.

- 10강의 마무리는 여태까지 vector만 다루었던 개념이 matrix에서도 통용됨을 암시하며 마무리한다.
- matrix 또한 vector와 같이 보아 n차원을 넘어서 n x n 차원을 고려할 수 있다.
- 자세한 내용은 아마 이어지는 강의에서 나오지 않을까.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 12. Graphs, networks, incidence matrices (0) | 2023.01.13 |
|---|---|
| [Linear algebra] 11. Matrix spaces, rank 1, small world graphs (0) | 2023.01.13 |
| [Linear algebra] 9. Independence, basis, and dimension (0) | 2023.01.10 |
| [Linear algebra] 8. Solving Ax=b: row reduced form R (0) | 2023.01.09 |
| [Linear algebra] 7. Solving Ax=0, pivot variables, special solutions (0) | 2023.01.08 |