반응형
Lecture
Lecture 11: Matrix spaces; rank 1; small world graphs | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note
- vector에서 확장되어 matrix도 vector의 일종으로 바라볼 수 있다. 또 다른 vector space는 matrix space인 것이다.
- 예를 들면, 어떤 3 x 3 matrix M 이 있을 때, 이는 [1, 0, 0, ..., 0], [0, 1, 0, ..., 0] ... [0, 0, 0, ..., 1] 의 basis로 만들어진 것이라고 바라볼 수 있다.
- 단, matrix는 vector와 달리 합과 곱의 방식이 다르기 때문에 subspace를 생각할 때 몇몇 차이점이 존재한다.
- 첫번째로 scalar를 곱하는 것은 다루지만 matrix 간 곱은 다루지 않는다. 즉 3A는 있지만 AB는 고려하지 않는다.
- matrix 간의 곱은 차원의 변화도 있고 dot product 형태이기 때문에 subspace 개념을 다루기 어렵다. 그나마 곱 대신 intersection을 다룬다.
- 두번째는 합 A+B를 union이 아닌 새로 정의한 sum으로 다룬다.
- matrix A와 matrix B 사이의 union은 subspace를 보장하지 않는다. 각각이 subspace이긴 하지만 서로 다른 방향으로 정의된 subspace이기 때문에 합쳐졌을 때 subspace를 형성하지 않는다. 단 한 경우에만 subspace를 여전히 생성한다.
- 간단히 line 형태의 subspace로 상상해보면, line 두 개가 교차하는 모양이 될텐데 합과 곱에 대해서 항상 line 위에 존재해야 한다는 조건은 만족하기 어렵다.
- 따라서 union 대신 sum이라는 개념을 도입한다. 어떤 S와 어떤 U를 element-wise 더했을 때 생성되는 새로운 matrix N을 정의하고 사용한다. N은 subspace임이 보장되고 S와 U보다 더 높은 차원의 subspace다.

- 예를 들면, symmetric matrix S와 upper triangluar matrix U가 있을 때, 이는 각각 6차원, 6차원의 matrix들인데 이들의 intersection 은 3차원, sum은 9차원을 형성한다.
- intersection(S, U)는 diagonal matrix이니 3차원, sum(S, U)는 3x3 공간 전체를 채우니 9차원인 것이다.
- 아름다운 점은 dim(S) + dim(U) == dim(intersection(S,U)) + dim(sum(S,U)) 라는 점이다.

- rank1 matrix는 중요한 역할을 한다. 위 사진 예시처럼 rank 1 matrix A는 column x row 로 decomposition된다는 사실때문이다.
- 이는 나중에 m x n 의 고차원 matrix도 수많은 rank 1 matrix의 조합으로 분해할 수 있어 마치 building block과 같은 역할이다.

- building block으로 바라볼 때 알고 있어야 할 사실 중 하나는 matrix M을 구성하는 수많은 rank 1 subset matrix들은 subspace를 형성하지 않는다. 가령 rank 1 A + rank 2 B는 rank 2가 될 수 있다.
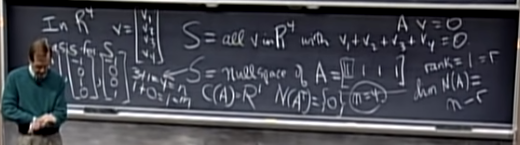
- 또, rank1 matrix의 N(A.T)={0}, C(A)=R1 이라는 사실이다.
- 위 예시는 v1+v2+v3+v4=0을 만족하는 집합 S를 해석하면 Av=0 즉 A=[1, 1, 1, 1]인 rank 1 A 문제로 볼 수 있기 때문에 등장한 것이다.
- A의 null space를 찾는 문제로 볼 수 있는데 여기서 null space만 보면 n-r 차원으로 특별한 것이 없어보인다.
- 하지만 column space와 left null space, row space를 보면 1차원, 0차원, 1차원으로 극도로 단순화된 차원임을 알 수 있다.
- 즉, rank 1 matrix는 building block으로 쓸 때 단순화 기능을 할 수 있다. (나중에 더 나올 것이라 기대 중.)

- graph 데이터 구조는 linear algebra로 분석할 수 있는 대상 중 하나라고 던지며 마무리.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 13-14. Orthogonal vectors and subspaces (0) | 2023.01.15 |
|---|---|
| [Linear algebra] 12. Graphs, networks, incidence matrices (0) | 2023.01.13 |
| [Linear algebra] 10. The four fundamental subspaces (0) | 2023.01.11 |
| [Linear algebra] 9. Independence, basis, and dimension (0) | 2023.01.10 |
| [Linear algebra] 8. Solving Ax=b: row reduced form R (0) | 2023.01.09 |