반응형
내 맘대로 Introduction

앞선 논문들의 핵심 래퍼런스 논문으로 언급된 NJF. 짱도비에서 쓴 논문답게 완성도가 대단하다. 역작 논문.
mesh to mesh deformation을 학습하는건데, face의 R|t를 직접 다 찾아내는게 아니라. R만 찾아내도록 하고 뒤에 Poisson solver를 붙여 최적화로 나머지 위치를 찾아낸다. 네트워크는 오로지 주어진 point feature와 global feature (optional)로부터 각 face가 어떻게 회전될지 그 gradient만 예측하도록 하면 된다. 자유도를 확 낮추고 뒤에서 최적화가 도는 방식이다보니까 효율적이고 성능도 높아 보인다.
수학이 묻어나는 논문이라 이것 역시 정확한 이해는 어려웠지만, 컨셉이 좋아서 기록해둔다.
메모
 |
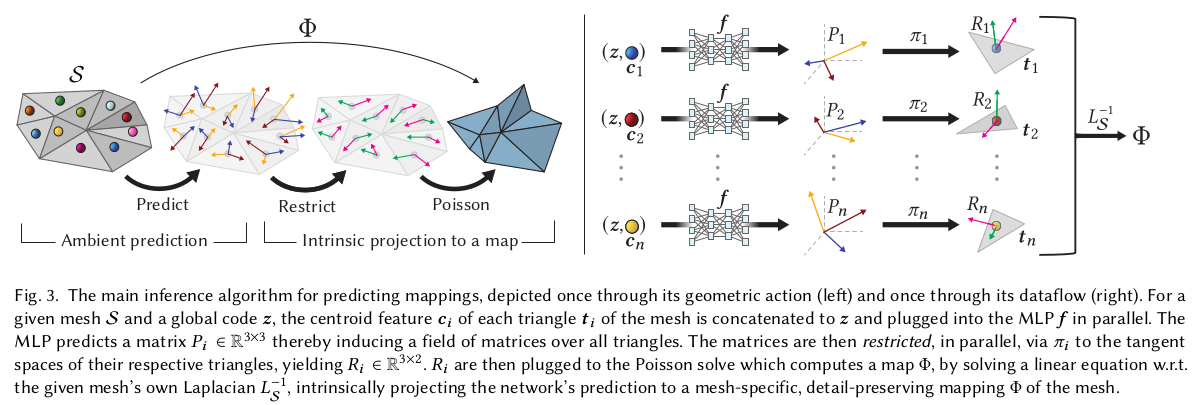
목적부터 딱 설명하고 시작한다. 임의의 mesh S가 주어졌을 때, 이를 대표하는 global code z 를 입력으로 원하는 대상으로 deformed mesh로 변형하는 알고리즘이다. 이 때 global code z는 target mesh를 표현하는 어떠한 latent vector도 가능하다. SMLP 파라미터든, point net으로 압축한 point든 CLIP 이든. |
  |
핵심으로 사용하는 수학은 다음과 같다. mesh face correspondecne A, B 가 주어져있을 때 둘 간의 관계는 수식(1)과 같이 jacobian과 A vertex, B vertex로 표현이 된다. 다르게 말하면 변형 후 vertex 위치를 모르더라도, 만일 jacobian만 계산해낼 수 있으면 B vertex를 역추정 가능하다는 소리다. -> 이 논문에서는 따라서 face 별로 MLP가 Jacobian을 계산해내도록 학습한다. -> 나머지는 수식(4)와 같이 알고 있는 값으로 최적화를 풀어 얻어낸다. |
 |
|
  |
 위 그림처럼 per-face feature가 global code와 함께 들어가면 face 별 3x2를 얻어내면 된다. 이 때 3x2를 바로 추정하기에는 어려우니 global coordiante 상에서 face 3x3 jacobian을 찾을 뒤, face로 projection해서 3x2를 만든다. coordinate 문제를 없애서 난이도를 낮춰주는 트릭. |
  간단히 말하면 MLP로 3x3 맞추게 하고 (여기서 point xyz, normal + wks라는 signal을 추가해준다.) -> 이건 좀 공부해야 알 수 있을 듯. wks 어려움 HKS에서 나온 것. |
 face의 orthonormal basis (평면을 구성하는) 로 projection한 뒤, poisson solver에 집어넣음 (differentiable solver) |
 |
 |
 |
 |
  |
학습은 MLP가 face 단위로 병렬처리하는 형태다 보니까 굳이 mesh 전체 face를 입력으로 할 필요없다. 배치 단위로 face 꾸러미를 묶어서 학습만 반복해주면 된다. global code를 보고 face 별 jacobian만 계산할 수 있도록 학습되면 됨. 나머지는 최적화로 풀거니까. |
  |
loss는 간단하다. 최적화가 완료된 결과와 GT 간의 vertex l2 distance 앞에 곱해진 lumped mass는 잘 모르겠다. 뭔지 아마 face 면적 비스무리한 가중치일 것 같다. + deformed mesh GT도 있으니, jacobian GT도 풀 수 있다. jacobian도 직접 l2 distance로 normalization 여긴 |tj| 가 face 면적 가중치인듯. -------------- xyz normal + wks를 같이 넣어주는게 성능 향상에 좋았나보다. 간단히 봤는데 wks는 vertex마다 energy 값인 것 같음. |
  |
여기서 하나 짚고 넣어가주는게 tangential plane으로 projection할 때 쓰는 orthonormal basis는 평면을 정의하는 basis니까 사실 무한개 있을 것(뱅글뱅글 돌면 되니까) 근데 이 basis는 어떤 걸 쓰던 별 차이 없다고 한다. 궁금하면 supplementary에 증명있다고 함.  |
 |
|
 |
 |
 |
|
 |
 컨셉이 좋아서인지 global code를 바꾸거나, mesh topology를 제한하는 등 활용하는 방법에 따라 다양하게 사용 가능한게 매력적인 듯. |
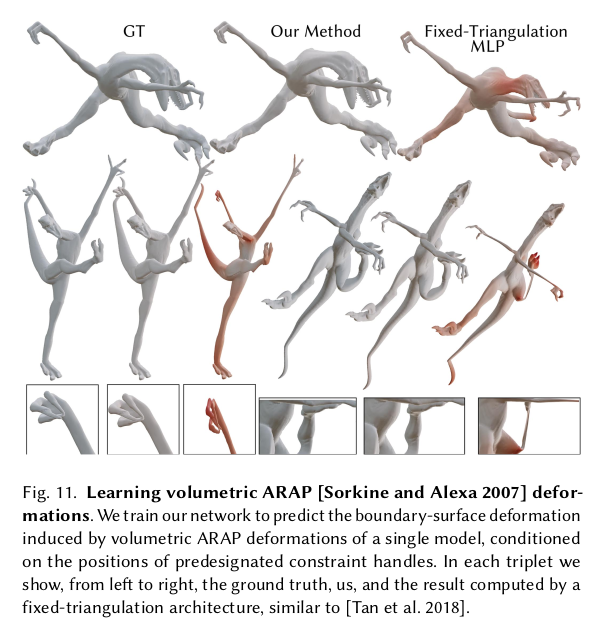 ARAP의 guidance로 사용하면 성능이 올라갈 정도. |
 |
 |
 |
  |
|
반응형