내 맘대로 Introduction

이 논문은 내 머리로는 한 방에 이해할 수가 도저히 없다. 수학, 수학, 수학한 논문이어서 수학 베이스가 약한 나로서는 이해할 방법이 없다. 이를 이해하기 위해서 파고들기엔 뭐를 봐야할 지도 잘 모르는 수준이어서 그냥 컨셉만 익히고 넘어간다.
이 논문의 핵심은 임의의 mesh가 주어졌을 때, vertex들을 어떻게 encoding해야 효과적으로 feature를 뽑아낼 수 있을지 그 방법을 설명하는 것이다. 예시가 사람이라서 human mesh 국한인 것으로 오해할 수 있으나, topology에 오류가 없는 mesh라면 어느 mesh든 적용 가능하다.
핵심 컨셉은 각 vertex를 동일한 가중치로 다루고 여기서 뽑은 feature도 동일하게 쓸 것이 아니라, 사전에 mesh topology 구성을 보고 어느 vertex feature가 얼마나 증폭되어야 하고, 얼마나 퍼져나가야 하는지를 계산해서 scale up해주는 느낌이다.
vertex feature를 단순히 scale up해주는 건 당연히 아니고, mesh topology에서 찾아낸 eigenvector들을 이용해 "diffusion"될 수 있도록 설계했다. 따라서 heuristic하게 face 면적이 작으니까 적게 퍼져나가고, 크니까 많이 퍼져나가는 그런 수준이 아니라 현 mesh 구조를 보았을 때 vertex가 해당 영역에서 실제로 영향을 펼치는 정도를 계산하는 섬세한 과정이다.
diffusion 만으론 동심원 퍼지듯 퍼져나가는 식으로의 확산 밖에 모델링하지 못하니, spatial gradient도 사전에 계산해서 non isotropic하게 퍼져나갈 수 있도록 추가 디자인한 것도 대단하다.
간략하게 설명하려고 해도 어려운 이 내용, 논문은 더 어렵다. 이해한다고 해서 활용을 더 잘할 수 있는 것도 아니니 가져다 쓴단 생각으로 가볍게 읽었다. (다른 사람들도 90%는 그랬으리라...)
메모
 위와 같이 서로 다른 topology 하에 학습된 네트워크는 성능이 오락가락한다. 모든 알고리즘에 topology depedency가 생기는데, 이는 vertex를 곧이 곧대로 독립적으로 쓰다보니, spaital resolution에 따라 네트워크가 편향되게 배우기 때문이다. 핵심은 spatial resolution, vertex density와 상관없이 mesh topology를 근본적으로 보고 배우게 하려면 어떻게 해야할까? |
 |
 |
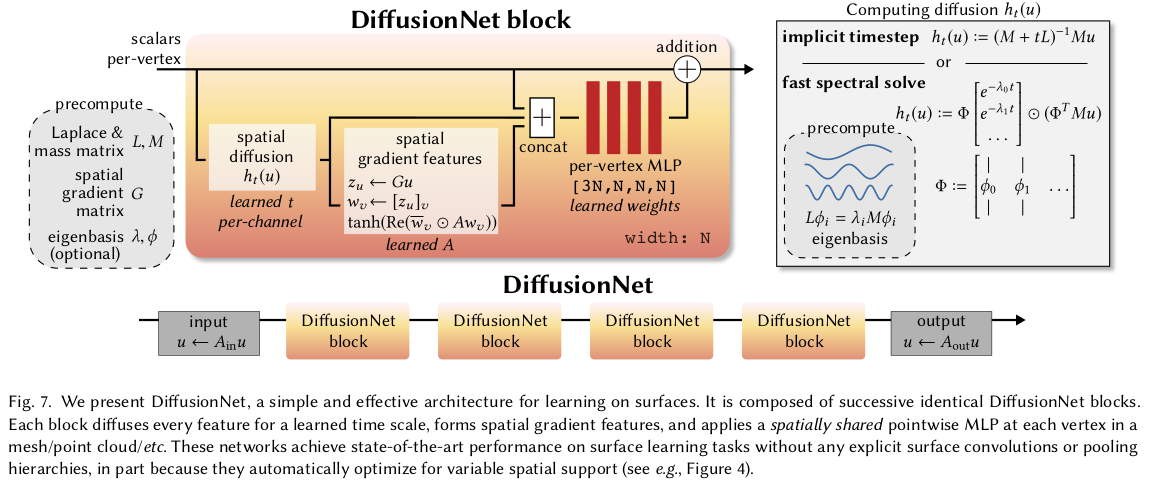
1) 일단 vertex feature를 뽑는건 해야함 D dimension 2) mesh topology에서 뽑아낸 정보로 vertex feature를 diffusion 시킨다. (일종의 isotropic scale up) 3) mesh topology를 보고 특정 방향으로 더 업데이트 (non- isotropic scale up 4) 이렇게 처리된 vertex feature로 뒤에 loss 계산 |
 |
1) vertex feature는 그냥 MLP 몇개로 추출 MLP가 vertex 간의 모든 연결을 다 체크할 뿐만 아니라 vertex 개별적으로 (batch) 처리하니까 컨셉에 맞음. |
  |
여기서부터 이해 못하기 시작. 내가 이해한 컨셉을 설명하면 다음과 같음 ----- 현 상태의 gradient를 알면 time step을 곱하면 다음 값을 approximation으로 알아낼 수 있다. (linear 하다고 보니까) 그 gradient를 구하는 방법을 heat equation에서 착안해오면, 어떤 값에 laplace beltrami operator를 곱하면 되는 모양이다. (surface 상에서 gradient를 계산하는 연산자이자 matrix라고 보면 됨) 여기서 Laplace beltrami operator는 또, mesh surface 상에서는 한 번 더 분해(approximation)이 가능한데 그건 mesh surface로부터 뽑아낸 2개의 matrix로 표현할 수 있다는 것. 따라서 알고리즘이 다룰 방법은 1) 사전에 mesh에서 L, M matrix 뽑아내둠 2) laplace beltrami operator 계산 해둠. (이것도 뒤에서 약간 변형함) 3) vertex feature를 diffusion 시켜서 사용 ------------------- 이렇게 하면 마치 convolution 하듯이 mesh vertex가 neighbor로 영향력을 펼쳐나가기 때문에 굳이 따로 convolution 컨셉을 넣지 않아도 locality 확보가 가능하다고 함.  시각화 해봐도 잘 퍼져 나감. 저 t는 learnable |
  |
하나도 이해 못해버리기. 여튼 이렇게 하면 최소 1ring neighbor, 2ring neighbor와 같이 퍼져나가듯이 feature 확산 가능. |
 |
아까 L, M matrix를 갖고 laplcae beltrami operator를 계산할 수 있다고 말했는데 approximated form으로 구할 수 있다. 간단히 적었지만 저 ~~를 구체적으로 위의 식보다 더 정확하게 approximation하는 방법이 있을 것. 총 2가지를 제안한다. 그중 첫번째는 그냥 linear하게 모델링하는 것 수식(2)가 그렇다. 이 방법이 실험적으로 괜찮았지만, 하나 단점은 vertex 수가 많은 경우에 조금 불리한가봄. --- L, M을 어떻게 만드는지는 아래 수식(3) + solver 임 |
  |
두 번째 approximation 방법은 mesh surface에서 뽑아낼 eigenvector를 갖고 더 섬세하게 디자인하는 방법임. linear 대신 eigenvector와 eigenvalue를 같이 연산하는 방식으로 L, M matrix의 영향력을 vertex 별로 다르게 들어갈 수 있도록 한 방식. eigenvector가 엄청 많을 거니  그중 표현력이 충분한 128개 정도로 선별해서 low frequency basis만 사용함 -------------- high frequency도 버리냐? 라고 할 수 있는데 뒤에 따라붙는 기타 모듈들이 vertex feature를 보고 알아서 해줄 거라 믿는 것. |
 |
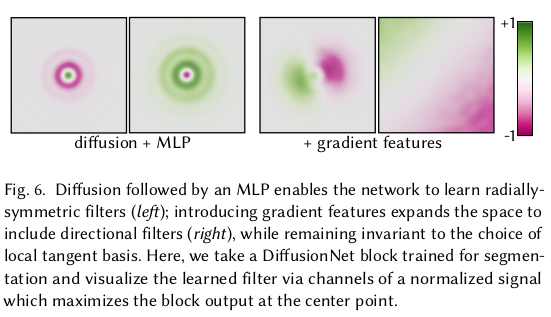 위 방식대로 diffusion만 모델링해도 되지만, isotropic diffusion 밖에 표현이 안된다. 위 그림처럼 vertex가 있으면 균일하게 퍼져나가는 식의 확산만 된다는 편. 근데 실제 mesh surface는 굴곡이 다양한 편이므로, 그 굴곡까지 반영해서 diffusion 될 수 있게 해주면 더 효과가 좋지 않을까? 라는 생각에서 spatial gradient feature 모듈을 추가한다. |
 |
요약하자면, 1) vertex가 속해있는 face의 normal정보를 이용해서 해당 vertex에 gradient를 계산한다. 2) gradient 를 learnable matrix A와 함께 짬뽕해서 새로운 feature g를 만듦 3) 기존 vertex feature에 합치기.  이해는 못했지만, 이렇게 non-isotropic 요소를 추가해줌으로써 대칭적 요소에 대한 구분력이 더 상승됨. 굴곡까지 반영한 vertex feature 확산이 가능해지니까, 구분력이 상승된 것. 그걸 실험하기 위해 대칭 판별 toy example을 보여준 것. |
 |
|
 |
컨셉과 사전 계산해둬야 할 mesh property가 많아서 그렇지 네트워크 구조는 간단함 MLP + spatia gradient feature 추출 + 다시 MLP + diffusion 임 이걸 하나의 block을 생각해서 N 번 반복하면 mesh topology를 반영한 vertex feature 완성!  맨처음 입력으로 x,y,z를 넣을 수도 있고 더 구분력을 높이기 위해서 HKS를 넣을 수도 있다고 함. (뭔지 모름. 근데 그냥 모르면 xyz 넣어도 되겠더라.) |
 |
 |
 이 방법을 이용해서 다른 vision task 문제를 풀어보면 성능이 좋음. 대표적으로 3D Segmentation을 주로 보여줌. |
 |
 |
|
  |
 |
 |
사전 계산해두는 term이 많은 관계로, 사전 계산값들이 틀어지는 mesh, 즉 끊겨있거나 hole이 뚫려있는 mesh에 취약하다. |
