반응형
내 맘대로 Introduction
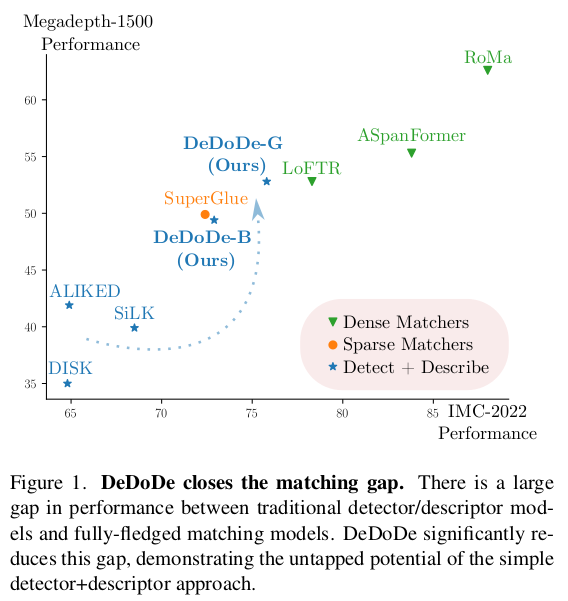

이 논문은 DKM, RoMA 저자가 쓴 후속 논문인데, dense matching을 떠나 sparse matching으로 다시 돌아와 쓴 논문이다. 하지만 dense matching의 결과를 가져와서 학습에 supversion으로 사용할 수 있도록 설계했기 때문에 사실 상 dense matching distilled sparse matching으로 만들 수도 있다. superglue를 이기기 웬만해선 힘들 것이라고 생각했는데 간단함에도 단숨에 뛰어넘는 것을 보고 진짜 이 연구자는 실력이 미쳤구나 싶었다.
핵심 아이디어는 descriptor와 detector를 완전히 분리해서 학습시키는 것이다 어찌보면 PoSFeat과 결을 나란히 하는 논문이다. (posfeat 이슈에 보면 이 사람이 남긴 이슈가 있어서 이런 연구할 것 같았는데 바로 나와서 경악했다...) detector를 먼저 description 개념하나 없이 따로 학습하고 descriptor는 freezed detector 갖고 별도로 학습하는 식이다.
네트워크 구조도 VGG19 + DKM decoder (왠지 RoMa에서 발견한 VGG19의 locality 특성이 여기서도 도움이 됐나 싶다.) 로 간단하고 DKM을 follow up 했다면 쉽게 접근할 수 있다. CNN backbone이기 때문에 backbone 교체나, 해상도 조절, 경량화 작업 등 열린 부분이 많아 여러모로 가치있는 연구라고 생각한다.
메모하며 읽기
 |
|
  |
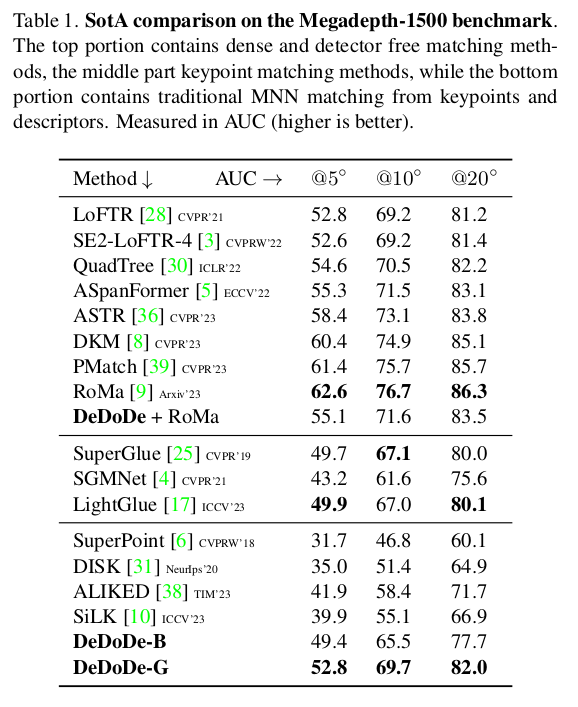
왜 decoupling을 한 detector+descriptor를 만들고자 했는지 설명하는 단락인데, 전통적으로 해왔던 방식을 버린 이유는 세가지다. (의미로만 보면 2가지) 첫번째로 descriptor에 구애받지 않는 형태이면 나중에 더 좋은 keypoint detector가 등장했을 때 이를 활용할 수 있기 때문이다. (이 논문이 self-supervised라서 그런듯. ) 두번째로 성능이 결과적으로 뛰기 때문이다. keypoint는 잘 뽑히지만 descriptor 때문에 matching이 실패하는 경우 (edge, corner)나 deep descriptor는 잘 뽑히지만 keypoint는 잘 안 뽑히는 경우(textureless plane)을 보면 각각 잘하는 걸 잘하도록 분리하고 연결해주는 것이 좋은 접근일 수 있다는 생각을 했다. |
  |
먼저 detector다. detector의 object는 수식(3) 과 같다. 결국 주어진 이미지에서 keypoint가 될만한 위치에서 확률값이 높게 나오고, 그 외에는 (- 이후 term) 0에 가까울수록 좋다. 문제는 그럴만한 GT가 없다는 것이다. 사람이 안 만들어서 없는 것이 아니라 절대적으로 True keypoint가 뭔지 정의할 수가 없기 때문에 못 만드는 것이다. 그나마 GT에 근접하다고 의미를 둘 수 있는 keypoint는 3D reconsturction에 triangulation해서 사용했을 때 실제 형상에 맺히는 점 정도라고 정의할 수 있겠다. |
 |
그렇게 정의해서, 저자들은 SfM 데이터셋에서 3D-2D correspondence+covisibility를 GT로 이용했다. SfM 결과로 잘 3d point로 triangulation 된 2d point들만 keypoint GT라고 정의했다. |
 |
|
  |
학습을 어떻게 시키느냐! 일단 GT keypoint로 distribution을 만든다. gt.kp 위치를 dirac delta function(정확히 gt.kp 위치만 값을 1로 채움)을 통과시키고 std 0.5 인 gaussian kernel로 주변을 채웠다. constant C는 uniform distribution에서 뽑은 상수라고만 적혀있어서 뭔지 잘 모르겠으나 아마 gt.kp 위치에 따른 가중치같은게 아닐까?(코드를 봐야알듯, 혹은 중요하지 않아서 설명 생략한걸지도) 위와 같이 image A, B에 대해 각각 모든 kp를 distribution화 해서 채웠으면 이를 GT depth + GT camera pose를 이용해 A<->B가 pixel by pixel로 align 되도록 한다. 그리고 서로 곱한다. 이러면 양쪽 이미지에서 keypoint-ness + depth + camera pose가 모두 맞아떨어지는 아이들만 높은 값을 갖도록 살아남는 keypoint heatmap이 된다. ---- 이 keypoint heatmap은 GT로부터 만든 것이기 때문에 detector가 참고하기 매우 좋은 값이므로 prior라고 불린다. 여기서는 megadepth GT를 썼지만 warping관계만 정의할 수 있다면 (특히 RoMA나 DKM!!) GT를 생성할 때 다른 dense matching 알고리즘을 쓸 수 있다!! 이게 핵심인듯. |
   |
실제 학습은 위 prior를 p^kp라고 하면 수식(8)과 같이 detector가 내뱉는 확률 분포랑 p^kp를 곱해서 만든 p를 사용해서 진행한다. 이렇게 하면 p^kp가 높은 곳은 그대로 높도록 유지하면서, 가령 p^kp가 낮더라도 keypoint일 확률이 높은 대는 p_ftheta가 높아져서 보상할 수 있으므로 prior 이상의 효율을 내기 쉽다. (아래에서도 지적하지만, 0~1로 표현된 값이기 때문에 p^kp가 0에 가까워 버리면 사실 p_ftheta가 아무리 높아져 봤자 1에 근접할 수 없다. 그래서 "optimal"하진 않다고 하는데 실제로 해보면 네트워크 빨로 어찌저찌 잘 되긴 한다고 한다.) p를 그렇게 prior를 깔고 가는 형태로 정의하고 p (network + prior) == p_ftheta(network)와 같아지도록 강제한다. 이게 좀 애매해보이는데, 이렇게 하면 어쨌든 optimal하진 않지만 prior를 깔고 network output이 prior보다 잘될 수 밖에 없긴 하다. 애매한 부분은 수식 (10)과 같이 MVS 3d point를 갖고 만든 진짜 찐GT로 한번 더 걸어줌으로써 보상한다. |
 |
확률 분포를 keypoint화 하는 방법은 단순히 softmax 후 non-maximal suppression하는게 아니라 SiLK에서 쓰는 방법을 썼다고 한다. (probability 갖고 하는 방법이 있나봄) 구조는 VGG19 + DKM decoder다. 둘 다 RoMa에서 locality를 인정받고 decoding 성능을 인정받은 구조다. |
  |
descriptor 는 이제 detector 수렴이 끝난 후 freeze하고 사용한다. descriptor가 달성해야하는 목표는 주어진 B feature 중 가장 잘 맞는 A feature를 찾는 것 + 주어진 A feature 중 가장 잘 맞는 B feature를 찾는 것이다. 이게 수식 (13)의 의미인데, keypoint AB pair 하나 마다 이걸 계산해서 높일 수 있도록 loss를 설계했다. correspodence끼리만 이걸 계산하면 당연히 모두 단 하나의 descriptor로 수렴하면서 평균에 수렴하려고 할 것이다. 따라서 이를 막기 위해 모든 keypoint 간의 서로서로 다 매칭하면서 비교했다. 이렇게 되면 모두가 높아져버리면 수식(12)의 분모가 커져 확률이 낮아지므로 경쟁적으로 최적의 매치를 찾게 된다. |
 |
descriptor network구조는 조금 더 얇을 뿐 detector network랑 동일하다. (모델을 꽤나 무겁겠다. 일단 2배니까) 추가로 RoMa에서 썼듯이 DiNOv2 feature를 가져와서 넣어주는 식으로 학습을 보조했을 때 성능이 좋아지기도 해서 선택적으로 쓴다고 한다. |
  |
|
 |
 |
  |
 |
 |
반응형
'Paper > 3D vision' 카테고리의 다른 글
| 4D Gaussian Splatting for Real-Time Dynamic Scene Rendering (0) | 2023.11.03 |
|---|---|
| Detector-Free Structure from Motion (0) | 2023.11.02 |
| 3D Gaussian Splatting for Real-Time Radiance Field Rendering (0) | 2023.11.02 |
| NeRF−−: Neural Radiance Fields Without Known Camera Parameters (0) | 2023.10.30 |
| BARF : Bundle-Adjusting Neural Radiance Fields (0) | 2023.10.30 |