반응형
내 맘대로 Introduction

이 논문은 제목에서도 알 수 있다시피 Mip-NeRF의 확장판이다. 사실상 Mip-NeRF++과 같은 개념이다. 타겟으로 하는 문제는 Mip-NeRF의 방식을 그대로 사용하되, 특정 크기로 한정하기 애매한 공간을 복원하는 방법이다. 무슨 말이냐면, 기존 방식들은 예를 들어 지름 1m 구체 안에 물체가 있는 경우와 같이 특정 공간을 한정하고 복원을 했다. 하지만 위 그림과 같이 한 물체를 중심에 두고 뱅글뱅글 돌면서 찍을 경우 배경은 지름 1m 구체를 한참 벗어난 영역에서 온 색상이기 때문에 쉽게 모델링할 수 없다.
결과적으로 지름 1m 구체 안에서 하늘 색깔도 표현해야 하고 멀리있는 나무 색깔도 표현해야 하니, 물리적으로 안맞는 상황 때문에 성능 저하가 있다는 문제를 풀고자 했다.
핵심 아이디어는 물리적 크기로 공간을 잡는 것이 아니라, 무한대의 공간이 특정 크기로 압축되도록 하는 것이다. 다른 말로 무한대의 공간이 지름 2m구체 안에 갇히도록 압축하는 함수를 개발해서 Mip-NeRF에 추가한 셈이 되겠다.
메모하며 읽기
 |
Mip-NeRF360에서 크게 다루는 contribution 중 하나는 앞서 언급한 무한대의 공간을 2m 지름 구체 공간 안으로 압축하는 방법론이다. 가까우면 자세히, 멀면 대충 봐도 되는 상황과 맞아떨어지기도 하는 내용이다. |
  |
공간을 압축하지 않고 모델 사이즈를 키우거나 하는 방식으로 하면 모델 사이즈가 복원 대상 공간 크기에 폭발적으로 비례하기 때문에 문제가 많다. 따라서 공간 압축하는 것이 효과적이고, 더불어서 NeRF가 coarse sampling, fine sampling 두 단계로 ray sampling을 하는데 이 중 coarse sampling은 실질적으로 중요하게 안 쓰이는데 loss 계산이다 뭐다 계속 사용되므로 연산량이 늘어난다고 한다. 따라서 구조도 proposal MLP, NeRF MLP로 나눠서 효율을 늘렸다고 한다. |
  |
Mip-NeRF recap~ cone frustrum으로 확장한 내용과 그에 대응되는 integrated positional encoding을 설명해주는 내용. |
  |
IPE(Integrated positional encoding)을 쓸 것인데 지금 대상 공간이 이전과 달리 함수 f()에 의해 압축된 공간이기 때문에 약간의 수식 변화가 필요하다. 압축 함수 f가 실제로는 non-linear하겠지만 일단 linear하다고 approximation하고 출발하면 주어진 공간 정보 mean, std를 갖고 수식 (8)과 같이 표현할 수 있다. (주어진 공간이 너무 넓을 경우 혹은 카메라에서 너무 멀 경우에는 안 맞겠지만 그런 상황은 흔치 않으니 나름 합리적인 가정일지도) linearize가 일단 되면 함수 f에 대한 mean, std를 계산하는 것도 쉬워진다. 결과적으로 압축된 공간에 적용할 수 있는 IPE가 정의된다. 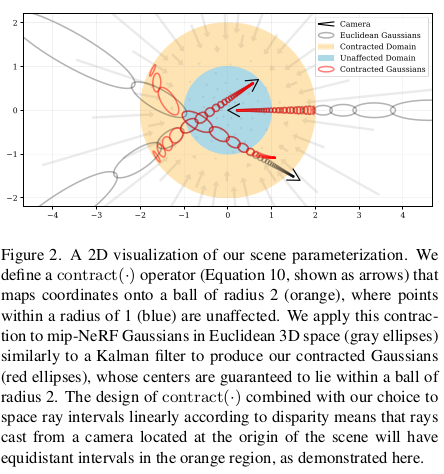 실제로 f 버전 IPE를 보면 위와 같이 압축된 공간 상의 공간을 나름 잘 표현하고 있는 것을 볼 수 있다. (카메라 위치가 구의 중심에서 멀어질 경우 약간의 왜곡이 있는 것 같은데 이건 앞서 내가 예상한대로 인 것 같고 그냥 무시하는 것 같다.) |
  |
개념적으로는 위와 같이 정의하면 끝인데 실제로 구현할 때는 ray sampling을 해야된다. 이 때 압축된 공간에서 uniform sampling할건지, 압축 전 공간에서 uniform sampling할 건지에 따라 성능이 달라질 것이라는 것은 직관적으로 알 수 있다. 대충 말하면 압축 후 공간에서 linear하게 뽑는 것을 지향한다. 이를 구현하기 위해서 실제 물리적인 거리 t로 near-far를 표현하는 것이 아니라 mapping g를 이용해 새로 정의된 거리 s 0-1로 표현했다. 그리고 s 상에서 linear하게 sampling했다. g는 여기서 1/x 즉 역수로 쓰였는데 이렇게 하면 대충 가까울 때는 많이 뽑히고, 멀 때는 듬성 듬성 뽑히게 된다. (이해가 안되면 1/x 그래프 그려놓고 y값을 등간격으로 쪼갠 후 대응 되는 x 위치들을 찍어보아라.) 이 모양이 완벽하게 contract(x)함수와 맞아떨어지는 모양은 아니지만 경향을 같이 하므로 그냥 이렇게 쓴 것 같다. 어차피 sampling일 뿐이고 weight를 보고 fine sampling할 것이기 떄문이다. |
  |
또 다른 이슈로 언급한 것은 NeRF 구조 중 coarse MLP의 비효율성이다. coarse MLP에서 나온 color를 supervision에 쓰긴 하지만 어디까지나 coarse MLP의 역할은 fine MLP가 보다 좋은 영역에서 sampling을 할 수 있도록 가이드 해주는 역할이다. uniform sampling으로 의미없는 영역에서 sampling하고 color를 뽑는 coarse MLP는 오히려 supervision을 걸어주면 방해가 될 수도 있다는 말이다.  따라서 이 역할에 충실해서 저자들은 coarse MLP 대신 fine MLP의 sampling을 도와주는 역할만 담당하는 proposal MLP를 추가했다. Proposal MLP는 color supervision 걸리는 것 없이 오로지 fine MLP의 sampling 후보군을 추려주는 역할만 한다. 이렇게 설계하고 학습을 해보면 fine MLP가 학습이 되어감에 따라 fine MLP가 proposal MLP에게 더 정확해지라고 강제하는 모양이 되므로 online distillation이라고 부른다. proposal MLP는 역할이 줄어들었으므로 얇게, fine MLP는 비교적 크게 사용한다. |
 |
color supervision을 안 쓰면 proposal MLP를 어떻게 학습시키냐. 그 방법을 생각해보면 일단 딱 하나, fine MLP가 뽑은 영역과 비슷해야 한다는 점이다. 여기서 착안해서 fine MLP에서 뽑은 영역과 겹치면 loss 없음, 안 겹치면 loss 있음 형태로 구현하면 된다. 또 proposal MLP에서 나온 sampling weight이 fine MLP에서 나온 sampling weight 보다 크면 안된다. 뭔소리냐면, 후보군을 추려주는 역할만 해야지 뒤에 최종 위치 뽑는 녀석보다 처음부터 확신있게 말하면 안된다는 소리다. 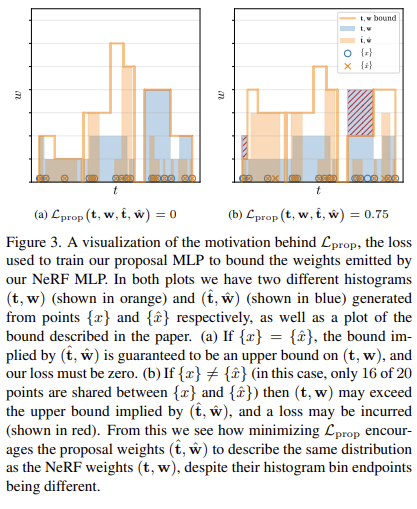 이를 구현하는 방식은 fine MLP 에서 나온 weight로 bound를 그려서 그 내부에 무조건 위치하도록 하는 것이다. 벗어난 영역만큼 패널티를 가한다. |
 |
이렇게 설계하면 무조건 fine MLP에 의해서 proposal MLP가 그 범위를 넘지 않도록 예측하기 때문에 일방적으로 teaching하는 구도가 나온다. (online distillation, 이 파트에서는 assymmetric하다고 표현했다.) proposal MLP 결과는 순전히 proposal후보군 추리는 것에서만 영향을 받을 수 있도록 gradient를 끊어주는 것도 했다고 한다. 그림 3 보면 이해가 빠르다. 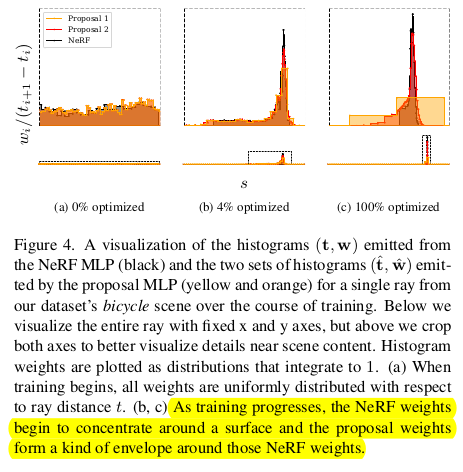 학습을 실제로 해보면 의도한대로, fine MLP 값에 갇힌 형태로 proposal이 잘 나와주는 것을 볼 수 있다. |
  |
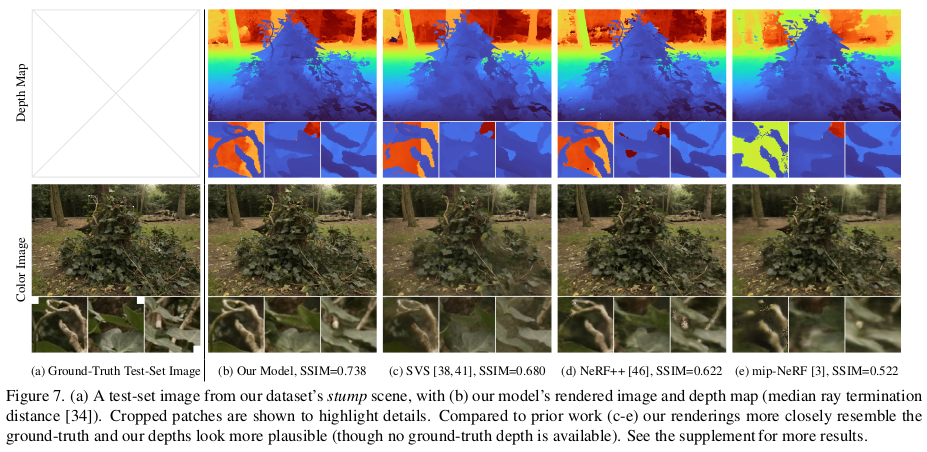
학습할 때 압축된 공간에서 sampling을 해서 인지 구름 같이 떠있는 노이즈나 배경 뭉개지는 현상이 있었는데 이를 해결하기 위해 regularization도 추가했다. 일반 NeRF에서 쓰는 방식을 써서 weight 자체를 억누르는 식으로 해도 되지만 굳이 새로 디자인했다. 이게 더 좋나보다. 수식(14)인데 대충 의미를 보면, 위치 2개를 딱 뽑았을 때 서로 가까우면 weight가 커도 문제 없음, 근데 서로 멀면? weight가 둘다 크면 안된다. 이를 해석해보면 ray 마다 웬만하면 surface가 하나일테니 한 위치 근방에서만 weight가 높게 나와야 한다. 가까운 두 점을 뽑았을 때 만약 surface 근처였다면 둘다 weight가 높게 나올 가능성은 있지만 먼 두 점을 뽑았을 때는 둘 다 surface에 가까울 리가 웬만하면 없으므로 weight가 낮게 나와야 된다는 논리다. 실제로 surface가 여러개 겹치는 ray면 의미가 줄어들겠다만 웬만하면 surface 한 번 만날테니까 의미가 있다. 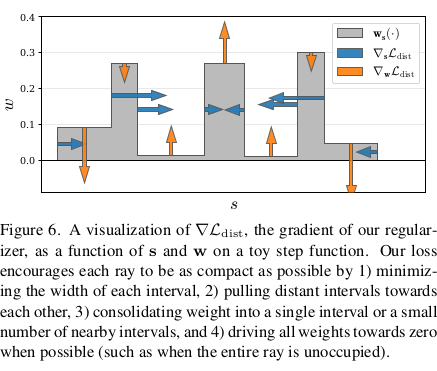 그림으로 보면 이해가 쉽다. 이 loss로 억제를 하면 위 그림과 같이 여러개 peak가 나올 수 없도록 만들어 준다. surface가 웬만하면 1개만 걸리도록 강제하므로써 공중에 떠있는 구름 노이즈나 배경 뭉개지는 것이 억제되는 것이다. 구름 노이즈가 있으면 여기 저기서 weight가 높을테니 말이다. |
  |
구현 디테일인데 특별한 것은 없고, color loss를 MSE loss 안 쓰고 Charbonnier loss 썼다고 한다. 사실 상 sqrt 안에 epsilon 더해준 간단한 형태. 이게 더 수렴을 잘했다고 한다. |
 |
|
 |
 |
반응형
'Paper > 3D vision' 카테고리의 다른 글
| Self-Calibrating Neural Radiance Fields (0) | 2023.10.30 |
|---|---|
| Level-SfM: Structure from Motion on Neural Level Set of Implicit Surfaces (0) | 2023.10.30 |
| Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields (0) | 2023.10.24 |
| Progressively Optimized Local Radiance Fields for Robust View Synthesis (0) | 2023.10.23 |
| Neural Kernel Surface Reconstruction (0) | 2023.10.20 |
