내 맘대로 Introduction
이 논문은 NeRF에서 pixel마다 ray를 1개 할당하는 방식을 다르게 바라본 논문이다. 실제로 pixel 1칸에는 광선 1개가 담겨 색깔을 결정하지 않는다. pixel이 점이 아니고 실제론 면이기 때문에 frustrum에 속하는 광선 무한개가 모여 색깔을 결정한다. 이러한 물리적 특성을 그대로 반영하려면 NeRF를 구현할 때도 pixel 당 ray 개를 할당할 것이 아니라 pixel 당 frustrum을 할당하는 것이 맞다는 논리다. 실제로 이렇게 모델링이 되면 공간에 들어차있는 color나 opacity가 더 자연 현상과 가깝게 될 것이다.
논문의 핵심은 ray 대신 frustrum을 쓰는 것 + frustrum에 걸맞는 positional encoding을 새로 디자인한 것이다. 사실 후자가 핵심이고 나머지는 같다. 후자를 디자인할 때 기존의 ray 1개를 위한 positional encoding의 특성 및 장점들을 잃지 않도록 유지하는 것 + 구현을 간단하게 만들 수 있는 것에 힘썼다. 수학적으로 전개한 것이 강점인 논문이다.
이름 자체는 graphics 쪽에서 texturing을 다룰 때 사용하는 mip-map technique에서 따왔다. 이게 뭐냐면,

매번 해상도에 맞춘 texture를 실시간 계산하면 연산량이 너무 커지기 때문에 특정 해상도로 미리 texture들을 생성해두고 실시간으로는 이 값들은 interpolation하는 방식으로 대충 approximation하는 방법이다.
Mip-NeRF에서 frustrum을 계산하는 방법도 실시간으로 하자면 연속적인 모든 위치를 다 커버해야 하므로 연산량이 매우 커지는데 mip-map과 같이 특정 위치들을 기반으로 approximation하는 식으로 단순화했기 때문에 비슷한 컨셉이라 이름을 따왔다.
메모하며 읽기
 |
 Mip-NeRF는 ray를 frustrum 단위로(여기선 cone으로 정의했다.) 사용하기 때문에 위 그림과 같이 일반 NeRF였다면 특정 위치가 점으로만 다루어졌겠지만, 면적(부피)으로 네트워크에게 다루어진다. 따라서 네트워크 입장에서 어떤 위치, 점만 보는 것이 아니라 지금 해당 위치가 주어진 이미지들로 미루어보았을 때 얼만큼의 부피를 차지하는 위치인지 까지 같이 배우게 된다. 이러한 컨셉으로 인해 기존 NeRF는 coarse, fine 2 stage로 풀던 성능 문제를 단 하나의 stage로 풀 수 있게 되는 강점도 있다고 한다. 그로 인한 속도 향상이나 모델 사이즈 감소도 큰 이득이 있다. |
  |
frustrum은 여기서 cone으로 다뤘다. 사실 사다리꼴보다는 원뿔이 표현하는 파라미터가 작기 때문에 다루기 쉬울 뿐더러 뒤에 approximation을 적용하기 더 쉬운 형태여서 그런 것 같다. ray 1개를 다룰 때는 x, o, d 3개만 필요했다면 이제는 pixel에서 시잘할 때 반지름 r, frustrum 범위 시작-끝 t0, t1) 3개가 더 필요하다. 특정 위치가 frustrum에 해당하는지 아닌지, indicator function, F를 정의해서 학습에 사용하는데 indicator function은 원뿔을 가정하면 수식 (5)와 같이 간단히 계산할 수 있다. 이때 반지름 r은 픽셀 너비의 2/sqrt(12)로 했는데 이게 왜 그러냐면 실제로 pixel은 사각형이라서 사다리꼴 frustrum인데 원뿔 frustrum으로 퉁치는 과정에서 발생하는 차이 때문이다. 원뿔이 사다리꼴 frustrum 안에 내접하면서 꽉 차도록 하려면 2/sqrt(12)로 나누어준 값으로 시작해야 한다. |
  |
frustrum으로 다루면서 입력 x가 점이 아닌 부피가 되었는데, 결국 입력으로 넣어줄 때 positional encoding으로 변환해서 해주므로, 부피용 positional encoding이 필요하다. 가장 단순한 방식은 수식(6)과 같이 부피 내의 positional encoding 값을 적분 해서 사용하는 방식인데 이렇게 하면 기존 positional encoding의 특징 및 장점을 못 살린다. 각 위치가 unique한 것 + frequency가 주는 특징을 살릴 수 없음 따라서 이를 살리기 위해 multivariate Gaussian으로 modeling하는 방식을 정의했다. 원뿔형 frustrum이기 때문에 ray 방향과 반지름 방향의 std, ray 방향의 거리 mean만 있으면 된다. 이렇게 정의하면 특정 cone frustrum을 정의하는 세가지 변수는 수식(7)과 같이 쉽게 계산할 수 있다. 이 세가지 변수를 이용하면 cone 전체의 위치 정보를 대략적으로 나타낼 수 있다. |
  |
위와 같이 multivariate Gaussian으로 정의한 이유는 간단함 뿐만이 아니다. 일반 positional encoding을 matrix form으로 다시 표현해보면 수식 (9)와 같이 되는데 x가 더 이상 점이 아닌 분포가 되었을 때 linear transform 특성에 의해 positional encoding도 분포 버전으로 손쉽게 바꿀 수 있다. x의 mean,std를 알면 Px의 mean,std를 간단히 계산할 수 있기 때문이다. Px도 분포 버전으로 구할 수 있게 되면 positional encoding의 분포 버전도 대입만 하면 되니 수식(11) (12)와 같이 얻을 수 있다. 여기서 covariance를 구하는 연산이 큰 matrix multiplication이므로 연산량이 많을 수 있는데 대각성분을 제외하면 0이 들어차있는 특수한 matrix이므로 수식(15)와 같이 decompostion해서 풀면 연산량을 크게 줄일 수 있으므로 큰 문제가 되지 않는다. 결론적으로 일반 positional encoding과 큰 연산량 차이 없이 분포 버전(부피 버전) positional encoding을 계산할 수 있다. |
 |
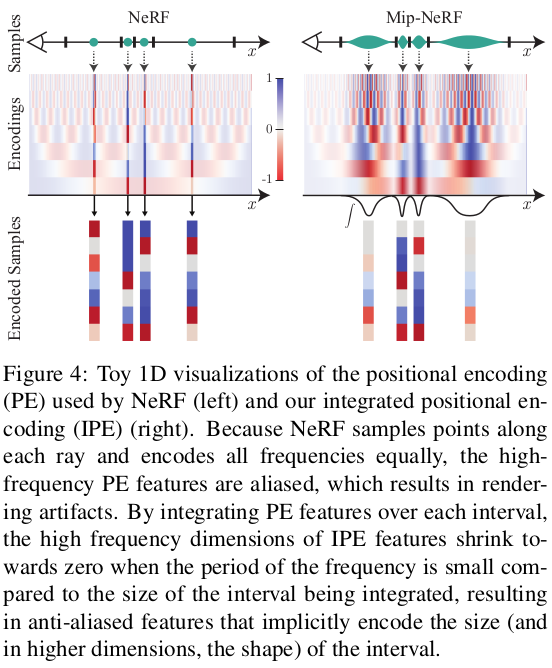 이렇게 학습한 분포 버전 positional encoding을 시각화해보면, 실제로 한 위치만 표현하는 일반 PE 대비 공간 내 여러 영역에 대한 표현력을 갖고 있음을 알 수 있다. frustrum 부피를 넘어서는 frequency 영역의 encoding 값은 자연스럽게 0에 가까워지므로 frustrum 부피에 대한 민감도를 충분히 갖추고 있다. coarse, fine 구분력이 positional encoding에 내장되었다고 할 수 있다. |
   |
구현적으로 수식을 NeRF와 동일하다. coarse sampling하고 나서 fine sampling하는 것도 동일하다 다만 coarse MLP, fine MLP를 구분하지 않고 같은 MLP에 두 가지 sampling을 다 넣어줄 뿐이다. 그 이유는 앞서 설명한 것과 같이 IPE가 coarse, fine 구분력을 내장한 positional encoding이므로 알아서 학습할 것이기 때문이다. 굳이 coarse, fine sampling을 그대로 냅두는 이유는 이 방식이 sampling만 보았을 때 좋은 방법이기 때문이다. 대충 뽑고 대충 뽑은 위치 weight 보고 그 주변에서 또 뽑는 방식은 충분히 좋은 방식이기 때문이다. 다만 뽑은 위치가 이제 점이 아니라 frustrum이므로 수식(18)과 같이 뽑은 범위의 weight를 평균내는 방식이 새로 조금 필요했을 뿐이다. |
 |
|
 |
 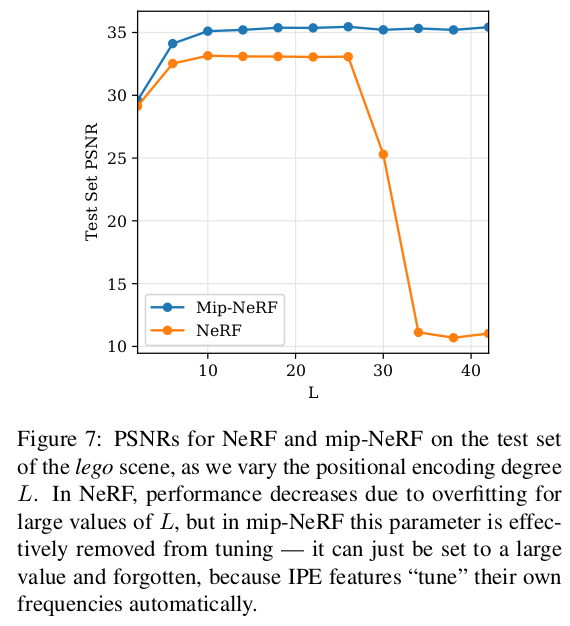 |
 |
'Paper > 3D vision' 카테고리의 다른 글
| Level-SfM: Structure from Motion on Neural Level Set of Implicit Surfaces (0) | 2023.10.30 |
|---|---|
| Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields (0) | 2023.10.25 |
| Progressively Optimized Local Radiance Fields for Robust View Synthesis (0) | 2023.10.23 |
| Neural Kernel Surface Reconstruction (0) | 2023.10.20 |
| Neural Fields as Learnable Kernels for 3D Reconstruction (0) | 2023.10.19 |