반응형
내 맘대로 Introduction

Gaussian-to-Mesh에 속하는 논문인데, 3DGS에는 3DGS->2DGS로 내려찍는 방식으로 하는데 반대로 조금은 느리겠지만 NeRF에서 원래 하던 방식대로 pixel-to-ray를 만들고 ray tracing하면서 3DGS를 적분해나가는 식으로 바꾼 논문. 왜 이 불편함을 감수하느냐. ray 단위로 다시 시선을 바꾼 다음 적분하기 시작하면 NeRF에서 그랬듯 surface를 찾기 쉬워지기 때문이다.
이 논문에서는 3DGS를 학습할 때 surface를 쉽게 찾아 meshing 난이도를 낮추기 위한 loss로 제안하지만 그보다 더 핵심은 어떻게 주어진 3DGS에 NeRF에서 쓰던 ray 단위의 적분을 적용할 것이냐다.
메모
  |
세팅은 일반 3DGS랑 완벽히 동일함. 추가 primitive가 있는 것도 아님. 그래서 꼭 이 논문에서 제안하는 방식으로 학습한 개체가 아니더라도 mesh로 그대로 바꿀 수 있음 |
 |
 핵심은 pixel 단위로 ray를 쏘고 그 과정에서 부딪히는 모든 3DGS를 거리 순서대로 NeRF처럼 적분해서 surface를 찾아내는 것. 3DGS가 2D projection을 통해 가속했던 부분이 사라지므로 속도는 좀 느려짐. 뒤에 나오는데 ray를 따라가다 3DGS에 진입하면 해당 3DGS에서 opacity 값을 뽑아내서 쓰면 되고 (거리 기반으로), 하나 차이점은 3DGS 센터를 넘어갔다면 그때부터는 최대opacity를 계속 뽑아내서 쓴다. 이건 직관적으로 ray가 앞쪽에서 오기 때문에 3DGS를 통과 이후엔 계속 가려짐 효과가 생긴다. 이걸 반영하기 위해서 통과 이후엔 실제 opacity 값이 어떻든 다 최대값으로 한다. 3DGS의 중심은 찾기 쉬우니 계산도 간단. |
 |
렌더링을 해서 색상을 얻어내야 할때는 ray 컨셉을 굳이 고수할 이유가 없다. ray 단위로 구현할 부분은 surface를 찾아낼 때 뿐. 따라서 색상을 만들땐 원래 3DGS 방식 그대로 사용한다. projection 방식으로. |
 |
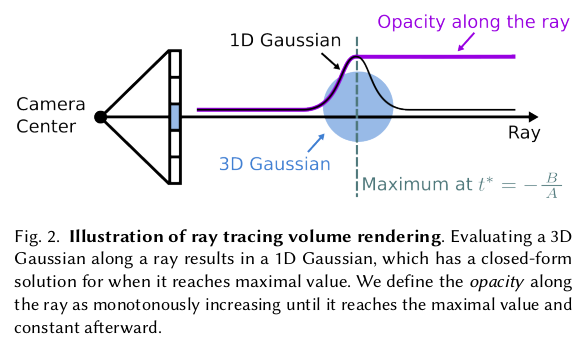 아까 했던 얘기랑 똑같은 얘기. ray를 따라 적분해나가면서 surface를 찾을 것인데, 3DGS 내부의 어떤 점 t를 샘플링했다면 해당 t가 3DGS내에서 갖는 opacity 값을 사용하면된다. t가 중심을 넘어간 위치라면 최대값으로 뱉어서 이후 계산 과정에서 무의미하도록 만들고. ray 위의 점 t에 여러 3DGS가 있을 수도 있는데, 이 경우에는 가장 작은 값을 사용했다고 한다. |
 |
학습 과정에서는 loss가 몇개 추가되면 위 formulation으로 mesh surface를 뽑아내는데 더 유리한 형태로 수렴한다고 함. 첫번째는 같은 ray상에 있는 gaussian끼리는 중심이 서로 같도록 유도하는 것. 다시 말해 surface에만 3dgs가 있어야 하니까 일단 한 곳으로 모이게 하는 것. 이 때 앞에있는 것과 뒤에있는 것 간의 가중치차이는 있어야 하니 blending weight를 앞에 곱해준다. ---------------- 하나 주의할 점은 blending weight도 결국 3DGS primitive로부터 뽑아낸 값이기 때문에 3DGS primitive가 값이 달라질수가 있다. 다른 말로 blending weight로 인해 엄한 3DGS opacity가 높아질수가있다. 따라서 gradient를 끊어줬다. |
  |
 depth가는데 normal 따라간다고. normal도 loss로 걸어주면 좋음. 근데 이게 좀 어려운게 3DGS는 결국 타원체기 때문에 normal이 고르지 않음. 방사형으로 뻗어나가는 normal을 갖고 있어서 smooth한 normal을 표현하기가 매우 어려움. (달걀을 갖고 평면을 표현하려는 것과 비슷) 그래서 3DGS의 normal을 그대로 사용하면 normal consistency가 큰 도움이 안됨.-> approximation 해서 normal이 도움되도록 변경 1) 3dgs를 타원에서 원으로, 방향도 xyz 같도록 normalize함 2) ray를 법선으로 갖는 plane 생성, 그리고 뒤집기 3) plane's normal을 unnormalize 이렇게 하면 3DGS이 타원체건 말건 결국 ray 진입각, 3dgs의 회전상태에 따라 normal이 결정되므로 normal이 일정하게 표현됨. |
  |
마지막으로 densification에서 손을 대는데, 기존에는 position gradient의 크기 기준을 정할 때 그냥 sum이었음. 근데 이건 생각해보면 한 픽셀에 걸리는 gradient가 여러 3DGS에 의해 결정되는데, 하나는 밀고 하나는 당기면 분명 변화가 필요한 픽셀이지만 sum으로 보면 0이기 때문에 변화가 없다. 따라서 sum을 할게 아니라 크기의 sum으로 해야된다는게 저자들의 주장. |
 결과보면 꽤나 의미가 있는 듯함. |
|
  |
최종 단에서 3DGS to mesh 하는 방법 3DGS 중심, 그리고 이를 둘러싸는 bounding box 점 8개 = 총 9개 point를 각 3DGS마다 생성한다. 그리고 나서 tetra hedral grid 생성하는 알고리즘을 돌림. 이렇게 하면 전체 공간을 둘러싸는 voxel이 아니라 실제 3DGS가 존재하는 공간만 감싸는 불규칙한 tetrahedral grid가 생성됨. 여기다가 marching tetrahedral을 갈기면 mesh가 나온다. |
 |
하나 문제는 grid를 형성하고 있는 vertex 중에 3DGS 중심에서 뽑힌 애들은 opacity가 있지만 bounding box 출신들은 opacity 값이 없음. 이를 추출하기 위해서 vertex를 이미지로 내려찍고, 해당하는 픽셀에 개입하는 3DGS를 모은 다음 거리 기반으로 모든 opacity를 계산한 뒤 최솟값을 할당했다고 함. |
 |
marching tetrahedral 갈길 때, 그냥 하면 linear 가정으로 하기 때문에 좀 각진 mesh가 나올 수도 있음. 이를 완화하기 위해서 한 edge에서 bineary search 8번, 최대 256개 위치를 뒤지면서 가장 적합한 위치를 찾아서 사용했다고 함. 이건 marching 알고리즘을 정확히 몰라서 이해 못함.  |
 디테일이 많아서 그런지, NeuS보다 좋음. 되게 고무적인듯. |
 |
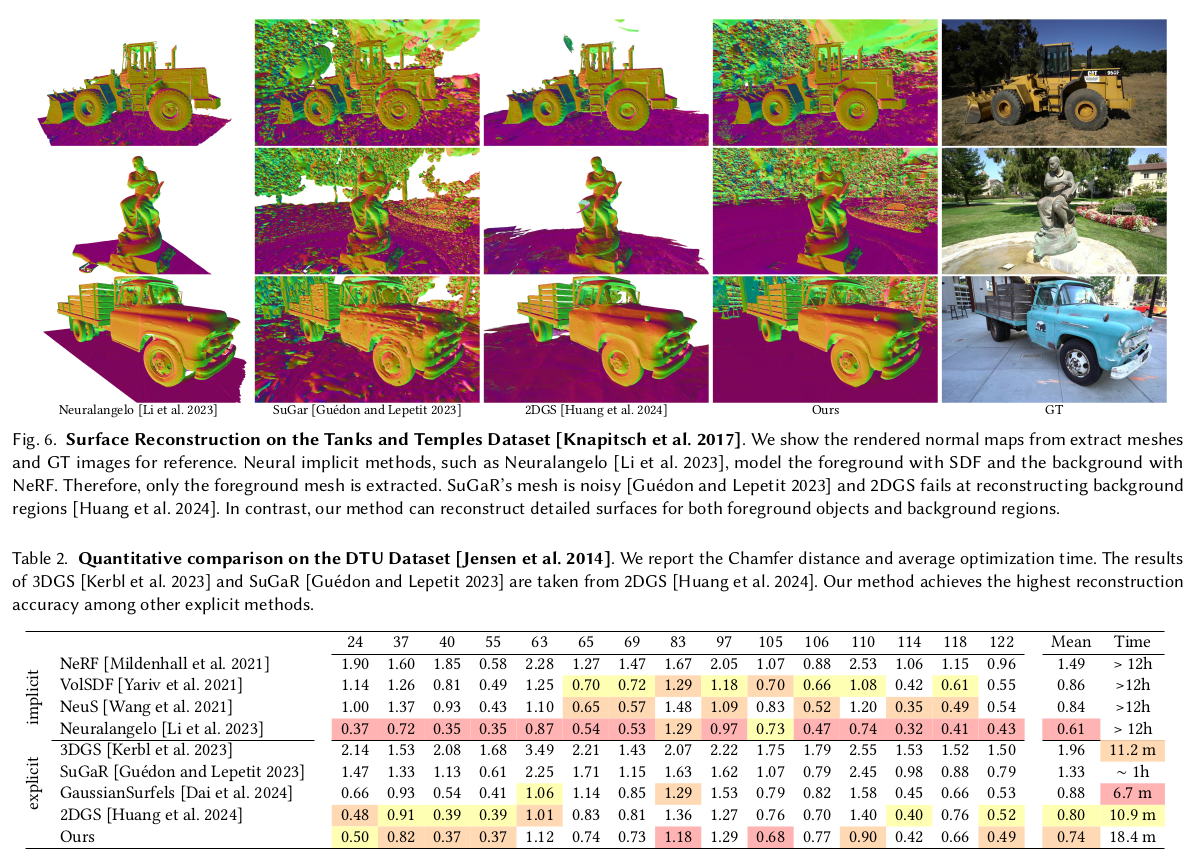 |
 |
반응형
'Paper > 3D vision' 카테고리의 다른 글
| π 3 : Scalable Permutation-Equivariant Visual Geometry Learning (pi3) (0) | 2025.08.13 |
|---|---|
| Deformable Beta Splatting (0) | 2025.06.09 |
| Large Steps in Inverse Rendering of Geometry (0) | 2025.04.29 |
| Towards Realistic Example-based Modeling via 3D Gaussian Stitching (0) | 2025.04.18 |
| SeamlessNeRF: Stitching Part NeRFs with Gradient Propagation (1) | 2025.04.16 |