반응형
*13강은 퀴즈 해설 강의로 제외함
Lecture
Lecture 14: Orthogonal vectors and subspaces | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note

- vector의 orthogonality test는 보통 dot product 결과가 0임을 확인하는 방식으로 진행된다.
- 직각 삼각형에서 가로변을 x, 세로변을 y로 보았을 때, 직관적으로보든 피타고라스 정리에서 유도해서 보든 x.T y =0 라는 식에 도달하고 이 사실이 확인되면 orthogonality를 알 수 있다.
- 이러한 방식은 고차원 subspace에서도 사용된다.

- subspace의 orthogonality를 확인하기 전 subspace가 orthogonal하다는 것의 정의는 위와 같다.
- 단순히 geometry가 orthogonal하다는 것과 다르다. 예를 들어, 벽과 바닥이 수직이라고 해서 벽과 바닥에 존재하는 모든 방향의 벡터들이 서로 수직한 것은 아닌 것과 비슷한 느낌이다.
- 위 정의를 만족해서 subspace 간의 어떤 벡터를 매칭해서 비교를 해도 dot product 값이 0이 나올 때 비로소 subspace들이 orthogonal하다고 할 수 있다.
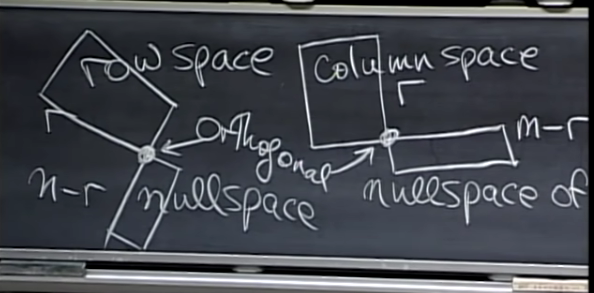
- row space와 null space는 orthogonal 하며 column space와 left null space는 orthogonal 하다.

- row space와 null space 먼저 생각해보면, Ax = 0 꼴을 보면 A의 row가 row space, x column이 null space를 나타낸다. 그리고 행렬의 곱 과정을 분해해보면 각각 dot(row of A, x) 의 형태로 계산되는 것을 알 수 있다.
- 즉, row of A와 null space x는 dot product 결과로 0을 만들어내게 되는데 이는 서로 수직함을 의미한다.
- "모든" 벡터에 대해 성립해야 하니 linear combination에 대해서도 0이 되는지 봐야 하는데 위 사진 좌측 하단과 같이 scalar를 곱하고 더하는 것 따위가 0이 되는 것을 바꾸진 않으므로 row space와 null space는 수직하다.
- column space와 left null space 역시 같은 원리로 A.T y = 0으로 생각하면 바로 알 수 있다.

- 차원에 대해서도 유념해야 한다. 예를 들어 3차원 공간에서 row space가 1차원 라인이고, null space가 1차원 라인인 상태가 존재할 수 있을까? 아니다.
- dim(C(A.T)) = rank, dim(N(A)) = n-rank 이다. 그러므로 row space가 1차원 라인이라면 null space는 2차원 평면이어야 한다.
- 이렇게 orthogonal한 subspace는 두 차원을 합했을 때 공간 전체 차원과 같아야 하기 때문에 서로 "complement"라고 표현한다.
- 전체 N 차원 공간에서 M 차원 space S가 있다면, 이와 complement한 orthogonal space T는 S와 수직한 N-M 차원 모든 벡터가 표현하는 subspace이다.

- 강의의 마지막은 다음 강에서 설명할 Ax=b의 해가 존재하지 않을 때 억지로 푸는 방법에 대한 소개다.
- Ax=b가 솔루션을 갖지 않을 때, 최대한 근사된 해를 계산하는 방법은 A.TA x = A.T b 와 같은 형태로 푸는 것이다.
- 여기서 A.T A가 invertible할 경우 양변에 inverse를 위해 xhat을 구할 수 있다.
- 왜 저렇게 푸는 것이 근사된 해를 구하는 방법인지는 뒤에 더 설명이 나올 것 같다.
- 그전에 나의 직관적 해설을 더하면 x= (A.T A).inv A.T b 로 푸는 것 자체는 Ax=b의 해가 있든 없든 둘 다 수학적으로 정확한 방법인 것은 맞다. 이상적이라면 이 방법을 통하면 근사된 해가 아니라 정답이 나오는게 맞다.
- 근사된 해가 나온다는 것의 의미는 실생활에서 에러가 존재하는 데이터로 풀 때 발생하는 것이다.
- Ax=b가 해가 없으면 invertible하지 않기 때문에 위 방법으로 안 풀린다. 하지만 실생활에서 A에 noise가 존재할 경우, nosie로 인해 invertible 해지는 경우가 빈번하게 생기는데 이러면 noise가 반영된 해가 나오므로 근사된 해가 나온다고 볼 수 있는 것이다. (음... 설명이 조금 아쉽긴 하지만 뒤에 나오니 넘어가자.)

- 요약하면 다음 강의로 넘어가기 전에 알아햘 것은 위 사진이 담은 내용이다.
- A.T A와 A가 같은 null space를 갖는다는 것. (A.T A x =0 , Ax=0의 null space는 같은게 당연하다.)
- 그리고 A.T A의 inverse 여부를 아는 것.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 16. Projection matrices and least squares (0) | 2023.01.21 |
|---|---|
| [Linear algebra] 15. Projection onto subspaces (0) | 2023.01.21 |
| [Linear algebra] 12. Graphs, networks, incidence matrices (0) | 2023.01.13 |
| [Linear algebra] 11. Matrix spaces, rank 1, small world graphs (0) | 2023.01.13 |
| [Linear algebra] 10. The four fundamental subspaces (0) | 2023.01.11 |