반응형
내 맘대로 Introduction
2021년 나온 논문이긴 한데 Facebook에서 낸 논문으로 아직까지도 잘 인용되는 논문. transformer 구조의 연산량 문제를 해결하는 구조 제안 논문이다.
핵심 아이디어는 NxN self-attention이 겪는 quadratic complexity 문제를 Nxd 수준의 linear complexity 문제로 바꾸는 방법이다. 토큰 개수가 늘어날수록 연산량이 제곱배로 증가하기 때문에 보통 transformer는 이미지 해상도를 제한할 수 밖에 없는데 이 논문은 high resolution 이미지도 transformer로 처리할 수 있도록 self-attention을 변형했다.
아이디어가 간단하지만 굉장히 좋다고 생각한다.
메모
  |
기본적으로 self-attention은 token 개수에 제곱배 연산량을 갖는다. 따라서 N이 커질 시 연산 속도 뿐만 아니라 메모리 사용량도 문제가 심각함. 따라서 이미지 해상도를 낮추거나, patch size를 키우는 등 token 개수를 낮추기 위해 어느 정도 손실을 감안해야 한다. |
 |
여기서 저자들은 self attention에서 NxN matrix가 나오는 QK.T 부분에 집중했다. Q와 K는 각각 Nxd dimension 인데 이를 그냥 단순히 둘다 X라고 보면, Gram matrix (NxN)을 계산하는 모양이다. 이 순서를 바꿔 K.T Q로만 바꿔 gram matrix 대신 covariance matrix로 계산하면 dxd 를 계산하는 모양이 되므로 연산량이 폭발적으로 준다. 이 때 gram <->cov matrix 사이는 같은 eigenvector로 변환이 가능한 사이로 밀접하게 연관이 있다. determinisitc하게 엮여있기 때문에 gram matrix를 찾는 것이나 cov matrix를 찾는 것이나 사실 같은 문제를 푸는 것. 이 점에 착안해서 저자들은 QK.T -> K.T Q로 뒤집는 방법을 제안한다. |
  |
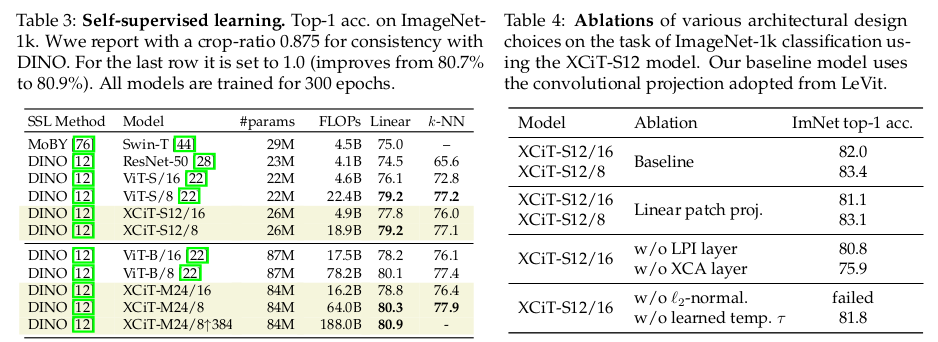
아주 단순한 아이디어고, 뒤집기만 하면 끝이다. 근데 실험적으로 안정적 수렴을 위해 2가지 장치를 추가했다. 첫번째는 q와 k Nxd Token들에 대해서 d 차원을 l2 normalization했다. (합 크기 1) 이렇게 안하면 N이 늘어났을 때 안정성이 떨어지는 것을 보았다고 함 두번째는 l2 normalization으로 작아진 크기를 자체적으로 보상하기 위해서 learnable temperature (scale factor)를 추가해준 것. |
 |
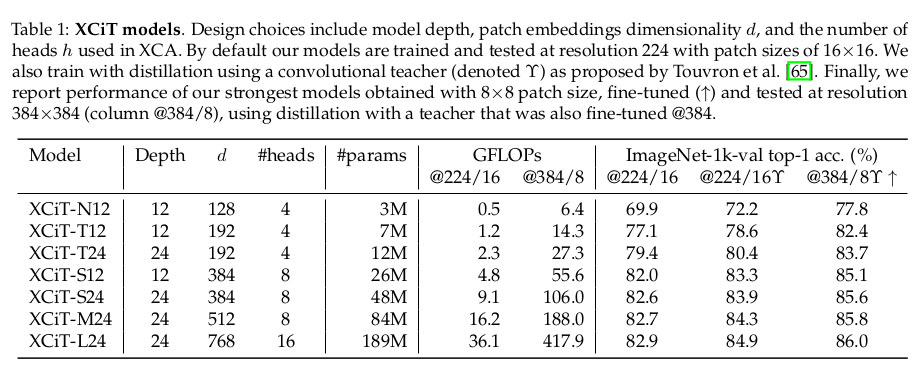
q와 k를 뒤집은 것일 뿐이므로, multi head 구현도 문제없다. 기존과 똑같이 head를 여러개 두어서 K.T Q를 반복하면 됨 다만 이렇게 되면 학습 안정성이 조금 떨어지는 현상이 있어서, head를 늘리면 q,k의 dimension을 같은 비율로 줄여줬다고 한다. ---결과적으로 NxNxd -> Nxdxd로 낮춰진다. N>>d인 상황에서 매우 유용한 연산량 감소다. |
 |
|
 |
위 XCA 를 추가해서 transformer block을 구성할 땐 layer norm와 LPI, FFN을 추가했다. 1) LPI depth wise convolution + BN + GELU 2) FFN point wise MLP (1x1 conv) |
 |
positional encoding은 쿨하게 sin-cos으로 끝. learnable로 하면 interpolation했을 때 성능감소도 있고 나중에 튜닝해야 할 가능성이 생기는데, 연산량도 줄였겠다. 그냥 모든 patch에 다 명시적으로 때려박아서 사용했음. |
  |
|
   |
반응형
'Paper > Others' 카테고리의 다른 글
| ArcFace: Additive Angular Margin Loss for DeepFace Recognition (0) | 2024.10.07 |
|---|---|
| Improving 2D Feature Representations by 3D-Aware Fine-Tuning (0) | 2024.09.11 |
| SHIC: Shape-Image Correspondences with no Keypoint Supervision (0) | 2024.07.30 |
| As-Rigid-As-Possible Surface Modeling (0) | 2024.07.16 |
| FeatUp: A Model-Agnostic Framework for Features at Any Resolution (0) | 2024.05.13 |