반응형
내 맘대로 Introduction

이 논문은 SMPL의 joint 구조를 실제 인간의 뼈구조와 일치시킨 논문이다. 쉽게 말하면 SMPL에 뼈를 추가한 것이며 뼈 또한 굵기, 길이가 파라미터로 조절될 수 있도록 했다. BSM 이라고 불리는 뼈 모델을 먼저 만들고 이것은 SMPL 기본 골격과 껴맞춘 뒤, 수 많은 피팅 결과들을 보면서 parameterization까지 마쳐서 SKEL 이라는 최종 모델을 만들었다.
특징점은 1) joint 위치가 뼈로 인한 위치로 변화했으므로 기존 위치와 많이 달라짐, 2) BSM 피팅 오차도 있어서 뼈가 튀어나오는 경우도 종종 있음 (완벽하게 혼연일체된 것은 아닌 것 같음) 이다.
shape(체형)과 뼈는 사실 살찐 정도에 따라 다를 수 있으므로 어느 정도 독립적인데 SKEL에서 그 부분을 표현할 수 있게 된 것은 확연한 진일보인 것 같다.
메모
 |
새로운 모델 SKEL은 SMPL과 같이 1) pose param, q에 조절되면서 SMPL param space를 공유함 2) shape param은 SMPL 공유함. 2) 먼저 뼈구조, 자유도를 고려해서 BSM을 만듦 3) BSM을 SMPL에 피팅하는 방법을 만듦 3) AMASS 데이터에 하나하나 피팅하고 결과를 보아서 parameterization함. |
 |
일단 SMPL recap. AMASS는 SMPL 피팅 결과들+ 모션이 섞인 방대한 양의 SMPL 데이터셋 |
 |
BSM ( 뼈다귀 모델) 1) 24개 뼈로 구성됨 2) scale , pose param으로 통제됨 - scale은 3자유도, 길이, 굵기 + @ - pose는 총 46 자유도, 개수가 독특한 건 관절마다 자유도가 다르기 때문임. 어깨 vs 무릎 생각하면 이해됨. 3) BSM_J는 뼈마디가 맞닿는 joint의 위치를 계산 4) BSM_V는 뼈 하나하나 mesh를 구성하고 있는 vertex 위치 계산 5) m0로 표시되는 것은 marker로 뼈 위에 지정된 마커 위치임. - 마커 위치를 봐야 뼈의 회전을 잘 알 수 있음. 6) BSM_M는 마커의 위치 계산 BSM은 크게 하체 척추 어깨 팔목으로 나뉘어 있음. 이 부분들은 단순히 뼈 1개가 아니라 독특한 구조들을 갖고 있어서 별도로 모델링 수행함. |
  |
하체는 누가 만들어 놓은 것 갖다 씀.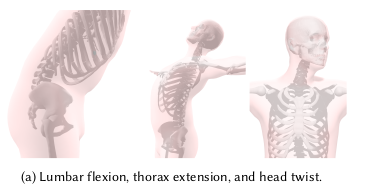 척추는 신전, 뒤틀기 같은 모션이 표현 가능해야 하는데 척추 1개 1개를 따로 모델링하면 이게 힘들다. 연결된 구조라는 특징을 살려서 표현했다. 연결되어 있기 때문에 자유도가 1개 적다.(디스크끼리 축회전하는 일은 없다.) 따라서 기울어진 각도만 표현할 수 있는 xzy euler angle로 척추 뼈 1개 1개 관계를 모델링 했다. 다르게 말하면 기울어진 각도 + 뼈길이를 알면 경추부터 요추까지 위치를 표현 가능. |
 |
어깨도 가져다 씀. 최고 복잡한 관절이라서 기존 자료를 가져오지 않고서는 computer vision 범위를 넘어서는 듯. (실제로 저자 중 한국인은 근골격계 연구실 출신임...) 팔목을 따로 한 이유는 팔목에 뼈가 1개이기 때문임! 만져보면 2개다. 닭날개처럼. 새끼손가락 쪽에 있는 ulnar 좀 작은 뼈는 상완골에 직접 붙어 있는 뼈라서 회전할 때 별로 안움직임. 그래서 엄지 쪽에 있는 radius의 회전만 표현할 수 있도록 파라미터를 잡았다고 함. 주의! BSM도 피부 surface 있음. |
  |
내용은 감추어져있지만 위에 설명한 것을 바탕으로 BSM을 어찌 잘 만들었고 이젠 이것을 SMPL과 엮는 일이다. 피팅을 제일 먼저 해야하는데 BSM joint와 SMPL joint는 완전 다름. 위치부터 개수까지. 피팅하려면 둘 간의 연결을 먼저 지어야 함. joint를 직접 매칭하는건 포기했고 피부 vertex 간의 correspondence를 맞추기로 함.  1) BSM surface vertex 중에 skinning weight를 보았을 때 각 뼈가 가장 영향을 크게 받는 vertex를 선별함. (사실 상 뼈 1개 움직임에만 dependent한 vertex가 어딘지 찾아서 bony marker로 지정) - 이렇게만 맞추면 살찐 사람 피팅할 때 너무 불리함 - too sparse 하기도 2) 그래서 soft marker라고 살 위에서 추가로 48개 지정해서 사용함 (이건 대충 고르게 찍은 것 같음. 어떻게 골랐는지 안나옴) |
    |
soft marker가 의미가 있으려면 살찐 정도에 따라서 어떻게 marker가 움직이는지 파악이 가능해야 활용이 가능하다 즉, shape param에 따라 soft marker의 offset이 어떻게 발생하는지 알아야 한다. 이게 쉽지 않으니까 이번엔 OSSO라는 bone+ skin (controlled by shape param)모델을 활용했다.  1) BSM softmarker 지정 2) OSSO를 BSM과 뼈 algin으로 맞춤. 3) OSSO soft maker 지정 (가장 가까운 mesh face) 4) AddBiomechanics 툴을 이용해서 AMASS에 OSSO 피팅 5) 피팅 결과를 -> BSM으로 전달. 6) BSM parameterization. 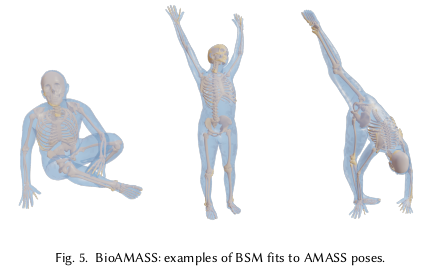 |
 |
마지막으로 BSM->SMPL까지 연동해서 SKEL 모델로 정리. 1) SMPL T-POSE와 BSM T-POSE를 일단 맞춤 (일종의 파라미터 초기값을 맞추는 것, zero param이 T-pose로 일단 같게) 2) BioAMASS (아까 BSM -> SMPL 피팅 끝난 데이터셋) 갖고 이번엔 파라미터 관점에서 엮는다. |
 |
먼저 SMPL vertex - > fitted BSM joint로 갈 수 있는 new joint regressor를 하나 구해야 함. 이것 SMPL에도 있으니 그 방법 그대로 사용. 여기까진 쉬움.  어려운건 bone rotation임. SMPL -> BSM bone 상태도 알아야 함. joint 위치를 안다고 뼈의 회전 상태를 알 순 없음. 축회전은 특히. 따라서 SMPL shape param ( bone 상태는 SMPL pose param 갖고는 알 수 없으니 pose와는 독립적, BSM pose 아님) 으로부터 bone rotation을 찾는 방법도 찾아두어야 함. 일단 회전 표현 차이를 알고 있어야 함. SMPL은 pelvis를 기준으로 잡고 T_pose 일때 모든 관절의 rotation이 같은 좌표계로 정렬되어 있음. (위 그림 제일 오른쪽) 근데 BSM은 뼈마다 좌표계가 따로 있음. ----------------------------- 뼈는 자세가 바뀌어서 크게크게 움직이는 R_base와 뒤틀림이나 뼈 고유의 회전을 표현하는 R(shape)으로 나누었음. |
 |
 무슨 말인지 차이는 위 그림을 보면 단번에 이해됨. 이렇게 정의한 뒤, BioAMASS를 다시 활용해서 SMPL(pose, shape) <-> Bone rotation 간의 parameterization을 함. |
   |
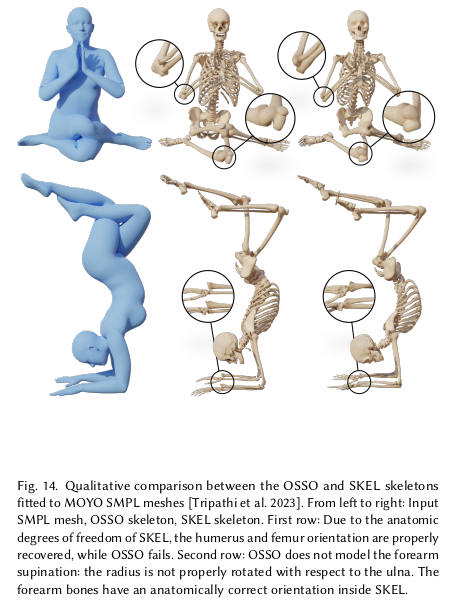
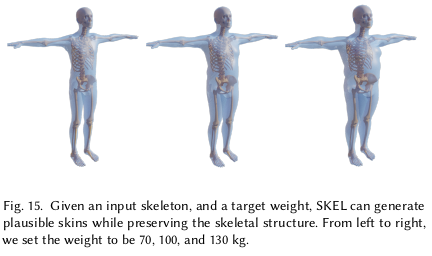
뼈의 축회전이 표현이 가능해짐에 따라 pose dependent shape도 업데이트가 되긴 해야 했다. 뼈가 회전할 수 있음을 반영하지 않으면 위 그림과 같이 됨. 기존에는 pose가 변화시키는 shape은 팔 비틀기 같은건 고려를 애초에 안했기 때문. 그래서 새로운 pose, q + shape을 갖고 skin 찾는 matrix를 새로 계산함 (수식5) 수식 (6)처럼 복잡해진 이유는 앞서 짧게 언급한 바와 같이 뼈 고유의 좌표계가 있기 때문 수식(6) == (뼈 고유좌표계로 바꾸기)변환( 공유 좌표계로 바꾸기) |
  |
joint도 뼈 모양이 이제 선이 아니라 부피를 갖는 3차원이므로 new pose, q 처럼 뒤틀림이 있는 경우 움직일 수 있다. 따라서 shape dependent joint 를 계산하기 위해 수식(7)로 피팅 ---------- 뼈 자체도 vertex를 갖고 있으므로 pose, shape dependent bone vertex 얻을 수 있게 수식(8)로 피팅 |
 |
 |
 |
 |
 |
반응형
'Paper > Human' 카테고리의 다른 글
| GPAvatar: Generalizable and Precise Head Avatar from Image(s) (0) | 2024.04.17 |
|---|---|
| StructLDM: Structured Latent Diffusion for 3D Human Generation (0) | 2024.04.17 |
| Drivable 3D Gaussian Avatars (0) | 2024.02.18 |
| Gaussian Head Avatar: Ultra High-fidelity Head Avatar via Dynamic Gaussians (0) | 2024.02.17 |
| Rig3DGS: Creating Controllable Portraits from Casual Monocular Videos (0) | 2024.02.13 |
