반응형
내 맘대로 Introduction
이 논문은 DDPM의 분석 보고서라고 볼 수 있다. DDPM이라는 논문에서 제시한 파라미터 하나 하나를 뜯어보면서 어떻게 바꿨을 때 향상이 있었는지 보여주고, trade-off 관계가 있다면 경향이 어떤지 보여주는 논문이다. 정말 보고서와 같은 논문인다. 핵심적인 아이디어는 따라서 없다.
사실 이제는 쓸모 없는 내용도 많아서 그냥 대충 읽어도 될 것 같다. 말이 너무 많다ㅠ
메모하며 읽기
 |
  |
| DDPM을 분석하는 논문답게 DDPM 수식을 상당히 자세하게 recap하고 시작한다. | |
 |
  |
| 첫번째로 주목한 점은 DDPM 은 reverse process distribution을 찾아나갈 때 mean 값만 집중하지 std값은 특정값으로 가정해버리면서 버린다는 점이다. (실험적으로 특별하지 않았기 때문에) | |
 |
 |
| generation 모델에서 사용하는 대표적 metric인 log-likelihood가 DDPM std 값에 덜 민감하다는 의미인데, 왜 덜 민감한지 알아내고 분석하는 것이 성능 향상의 열쇠라고 주장한다. (왜냐면 log-likelihood를 조금만 손대도 다른 알고리즘들은 성능이 뛰었기 때문이다. DDPM도 조금만 손대서 std에 민감하도록 수정할 수만 있고 학습만 잘 시키면 같은 맥락으로 DDPM도 성능이 뛰지 않을까 라는 기대 같다.) | |
  |
  |
 |
 |
| 일단 DDPM에서는 sigma를 beta 혹은 beta'로 가정해서 사용하는데 이 둘 간에 성능에 성능 차이가 없었던 이유는 분명하다. 위 그림은 보면 모든 time step에 대해서 beta, beta' 비율을 추적한 것인데 애초에 학습 초기가 아니면 웬만하면 둘 값이 같기 때문이다. 게다가 T가 클수록 그 차이는 더 빠르게 줄어든다. 따라서 sigma를 beta로 쓰냐 beta'으로 쓰냐는 애초에 의미가 있을 수가 없음. |
그렇다고 하나로 퉁치는게 낫냐? 그건 아니다. Variational lower bound (VLB) 커브를 보면 sigma가 학습 초기 구간에 diffusion process에 큰 영향을 미친다는 것을 알 수 있다. 그러므로 beta, beta' 를 아주 섬세하게 조율해서 최적 sigma를 찾아내는 것이 중요하다는 것이다. 따라서 여기선 learnable parameter, v를 추정하도록 해서 네트워크가 알아서 조정하도록 자유도를 열어 주었다. |
  |
 |
 |
 |
| noise를 주는 방식도 beta를 linear하게 조절하는 방법에서 cosine 형태로 주는 방법으로 교체하는게 낫다고 설명한다. noise를 이미 충분히 많이 줘서 N(0,1)에 가까운 레벨이라면 beta가 크건 작건 사실 큰 영향이 없을 것이다. 어찌 됐든 이미 N(0,1)이니 |
실제로 T에 가까운 몇 구간은 건너 뛰어도 별 차이가 없다. noise 조금 더 준거나 안준거나 T에 가까우면 비슷하다는 점이다. 네트워크가 되도록 모든 noise 더하는 구간에 의미를 충분히 갖도록 초반부와 후반부에는 noise를 조금, 중간에는 많이 줄 수 있도록 cosine으로 beta를 조절하는 것이 좋다고 소개한다. |
  |
  |
 |
 |
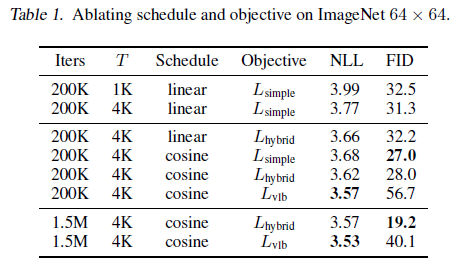
| sigma를 적극적으로 고려하도록 loss까지 추가하니 추가적으로 하나 이슈가 발생했는데 loss의 불안정성이 높아진 것이다. | 이를 해결하기 위해서 VLB loss만 따로 측정해서 어떤 time stamp가 큰지 관찰해서 찾아낸 다음. 수식(18)과 같이 loss가 큰 time stamp에서는 loss가 scale down될 수 있도록 L/probability로 regularization을 가해줬다. |
 |
 |
 |
 |
 |
   |
 |
 |
| sampling step을 어떤 크기로 조절할 때 성능 하락이 적은지 여러 케이스 스터디를 해뒀다. | DDIM 방식에서는 이런 sampling step 조절 방식 함부로 적용하면 오히려 망가지니 DDPM에서만 쓰라고 한다. (DDIM에는 수식적으로 다르게 할 수 있으니 그 방식대로 해야 함) |
  |
 |
| GAN보다 당연히 좋다는 걸 숫자로 강조해서 보여줌 | |
  |
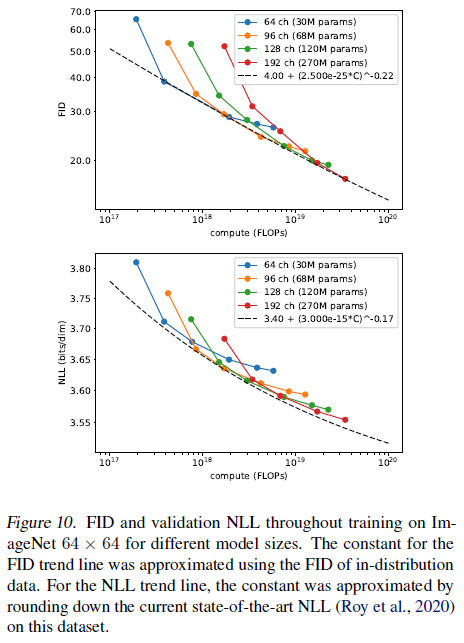 |
| 모델 파라미터 수에 따라 성능 차이 케이스 스터디도 해뒀음 |
반응형