반응형
내 맘대로 Introduction

이 논문은 DDPM이 전개한 식 (w/ Markov chain 가정)을 관찰한 결과, non-Markovian 식으로도 전개할 수 있다는 것을 발견하고 식을 정립한 논문이다. 이전 time stamp만이 현재 time stamp 결과를 결정하는 관계 (markovian)에서 원본 이미지 + 이전 time stamp가 현재 time stamp를 결정하는 관계로 모델링하면서 문제를 다르게 풀었다.
이 논문이 역작으로 꼽히는 이유는 모델링 방법을 바꿨음에도 수식을 전개하다보면 결국 DDPM과 같은 결론을 얻게 된다는 것을 증명했고, 본인들이 전개한 식의 특수 케이스가 DDPM 식이라는 것도 밝혀냈다. 한마디로 DDPM을 부분 집합으로 보게 만들어 버릴만한 더 큰 집합을 찾아낸 것이다.
새로운 식의 의미도 풍부한데, 더 성능을 끌어올릴 가능성을 높였고 속도 문제도 해결할 수 있게 되었다. 한마디로 DDPM 상위 호환 논문이다.
메모하며 읽기
  |
| DDPM은 수식(1)과 같이 forward든 backward든 markvian을 가정한다. t-1 과 t 만으로 기술된다. markovian 가정을 했기 때문에 수식(3)과 같은 reverse process에 대한 식 정립이 가능했던 것이다. |
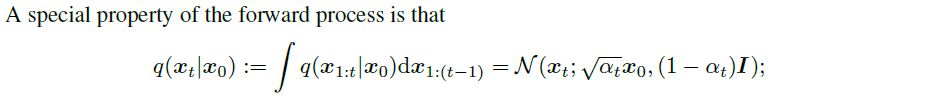  |
| error만 minimize하면 되는 문제로 간소화될 수 있음도 markovian 가정으로 인한 것이라 볼 수 있다. ---- variance는 1로 고정해서 크게 고려하지 않는 가정은 추가로 기억해둘 만하다. |
 |
| 별개로 DDPM이 iteration 수 T가 고정되어 있어 느린 속도 문제가 있다는 점을 짚어주고 논문을 시작한다. |
 |
| DDIM에서는 앞서 언급한 markovian 가정을 사용하지 않고 새로운 모델을 제시한다. |
  |
| 위 수식(8)과 같이 time, t를 결정하는 요소는 time t-1 뿐만 아니라 noise가 섞여있지 않은 원본 t=0도 같이 있다고 모델링했다. 역시나 분포 자체는 gaussian을 사용하는 것은 동일하므로 q(1:T | 0) marginal distribution을 풀어 보면, bayes rule에 따라 수식(6)과 같이 변형된다. 원본 x0 까지 포함되는 것이 무슨 차이냐고 할 수 있지만, 그냥 이렇게 해볼까? 해서 한게 아니라 사실 수학이 숨어있다. |
 |
| 수식(8)에서 시작하면 기존에 reverse process에서 찾아야 하는 mu, std 값이 수식(9)과 같이 새롭게 정의된다. 주목할 점은 분명 다른 모델링으로 출발했음에도 수식(9) 안에 존재하는 trainable parameter는 e(x) 뿐이라는 점이다. 다시 말해, 수식이야 달라졌지만 네트워크가 찾아내야 하는 값은 여전히 e(x) 하나이고 loss도 e(x)로만 세워지면 충분하다는 것이다. DDPM과 약간의 term이 붙을 뿐 무시한다면 핵심이 완전히 100% 동일하다는 점이 중요하다. |
 |
| 약간의 term이 붙은 부분은 조절해서 DDPM에서 말하는 gamma parameter과 값을 맞출 경우 DDPM과 100% 동일해지므로, DDIM의 특수 케이스가 DDPM이라는 결론을 얻을 수 있다. |
 |
| 더 인상적인 점은 gamma=1 맞아떨어지도록 설정한 DDIM을 가정한다면, 이미 학습 완료된 DDPM을 DDIM으로 가정해서 sampling하는 것이 가능하다. (특수 케이스 이므로 저 큰 범위이인 DDIM 식이 안 통할리 없다.) |
 |
| 이미 학습 완료된 DDPM 모델을 갖고 와서 sampling을 할 때, 우리가 익히 아는 수식(4)와 같이 sampling해서 이미지 생성을 해도 되지만 수식(12)과 같이 DDIM 식으로 sampling해도 된다. ------------------ 또 하나 주목할 점은 저 sigma_t를 0 으로 둘 경우 수식(12) 전체 수식에서 randomness가 사라지는 모습을 볼 수 있다. 이 말인 즉 sigma를 0으로 설정하고 학습한 DDIM의 경우 latent space와 결과물이 1대1 대응으로 결정된다는 것이다. 같은 latent를 고르면 같은 결과가 나오는 deterministic한 특성을 갖게 할 수도 있다. (이런 특성을 추가할 수 있도록 DDPM이 확장되었다는 의미) |
  |
| (여긴 수학적으로 완전히 이해하지 못했다.) 또 다른 추가 점은, 기존 DDPM은 time stamp 건너뛰기가 안됐다. 왜냐면 직전 time stamp만이 다음 time stamp를 결정하기 때문이다. 하지만 DDIM의 경우, x0가 모두에게 share 되어있으므로 x0을 기준으로 식을 전개해서 건너뛰기가 가능해진다. (직관적으로 보았을 때 DDIM이 DDPM보다 deterministic하므로, 건너뛰어도 맞출 가능성이 높아 보임) 이게 가능하다는 이야기는 inference할 때 시간을 줄일 수 있다는 말이다. |
 |
| 또 다른 말로는 학습 때 사용하지 않은 iteration 수 T여도 사용이 가능해진다는 의미다. 학습에서 사용한 T를 그대로 사용할 필요가 없어진다. |
 |
| 또 DDIM을 다른 시선으로 바라보면, q(t |t-1, 0) 로 모델링하는 방식으로 전개한 수식 (12)는 보다 deterministic한 식이고, linearize가 가능할 것이다. 즉 t-1에서 t로 가는 짧은 구간에 일어나는 변화가 linearize가 가능해지므로 Ordinary differential equation풀 둣이 t-1, t 간의 변화 과정을 직접 계산할 수 있게 된다. interpolation이 용이해진다는 것이다. interpolation이 가능하다는 점은 그 구간의 변화가 tracking이 된다는 것이고, 다시 deterministic하다는 것이다. 이러한 특성을 믿고 보면 DDIM 중간 산물들은 이미지 embedding으로 바라볼 수 있을 정도로 fixed value 특징을 충분히 갖고 있다고 할 수 있다. |
 |
| 여태까지 deterministic하다는 것을 다시 보면, 수식(12)에서 sigma_t가 0이라는 가정이 있어야만 가능했던 것인데 0이 아니어도 풀려는 시도가 있다. stochastic differential equation 수식을 가져와서 randomness를 포함해서 풀려는 연구도 등장했다고 소개해준다. |
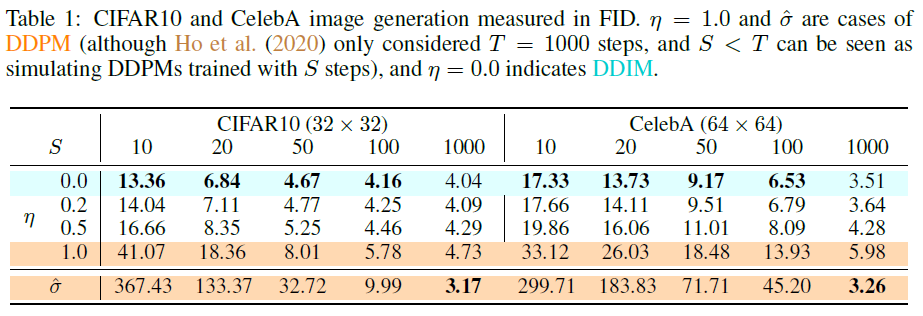 일단 FID 성능이 DDPM 대비 더 적은 iteration임에도 더 뛰어나다는 점을 보여줌. |
 |
 |
 |
 |
 |
반응형