PhysGaussian: Physics-Integrated 3D Gaussians for Generative Dynamics

내 맘대로 Introduction

 

개인적으로 역작이라고 생각하는 논문이 나왔다. 기계공학에서 접했던 mechanics 수식을 이용해 학습 완료된 3d gaussian은 simulation하는 논문이다. 컨셉은 dynamic 3D GS 같이 느껴지지만 time 축에 따라 학습을 추가로 시키는 것이 아니다. static 3D GS를 만드는 것까지는 기존 논문과 아무런 차이가 없고 그대로 사용하되, mechanics를 이용해 각 gaussian들이 힘을 받았을 때 어떻게 이동할지를 계산해서 time에 따른 변화를 "부여"하는 것이다. 학습이 아니라 직접 옮기는 방법이다. 진짜 시뮬레이션.

 

따라서 데이터를 추가로 video로 얻을 필요도 없고 그냥 기존 3D GS처럼 데이터 얻고 학습만 시키면 끝이다. 시뮬레이션 방법론이기 때문이다. 이 논문은 project page 를 방문해보길 적극 추천한다. 영상을 보면 무슨 말인지 단번에 이해할 수 있다. 

 

핵심 아이디어는 contnuum mechanics, Material point method 등 어려운 말이 등장하지만 결국, 시뮬레이션에서 각 particle(여기선 gaussian)들에게 external force와 velocity를 부여하는데 이 값이 주어졌을 때 해당하는 particle(gaussian)이 어떻게 움직여야 하는지를 정립한 것이다. 위치가 움직이는 것 뿐만 아니라 자연스러운 렌더링을 유지해야 하므로 Spherical harmonic도 같이 회전시키는 트릭도 소개한다. 

 

내가 기계공학과 출신이긴 하지만 MPM은 이해못했다. 그냥 직관적으로 이해한 수준을 기록한다.

 

이 논문 코드 공개가 기다려진다.

 

메모하며 읽기

	전체 파이프 라인 그림인데  뭔가 복잡해보이지만 실제론 그냥 3D GS를 그려놓은 것이다.  1) optimization anisotropic loss term, gaussian kernel filling은 선택적인 것. 모양이 뾰족뾰족하면 움직였을 때 visual artifact가 생길 확률이 높으니까 되도록 동글동글하게 만들고 싶을 때나, 형상이 내부 공간이 넓어 빈 공간이 너무 많을 것 같을 때 임의로 채워주고 싶을 때 사용하는 기능들이다.  2) physics intergration 시뮬레이션하고자 하는 상황에서 발생하는 force, velocity에 따라 gaussian을 움직이는 과정.  학습과 전혀 무관하고 post processing이다.

3D GS recap이라 생략. dynamic 3D GS의 핵심은 position x와 covariance A를 time dependent하게 만들어내는 것.  다른 논문들은 video 입력으로 학습해냈지만, 이 논문은 수식으로 계산해낸다.

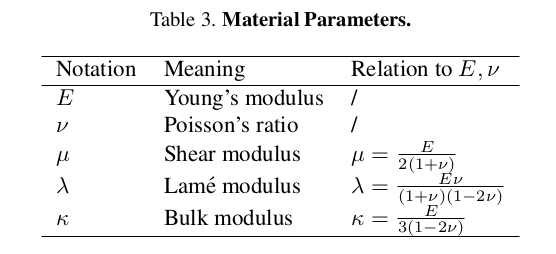
continuum mechanics 말이 어렵지만 결국 F = ma 라는 얘기다. 수식(3)을 보면 particle이 있을 때 해당 위치의 밀도와 가속도를 곱한 것(좌변)이 자체 힘(Cauchy stress) + 외부 힘 이라는 소리. 따라서 밀도와 속도(deformation gradient), 그리고 외부 힘(있다면)을 알 경우 particle이 어떻게 움직일지를 모델링할 수 있다. 알아야 할 것 1) 밀도 (임의로 지정 or 실제 물성치 입력) 2) deformation gradient (simulation으로 생성) 3) 외부힘 (simulation으로 생성) 사실 다 알고 있어서 이대로 particle (gaussian)을 옮기면 된다. ------------ 수식(2)같은 경우 그냥 밀도 자체는 시간에 따라 변하지 않는다는 소리 (배경지식)

이론적으로 수식(3)이면 움직일수 있는게 맞는데, 저자들이 사용한 MPM이라는 이론 기반 tool과 수식(3)을 연결 지으려면 한가지 수식 전개가 더 필요하다. 내가 직관적으로 이해한 바에 의하면 MPM이란 particle과 그것이 존재하는 공간 grid 간의 관계를 표현하는 방법이다. 쉽게 말하면 voxel grid가 존재하고 각 voxel grid가 어떻게 움직일지 속도, 가속도를 갖고 있을 때, 그 voxel에 들어있는 particle들은 어떻게 움직일지 approximation하는 컨셉 같다.  ---------- 수식(4)도 결국은 ma = F 인데 (voxel grid level 에서) ma = (particle level에서) F 자세히 보면 수식(3) 우변의 첫항과, 수식(4) 우변의 첫항이 매우 유사함을 알 수 있다. 다만 갖고 있는 voxel grid로 discretize돼야 하므로 voxel size, B spline kernel이 추가된 형태일 뿐이다.  ------------ 결론만 말하면 저자들이 사용한 시뮬레이션 툴 MPM에서는 voxel grid 단위로 속도, 힘을 다루는데 수식(4)를 이용해 particle로 존재하는 gaussian에 속도, 힘으로 변환할 수 있다.  ------------ 참고로 deformation는 elastic deformation, plastic deformation으로 나뉘는데 전자는 물체 특성에 의한 변형, 후자는 실제 이동, 회전에 의한 변형으로 볼 수 있다.  시간에 따라 이동하는 형상이라면 전자, 후자가 다 존재하겠지만 지금은 정적인 형상이 외부 힘에 의해 어떻게 변형되는지만 보고 싶기 때문에 elastic deformation만 있다고 가정했다고 한다. 같이 푸는 건 가능할지 모르겠음... 어떻게 분리할 수 있을까.

deformation이 어떻게 일어날지 수식(3) 수식(4)를 통해 계산할 수 있다고 할 때 이 deformation으로 어떻게 gaussian을 deformation할 수 있을까.  deformed position x를 기존 3D GS에 넣으면 끝이다.  하나 주의할 점은 deformation function이 linear하지 않을 수 있다. 즉, deformation된 후 공간이 왜곡돼있을 경우, deformed position을 대입한 수식(5)는 더 이상 3D gaussian이 아니라 찌그러진 어떤 distribution이 되어버릴 수 있다.  이를 해결하기 위해선 deformation function을 linearize해서 deformation 전후 공간이 똑같이 euclidean space에 있도록 해줬다.  그게 수식(6)의 의미다. deformation을 1st order approximation했다고 봐도 됨. 그러면 deformed position을 대입한 3D GS는 여전히 3D GS다.

수식을 정리하면 자연스럽게 가운데 껴있는 covariance도 deformation gradient가 전후로 곱해져 deformed covariance가 된다.  결론적으로 힘, 속도가 주어졌을 때 gaussian이 어떻게 움직여지고 모양이 변하는지 알 수 있게 된다. (time depedent, simulation dependent) ----------------------- MPM tool으로부터 particle level 힘 속도를 계산하기 위해 (수식(4)) 필요한 V0는 background cell (아마 임의로 잡은 voxel 크기) 를 그 안에 들어있는 particle 개수로 나눈 값을 사용했다.  밀도는 맘대로 정함.

particle(gaussian)을 움직이고 변형하는 것은 끝났다. 이제 렌더링할 때 변형 후에도 망가지지 않게 하는 것이 중요하다. 대처법은 변형할 때 gaussian이 회전했다면 이에 맞추어 SH basis function도 회전시켜주는 것이다. coefficient를 바꿀 순 없으니 말이다.  3D GS 원 저자 코드를 그대로 사용하고 싶은데, SH basis function을 회전시키려면 원저자 코드에 손을 대야했기 때문에 약간의 노하우로, 렌더링할 때 사용하는 ray( view direction)을 역으로 돌렸다고 한다. (구현적으로 머리를 잘쓴듯) deformation 을 알고 있을 때 이를 polar decompositino하면 rotation과 scale로 분리할 수 있는데, 여기서 나온 rotation inverse를 view direction에 곱해주어 마치 basis function이 회전한 것과 동일한 효과를 주었다. 수식(9)를 보면 view direction d에 곱해지는 것을 볼 수 있다. 이러면 원저자 CUDA코드(제일 수정하기 빡센...)를 건들지 않고도 똑같은 효과를 낼 수 있다.

Sec 3.5 에서 소개한 방법 말고도 SH basis function을 회전시키는 효과를 낼 수 있다.  computional fluid dynamics에서 개념을 가져왔다는데 잘 모르겠고 직관적으로만 보면,  어떤 particle에 부여된 가속도를 알 때 유체라는 가정하에 covariance가 어떻게 변형될지 계산할 수 있다.  covariance 변형 전, 후 값 중 scale은 버리고, rotation만 취할 시 수식(9)에서 사용할 R값을 얻을 수 있다.  ------------ 3.6의 의미는 deformation gradient를 계산한 뒤, polar decomposition하는 것 대신 covariance 전, 후 값만 갖고 rotation을 얻을 수 있다는 것이다. ------------ 개인적으로 유체라는 가정을 하기 때문에 연산량이 조금 크더라도 3.5 방식이 나을 것 같다.

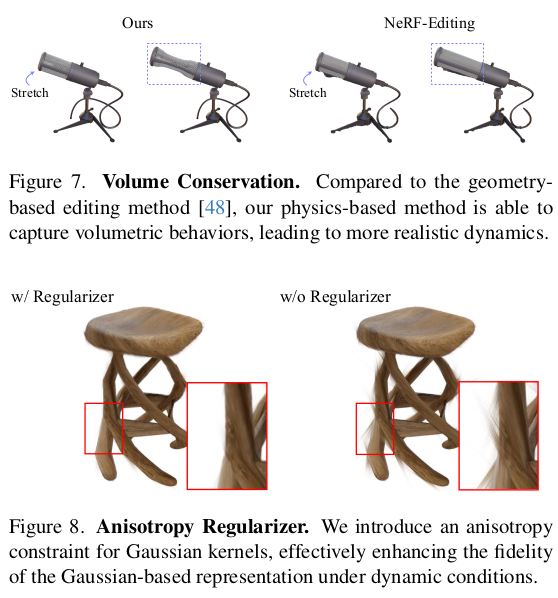
시뮬레이션을 하다 보면 형상의 변형이 클 때도 있는데, 이때 gaussian은 형상 표면에 위치하는 특성이 있기 때문에 형상이 깨지거나 렌더링 퀄리티가 떨어지는 문제가 있다. 이를 완화하기 위해서 형상의 내부에도 적절한 양의 gaussian을 임의로 채워넣어주는 방법이다.  1) opacity를 기준으로 형상 내부와 외부를 구분하는 것으로 시작하는데 일단 voxel 공간을 잡는다.  2) 그리고 grid cell 마다 상하 좌우로 ray를 쏜다. 3) ray를 따라 cell을 훑으면서 지나가는데 opacity가 낮은 값에서 큰값으로 변화하는 지점을 만나면 surface하고 판단한다. 4) 내부일 경우 상하좌우 모든 ray가 surface에 만날 것이므로 상하좌우 충돌 여부를 세서 내부인지 외부인지 분간한다. 5) 추가적으로 외부라고 확실시 되는 위치에서 현재 확인 중인 cell로 ray를 쐈을 때 짝수로 표면과 충돌하는지도 확인해준다.  condition 2 그림과 같이 외부에서 내부로 쏠 경우, 진입할 때와 탈출할 때 짝수 번 충돌할 것이기 때문이다.

추가적으로 3D gaussian이 특정 방향으로만 뾰족할 경우, 시뮬레이션으로 큰 변형이 가해졌을 때 튀어나와서 부자연스러운 결과를 만들 수 있다. 그래서 되도록 동글동글 3d gaussian이 되도록 각 방향으로의 scale 값이 특정 기준 r 이상으로 높아지지 않도록 억제하는 loss를 추가했다고 한다. 이건 학습 시 선택적인 것! 꼭 안해도 됨.