반응형
내 맘대로 Introduction

이 논문은 DreamFusion의 상위 호환(?) 정도 되는 논문으로 볼 수 있다. DreamFusion과 같은 시기에 제출된 논문이지만 DreamFusion이 arxiv에 올라온 이후에 제출된 논문이라 시간적으로는 DreamFusion 후속 연구에 가깝다. 후속 연구답게 목표로 하는 task는 text-to-3D이며 기존 2D diffusion model을 이용하여 3D로 어떻게 lifting하는지가 주 관심사다.
핵심 아이디어는 DreamFusion에서 소개한 SDS loss를 더 면밀히 파고들어 수학적으로 전개한 SJC(Score Jacobian Chaining) loss를 소개한다. 사실 SDS loss를 참고한 모양처럼 보이지만 별도로 연구했는데 공교롭게 먼저 나온 SDS loss가 SJC와 유사한 결론에 이르렀다고 말하는게 더 정확할지도 모르겠다.
하지만 확실히 DreamFusion보다 더 논리적으로 전개한 논문이기 때문에 가치있다고 생각한다. DreamFusion에서는 "발견해냈다"라고 설명한 부분들이 이 논문에서는 "도출되었다"라고 소개되기 때문에 개인적으로 더 믿음이 간다.
메모하며 읽기
   |
목적 자체는 2D diffusion model를 어떻게 3D 로 lifting하는지 그 방법을 구현하는 것이다. 그 방법에 있어서 핵심 질문은, 2d diffusion model이 뱉어주는 denoising 값을 gradient로 사용하고 chain rule을 이용해 3D asset에 해당하는 파라미터를 업데이트할 수 있지 않을까? 이다. 가능하다면 2d diffusion gradient + differentiable renderer gradient만 chain rule로 연결해서 때 3D asset 파라미터를 업데이트하면 된다. 이 논문은 그 수학적 전개를 다룬다. |
 |
diffusion model은 기본적으로 주어진 이미지가 gaussian distribution에서 생성된 이미지라는 가정하에 더 선명해지기 위해 필요한 denoise 량을 내뱉어주는 네트워크다. 수식(2)에서 eps(x)를 뱉어주는 역할이다. 이걸 해석해보면 이미지가 변화해야 되는 "변화량"을 의미하므로 다른 시선에서 보았을 때 하나의 gradient라고 볼 수 있다. diffusion model을 이용해 다른 네트워크의 파라미터를 업데이트할 수 있는 이론적 근거가 바로 eps(x)를 gradient로 바라보는 시선 때문이다. |
  |
여기서 diffusion model에서 이미지 x distribution을 전부 gaussian으로 가정했기 때문에 수학적으로 eps(x)와 실제 이미지 x distribution p(x)를 구체적으로 엮을 수 있게 된다. 수식(3)과 같은데, eps(x) / std 만 해주면 실제 p(x) 상에서 변화량을 알 수 있다. 직관적으로 말하면 이미지 변화량 갖고, 이미지 생성 distribution 상에서의 변화량까지 간단히 알 수 있게 되는 것이다. 육안으로 식별 가능한 이미지 변화 -> 육안으로 못보는 이미지 분포 변화 계산 가능. ---- 수식(3)의 LHS 값이 분포에서의 변화량이므로 의미가 크다. 따라서 이 개념을 score라고 정의한다. diffusion field에서. |
 |
수식(3)과 같이 정의했는데 사실 D(x)는 모르는 값이기 때문에 구현이 어렵다. 하지만 한 번 더 모든 diffusion model이 gaussian distribution을 따른다는 가정에서 출발했기 때문에 D(x)도 approximation해서 추정해낼 수 있다. p(x)가 gaussian 이라는 것을 알고 있으면 수식(5)와 같이 찾아낼 수 있다. ---- 논리적 점프가 많지만, 결론적으로 의미하는 바는 score 자체가 이미지랑 sigma만 잘 알고 있으면 다 계산할 수 있다는 점이다. |
 |
score p(x)를 수학적으로 전개하는 것까지 마쳐서 이미지랑 sigma만 있으면 계산해낼 수 있다는 것까지 보았다. 그 다음은 3d 로 lifting하는 과정이다. p(x)는 어디까지나 x가 이미지기 때문에 2차원을 다룬다. 이를 3차원 분포 p(θ)로 확장하기 위해선 하나의 가정이 필요한데 그게 수식(6)이다. 저자가 정의하길, 만약 3차원 asset을 생성해내는 distribution p(θ)이 있다면 그 분포를 여러 시점으로 projection했을 때 생성되는 p(x_projected)와 강하게 연결되어 있을 것이다. 따라서 projection된 값들 p(x_projected)를 전부 평균낸 결과가 p(θ)라고 정의했다. (말이 어렵다.) ----- 3차원 분포가 projected 2차원 분포들의 평균이라는 가정을 깔고 시작하면 2차원 수식 전개가 계속 이용 가능하기 때문에 수식(11)까지 이어진다. 수식(11)만 직관적으로 다시 보면 3D score는 2D score * projection Jacobian으로 계산할 수 있게 된다. 즉, 2차원에서 score 계산하고 differenctiable rendering 과정에서 발생하는 jacobian만 뒤에 곱해주면 3차원 score가 된다고 전개한 것이다. |
 |
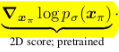 수식(11) 중 위 부분, 2차원 score 계산하는 부분을 먼저 본다. 단순히 diffusion model에 이미지 x를 던져주면 2D score가 나온다고 생각할 수 있지만 그렇지 않다. 원래 diffusion model의 입력은 noisy image다. 하지만 지금은 생성된 이미지 x를 넣기 때문에 noise가 없는 이미지에서 score를 계산해야 하므로 문제점이 있다. (OOD 문제) 네트워크가 한 번도 깨끗한 이미지를 본 적이 없기 때문에 깨끗한 이미지가 들어왔을 때 당황한다고 보는게 맞다. 직관적으로 보아도.. noise가 없는 이미지는 변화량이 0에 가까울 것이므로 score가 0 혹은 쓰레기값이 나올 것이라고 볼 수 있다. ----------- 따라서 이러한 문제를 풀기 위해서 깨끗한 이미지에 noise를 첨가해서 diffusion model에게 보여주어 score를 얻어내고, 이 score를 이용해 깨끗한 이미지일 때 score를 approximation하는 방법을 소개한다. 개똑똑하다. |
 |
간단하게 diffusion model이 깨끗한 이미지에선 오히려 실패한다는 것을 실험해보았는데, 이미지 가운데 주황색 원을 그린 이미지 x를 입력으로 diffusion model을 적용해보면 중간 이미지처럼 가운데 원 영역에 대해서 denoising을 제대로 못하는 것을 볼 수 있다. 반면 주황색 원 이미지에 noise를 salt and pepper처럼 임의로 주고 돌리면 세번째 이미지처럼 훨씬 잘 denosing 한다. --------- 이 결과로 하여금 네트워크가 깨끗한 이미지는 오히려 본적이 없어서 OOD 문제로 성능 문제를 겪는다는 것을 알 수 있다. |
  |
앞서 언급한 바와 같이 깨끗한 이미지에서 오히려 실패하므로, 일부러 noise를 주어서 score를 계산하고 깨끗한 이미지 버전 score를 approximation해내는 방법을 소개한다. (PAAS) 일단 noise를 부여할 때 이미지 분포 x가 원래 사용하는 sigma 만큼 씩 준다. 그러고 수식을 전개해보면 수식(16)과 같이 마지막 term 하나가 잘려나가므로, 실제로 이미지 x에 noise를 준 버전 n개 이미지 만들고 score를 평균 내기만 하면 된다는 것을 알 수 있다.  (직관적으로도 그냥 n번 noise augmentation하고 평균내면 되겠다 싶었는데 수식적으로도 그게 맞는 소리라는 것이다.) |
 |
수식(13)에 sqrt(2) sima 가 표기되어 있는 이유는 다음과 같다. 수식(16)과 같이 n개 noise 버전 score를 평균낸 것을 조금 더 계산해보면 sqrt(2)*sigma를 갖고 있는 이미지 분포에서 만들어낸 score와 같기 때문이다. (나도 이해못함. 근데 논리적 점프를 하고 넘어가는게 나을 듯) p_sqrt(2)sigma(x) = E[ p_sigma(x+sigma*n)] 이라 같은 것이다. score 계산을 위해 양 변에 log를 씌우고 jensens' inequality 를 적용하면 수식(18)과 같이 정리할 수 있다. --- 이건 어디에 쓰겠다가 아니라 그냥 전개해보니 수학적으로 이런저런 맞아 떨어지는게 있다고 기반을 보여주는 것. |
 |
결론적으로 깨끗한 이미지가 들어오면 sigma만큼 noise 주고 n번 score 계산하고 평균내서 사용하면 깨끗한 이미지 score다. |
 |
이제 드디어 jacobian 쪽이다. 이건 진짜 간단하다. rendering 과정은 딱 정해진 함수대로 이루어지기 때문에 jacobian이 명확히 계산될 수 있다. 직접 구현할 필요도 없고 그냥 differentiable renderer 가 pytorch로 구현되어 있으니 backpropagation을 call해주면 자동으로 얻을 수 있다. ---- 나머지 내용은 NeRF를 구현할 때 TensoRF와 같이 voxel representation을 사용했다는 점과 ray point sampling이 복잡하니 정해진 d 간격를 사용해 sampling했다는 디테일을 길게 설명하는 것이다. |
 |
diffusion model이 좋다고는 하지만 여전히 3D GT를 제공해줄만큼 정확하진 않으므로 불안불안하게 학습된다. 따라서 NeRF의 고질적인 문제 현상인 cloud noise가 잦은데 이를 제거하기 위해서 alpha-composited weight 자체가 0에 가깝도록 regularization을 걸어주었다고 한다. |
 |
weight를 0으로 잡아당기는 행위를 처음부터하면 당연히 망가질 것이기 때문에 K iteration을 기준으로 lambda값을 조정하는 스케쥴링도 적용해주었다. |
 |
|
  |
이건 되게 부수적인 것 같은데, 실제로 학습을 시켜보니 3D asset이 정중앙에 안 있고 이리저리 날라가있는 현상이 있었다고 한다. 따라서 미리 이미지 bbox를 따놓고 bbox 내부는 depth가 가깝게, 외부는 멀게 하는 식으로 조절해주었다고 한다. |
 |
마지막은 arxiv에 미리 올라와있던 DreamFusion과 비슷한 점이 논문 제출 당시 마음에 걸렸는지 대놓고 DreamFusion과의 차이점을 적었다. 요약하자면 DreamFusion은 실험하다가 "발견해냈다"라고 한 점이 우리가 "도출해낸" 점과 유사하다고 지적했다. 그래서 더 이론적으로 탄탄하다고. 그리고 PAAS같은 기법이 2D diffusion score를 더 효과적으로 쓸 수 있게 함으로 novelty가 있다고 설명한다. 마지막에 소심하게 DreamFusion을 참고하긴 했다고 적는게 정직해보이기도 한다. |
 |
sigma값을 선별할 때 random으로 할지 annealing하면서 점점 작게 쓰는게 좋을지 비교 실험한 결과. |
 |
  |
반응형
