반응형
내 맘대로 Introduction

이 논문은 한마디로 Instant NGP의 SDF 버전 논문이다. Instant NGP는 view synthesis용으로 NeRF 첫 논문의 초 가속화 버전 논문이었는데 이를 3D reconstruction에 특화된 NeRF로 확장하는 논문이다. 핵심적인 내용은 hash encoding 기법을 2nd order derivate 계산에 적용한 것이다. 모든 3D surface reconstruction NeRF들이 속도 문제로 고생할 때 벽처럼 다가오는 것이 2nd order derivate 계산이 기능적으로 지원되지 않았던 점이다. surface reconstruction에 코어인 normal과 eikonal loss를 사용할 수 없기 때문이다. hash encoding 기법으로 2nd order derivate도 커버할 수 있도록 수정하여 속도와 성능을 둘 다 잡는 논문이라고 할 수 있겠다.
메모하며 읽기
  |
(Preliminaries section은 NeRF와 NeuS, Instant NGP 내용의 한 문단 요약들이므로 생략한다.) 먼저 SDF 개념을 사용하면 eikonal equation을 비롯해서 2nd order derivate가 등장하여, double backward operation이 필요하다. 하지만 이는 기능적으로 지원되지 않을 뿐더러, voxel grid를 사용하기 때문에 아래와 같이 trilinear interpolation도 포함해야 하는데 round function이 non-differentiable인 문제도 있다. rounding operation은 수식(7)과 같이 풀 수는 있다고 해도 문제는 남아있다. |
  |
그리고 (잘은 모르겠지만) hash encoding을 사용하게 되면 trilinear interpolation을 하더라도 local grid cell에만 제한된다. (구조 상 옆 voxel grid와도 맞아떨어지도록 interpolation하기 어렵고 지금 대상으로 보고 있는 voxel에서만 interpolation된다는 뜻 같다.) 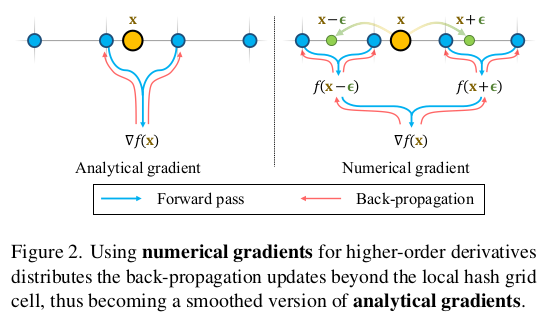 그래서 이를 해결하고자, 특정 step size epsilon을 정의하고 이것을 이용해서 numerical gradient를 만들었다. 옆 voxel의 analytical 값들을 interpolation해서 현 voxel 값을 강제로 만드는 것이다. 일반적인 volume trilinear interpolation하면 이게 당연한 소리 같지만 hash encoding에서는 이게 안통하는 개념인가보다 강제로 locality를 넘어서서 trilinear interpolation 효과를 만들고 gradient를 수식(8)과 같이 만들어서 썼다. |
  |
numerical gradients를 사용하게 되면서 step size라는 파라미터가 생겼고 필연적으로 coarse-to-fine으로 학습하는 방식을 사용하게 되었다. step size가 클 땐 global하게, step size가 작을 땐 local하게 interpolation이 될테니 말이다. 또한 hash grid 구조 상 여러 level이 존재하는데 step size에 맞추어 level을 나누어 순차적으로 학습되게 함으로써 효율을 확보할 수도 있다고 한다. |
 |
loss는 기존 논문들과 완전 동일하게 color loss, eikonal loss가 주축이다. 독특하게도 curvature loss라고 SDF의 2차 미분 값을 0으로 보내는 loss를 설계했다. (그럼 backward는 triple backward인데... 직접 구현한 것 같다.) |
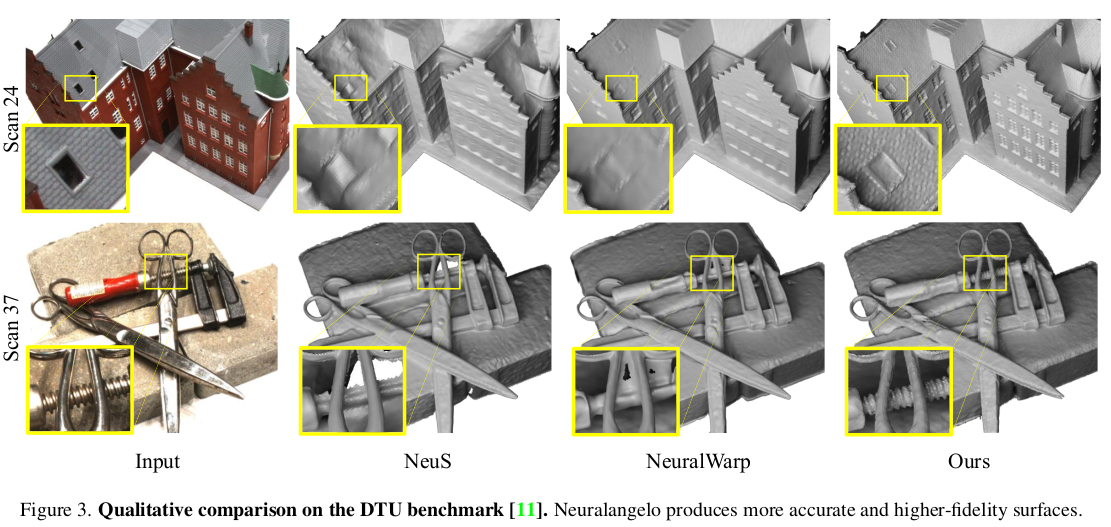 |
 |
 |
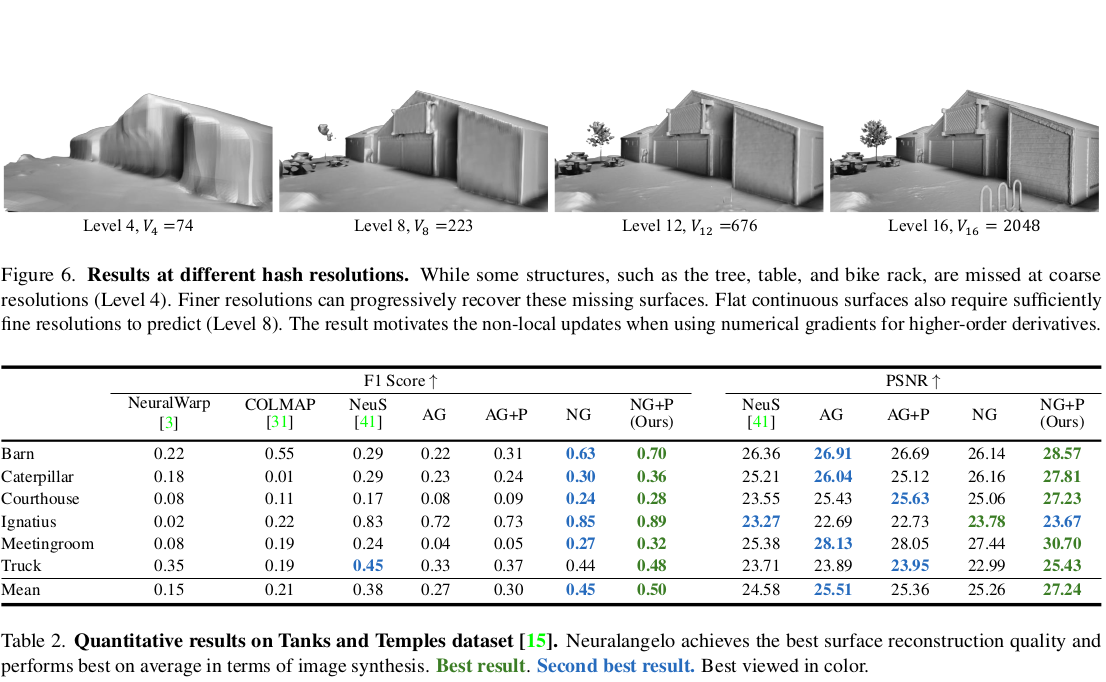 |
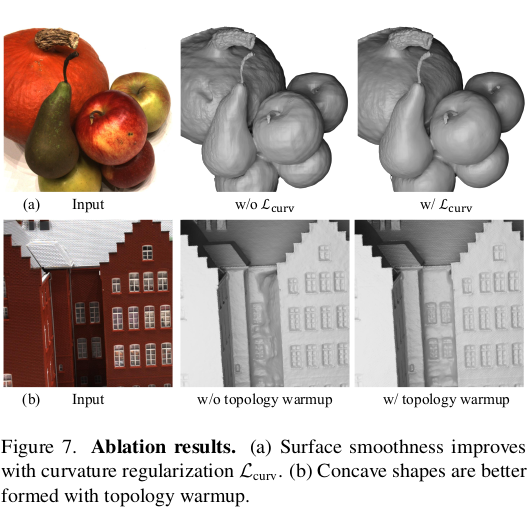 |
 AG : analytic gradient NG : numerical gradient training이 약 25% , inference가 50~60% 정도 빠르다 |
반응형
'Paper > 3D vision' 카테고리의 다른 글
| FreeNeRF: Improving Few-shot Neural Rendering with Free Frequency Regularization (0) | 2023.07.06 |
|---|---|
| HF-NeuS: Improved Surface Reconstruction Using High-Frequency Details (0) | 2023.07.06 |
| Light Field Neural Rendering (0) | 2023.06.30 |
| RoMa : Revisiting Robust Losses for Dense Feature Matching (1) | 2023.06.29 |
| PET-NeuS: Positional Encoding Tri-Planes for Neural Surfaces (0) | 2023.06.29 |