반응형
내 맘대로 Introduction
DKM (이전 글) 저자의 후속 연구로 나온 dense feature matching 네트워크다. 목적은 DKM와 같고 입력 출력의 형태도 같다. DKM 상위호환으로 보는 것이 맞을 것 같다. DKM이 GP regression을 사용해서 matching 성능을 끌어올린 것과 같이 RoMa도 다소 어려운 수학 개념을 녹여서 성능을 끌어올렸다. Diffusion 논문 때문에 그나마 조금 익숙한 Markov chain을 가져왔다.

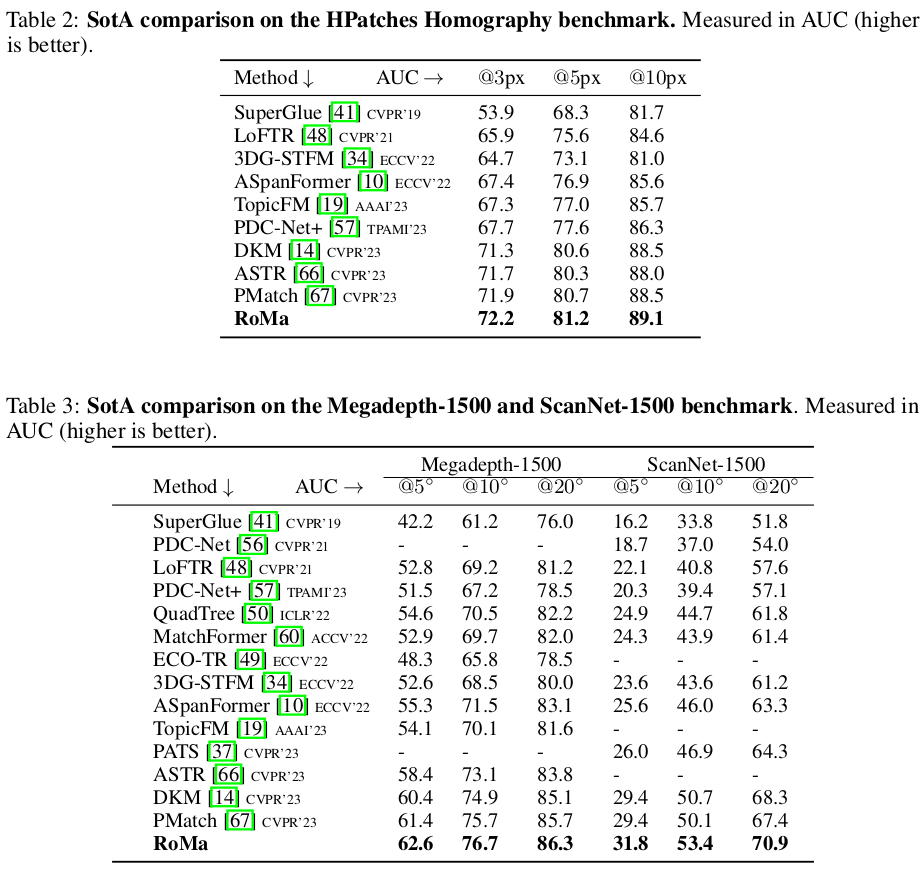
backbone을 DinoV2와 같이 어마어마한 것을 사용했기 때문에 성능이 뛰어오른 것인지 저자가 제안한 새로운 개념 때문에 뛰어오른 것인지 정확히 분간은 안가지만 성능을 DKM 대비 더 좋다. 속도는 당연히 느린데 측정해보니 대략 4배 정도 느린 것 같다.
메모하며 읽기
   |
|
| 그림만 봐도 어마어마하게 복잡해보인다. 전체 컨셉은 matching 문제를 diffusion process로 바라보고 풀겠다는 것이다. 직관적으로 이해해보자면 대충 matching -> 보다 정확한 matching -> 정확한 matching 처럼 coarse-to-fine으로 나아가는 컨셉이 일반적인 matching network의 구조인데 다른 관점에서 보면 diffusion process랑 닮아있다는 점에서 착안한 것이다. 더욱이 coarse 와 fine은 단순히 scale만 다르다고 생각할 것이 아니라 해야하는 역할과 집중해야 하는 부분이 다르다고 말하며 각각 stage을 분리했다고 한다. 대략 coarse stage는 대충 큰 그림에서 영역 수준의 matching에 집중을 해야하고 fine stage는 coarse stage가 맺어준 영역 내에서 정확하게 한 곳으로 수렴하는데 집중해야한다고 말한다. |
  |
| 앞서 언급한 바와 같이 matching을 coarse -> fine으로 나아가는 과정을 diffusion process처럼 바라보는 논문이기 때문에 markov chain을 가정한다. DKM을 읽었다면 알겠지만 feature matching을 conditional probability로 보는데 markov chain을 가정하는 것을 더하면 finest level에서의 matching은 coarse -> fine 까지 모든 probability의 곱으로 표현된다. 수식(1)로 보면, 가장 해상도가 낮은 N level 에서는 대충 image to N level - conditional probability를 초기화한다. (코드를 보니까 GP regression을 썼다.) 그리고 그 다음 N to N-1 level conditional probability를 곱해줌으로써 (markov chain이니까) image to N-1 level conditional probability를 반복해서 만드는 식이다. |
 |
| 이론 전개는 쉬웠는데 이 이론으로 학습을 시키려면 이 의미와 맞는 loss 설계가 필요한데 이게 어려웠다고 한다. 그래서 diffusion 모델 논문에서 쓰는 variational lower bound 방식을 가져왔다고 한다. p는 위에서 다룬 그대로 coarse to fine 방향으로 가는 p()이고, q는 그 반대인 fine to coarse로 나아가는 방향인데 이게 또 정의하기가 어렵다. 왜냐면 일반 diffusion이었다면 그냥 noise를 더하면 되겠지만, matching을 noisy하게 만드는건 어떻게 하는게 맞는 걸까? 위치를 그냥 위아래로 흔들면 되나? 그게 효과적인게 맞는지 denoising이 쉽도록 하는게 맞는지 검증이 안됐다. |
 |
| q를 그래서 어떻게 만들었냐. scale-space theory에서 영감을 얻었다는데 무슨 영감인지는 잘 모르겠고, gaussian kernel (size를 s로 조절하는)을 씌워서 fine to coarse를 구현했다. 왜인지 설명을 들어보면, 한 point, x가 coarse level에서 matching이 되었다고 치자 근데 이미지가 반복되는 패턴이 많았다면 이 matching이 잘못되었을 확률이 높다. 다른 위치에 matching 돼야 했을 수도 있으니까. 그래서 matching을 할 때 multimodal로 여러개 매칭을 고려할 수 있도록 multimodality를 부여하고 싶었다고 한다.  그림으로 보면, 만약 matching이 1대1로만 된다면 맨 왼쪽처럼 선 하나로만 그려질 것이다. 어느 xA를 보아도 1대1 매칭이 된다. 그리고 foward, q 가 그냥 bilinear downsampling이었다고 해보자. 그럼 q(xB | xA) 를 생각해보면 한 위치에서만 impulse function처럼 튀어나온 모양이 될 것이다. 그렇다면 여러 위치에 matching 가능성을 표현할 능력이 없을 뿐더러 backward, p function이 impulse function에 대응해야 하니 효율이 떨어진다. 근데 forward, q가 backward, p에 gaussian kernel을 씌워진 형태였었다고 해버리면, 상하좌우 매칭 가능성을 열어버리는 것이 되어서 노란 점선 위치의 xA는 smoothing의 효과로 두가지 matching 가능성을 갖게 된다. q(xB |xA)로 보면 두 위치에서 impulse보단 덜 뾰족한 형태로 확률이 그려진다는 것을 볼 수 있다. 최종적으로는 1대1 매칭이 나와야하는 것은 맞다. 그렇지만 추론 단계에서 가능성을 열어준다음 최종적으로 1개로 수렴하도록 하는 것과 가능성이 없는 상태에서 1개로 수렴하는 것은 성능 차이가 크다는 입장이다. |
  |
| (정확한 이해인지는 자신이 없다.) 앞서 설명한 것과 같이 forward, q를 설계하고 관찰해보니 gaussian kernel 사이즈에 따라 q(xB|xA)의 모양이 많이 달라지는데 search space를 넓히면 (kernel을 키우면) 너무 모양이 넙적해지므로 확률값들이 전반적으로 낮아지는 경향이 있고, search space를 좁히면 (kernel을 좁히면) 모양이 뾰족해지므로 확률값은 높아지만 multimodality는 줄어든다. search space를 넓힘과 동시에 신뢰도 높은 특정값을 한 번에 찾는 것을 어렵다는 결론이다. 따라서 coarse와 fine level에서 가져가야하는 목적성이 다르고, coarse level에서는 search space를 넓혀 mulmodality를 넓히는 것, 다른 말로 global consistency를 강황하는 것에 집중해야 하며 fine level에서는 search space를 좁히면서 단 하나의 값으로 확률을 높이며 수렴하는 것에 집중해야 한다. coarse level에서 큰 그림을 보며 global consistency, multimodality를 확보하기 위해선 수식 (6)과 같은 loss로 학습을 해야 하고 fine level에서는 전혀 다른 loss로 학습을 해야한다고 소개한다. loss에 대한 자세한 설명은 다른 section에 나와있다. |
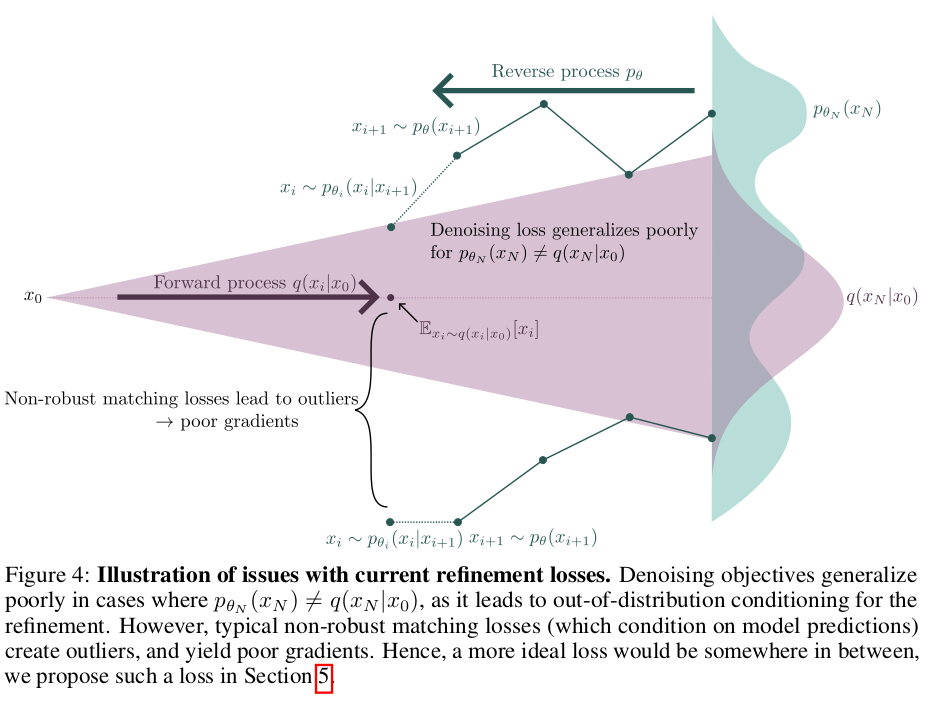 |
| fine level에서 사용하는 loss는 위와 같이 정의했지만 하나 짚고 가야하는게 더 있다. 수식(10)을 제안하긴 했지만 분석을 해보니 loss에 아쉬운 부분이 있었다고 한다. p(xN) 과 q(xN|x0)가 같지 않을 때, 즉 일부 이미지 feature들은 위와 같이 p와 q를 설계하는 것이 안 맞아 떨어질 때 성능이 떨어진다고 한다. 그렇다고 해서 일반적으로 많이 쓰는 Non-robust matching loss를 쓰면 가끔 튀는 값에 대응이 안돼서 학습이 불안해진다고 한다. (그림의 하단부 수식을 보면 수식(10)꽈 달리 뒤에 x_i+1 이전 예측값이 붙어있는 것을 볼 수 있는데 이전 예측값이 쓰레기이면 연쇄적으로 다 튀어나가는 구조의 loss 이므로 학습이 어렵다는 뜻 같다.) |
  |
| 다시 요점 정리하면, coarse와 fine을 반드시 decouple되어야 하며 각각에 사용되는 loss도 달라야한다는 주장이다. |
  |
| coarse용 네트워크와 fine용 네트워크가 분리되어 있다. coarse encoder는 무려 DinoV2, decoder는 position encoding을 뺀 ViT를 사용했다. fine을 진행할 때는 VGG와 ResNet feature를 고민하다가 VGG feature가 더 localizable 특징이 더 강해서 VGG feature를 끌어와서 추가로 넣어준다. 나머지 fine decoder는 DKM이랑 똑같은 엄청 얇은 CNN이다. 코드 보면 똑같이 coarse encoder에서 나온 feature 중 fine feature에 해당하는 부분이 skip connection으로 넘어오는 듯 하다. |
 |
| coarse loss 는 앞선 variational lower bound 수식에서 앞부분에 해당하는 영역만 따와서 loss로 사용하며 쉬운 전개를 위해 위와 같이 정의해서 사용했다. 수학적 의의보다는 loss term의 간소화를 위해 이렇게 정의한 것이 더 큰 것 같다. 수식 (13)과 같아지니 말이다. |
  |
| 앞서 제안한 refinement loss는 아쉬운 점이 있다고 했다. 그래서 Non-robust loss를 쓰면 또 다른 outlier 문제가 있고. 그래서 한 스텝 더 나아가서 generalized robust loss를 찾아서 썼다고 한다. 차이를 직관적으로 표현해보면 Non-robust loss에서 outlier로 인해 튀는 경우가 생기면 interpolation으로 중간값을 사용하게 하는 느낌이다. |
 |
| 길고 길었지만 정리하면 수식(19)와 수식(20)을 각각 만들고 coarse와 fine에 나누어서 각각 학습에 사용하면 된다. 직접 코드를 보는 것을 추천. |
 |
 |
 |
 |
반응형