반응형
내 맘대로 Introduction

NeuS를 보완해서 High frequency 영역 성능을 끌어올리는 것을 목표로 하는 논문이다. 세가지 보완점을 말하는데 첫번째는 SDF to volume density 수식의 수정, 두번째는 low frequency와 high frequency의 분리 학습, 세번째는 SDF to transparency 조절을 위한 파라미터 추가이다. NeuS 핵심 수식을 가져와 사용만 하는 다른 논문들과 달리, 핵심 수식을 수정하는 것이 주요 내용이기 때문에 기본적으로 관심이 조금 간다.

참고로 두번째 보완점은 뜬금없이 등장한 것은 아니고 NeuS를 관찰해보니 low frequency는 잘 배우는데 high frequency는 못 배우는 경향이 있어 등장한 것이다.
메모하며 읽기
  |
| 3가지 보완점을 순차적으로 짚으면서 설명을 이어간다. |
 |
| SDF to volume density 과정을 모델링한 논문들을 살펴 보면, SDF to volume density로 바로 가는 VOLSDF 같은 류가 있고, SDF to weight to volume density로 한단계 거쳐 가는 NeuS 같은 류가 있다. 성능 측면에서 NeuS가 압도적이었기 때문에 후자를 정설로 여기면서 사용해왔었다. |
  |
| 이 논문에서는 SDF to volume density의 다음 스텝으로 이어지는 volume density to transparency에 주목한다. 즉, SDF to transparency까지 한 번에 바로 가는 것이다. 비약적 점프 같아 보일 수 있지만 수식을 전개해보면 오히려 장점이 뚜렷하다고 한다. transparency 미분 형태가 transparency 자체에 negative weighted가 걸리는 형태라는 것에 주목한다. transparency는 surface를 만나면 최대값이 된다는 것을 알기 때문에 2차미분 임계점 중 extremum을 찾으면 되는데 위와 같이 형태가 자기 자신이 들어있는 형태면 gradient 계산이 아주 쉽고 구현도 쉽기 때문이다. sdf 나 transparency나 monotonic function임이 동일하기 때문에 Ψ 함수를 정의하는 것도 쉽다. 단순 logistic sigmoid로 정의하고 slope를 조절할 수만 있도록 scale parameter를 추가하기로 했다. |
 |
transparency에서 역으로 weight와 volume density를 계산하는 것도 쉽다. 그냥 수식에 따라 역전개만 하면 되기 때문이다. 위와 같이 그냥 구현해서 쓰면 된다.  수식에서 출발한 단순한 발상치고 효과가 컸다고 한다. |
 |
| low to high frequency training을 위해 low용 네트워크와 high용 네트워크를 분리했다. low용 네트워크는 큰 형상을 high용 네트워크는 디테일한 형상을 잡는 용이다. 학습을 아예 따로따로 하는 것은 아니고 한 번에 학습하는데 수식 (10)과 같이 학습 시 point, x를 던져줄 때 그냥 던져주는 것이 아니라 high frequency 네트워크에서 추정한 양만큼 빼서 애초에 smoothing된 point를 던져준다. 그리곤 분리되어 잘 학습되길 기대하는 것이다. 하나 발견한 것은 high용 네트워크를 그냥 붙여주면 학습이 불안정하여 4* Ψ (f_b) 를 곱해주어 surfcae 근처인 것 같을 땐 강하게, 먼 것 같을 땐 약하게 하도록 가이드 해주었다. |
  |
| 추가로 low용 네트워크와 high용 네트워크에 걸어주는 positional encoding을 각각 다르게 했다. 컨셉과 맞아떨어지도록 low용 네트워크일 때는 low frequency로, high 용 네트워크일 때는 high frequency로 encoding했다. 더 나아가 학습이 진행됨이 따라 점점 더 freuquency가 커지도록하는 방식도 추가했다. (이건 박근홍 씨 논문에서 제안된 것이다. HyperNeRF였나 아무튼) 이후 학습은 NeuS, VOLSDF와 같이 color loss와 eikonal loss로 학습한다. 다만 low/high용 두 개이므로 eikonal loss가 base만 한 번 base+displace 한 번 총 두 번 들어간다. |
 |
| SDF to transparency를 수식(6)과 같이 쓰려다가 관찰해보니, high frequency detail을 잡으려고 노력하다보니 eikonal equation이 깨질 때가 빈번한데 eikonal loss로 학습하다보니 효과가 줄어들어 eikonal equation이 깨질 때 오히려 loss가 방해가 되는 일을 없애기 위해 약간의 수정을 했다고 한다. 그냥 기존 수식의 계수에 norm of gradient의 크기를 보고 1보다 크면 implicit function 변화가 크도록 기울기를 가파르게, 1보다 작으면 implicit function 변화가 작도록 기울기를 완만하게 바꾸는 값을 곱해주었다. |
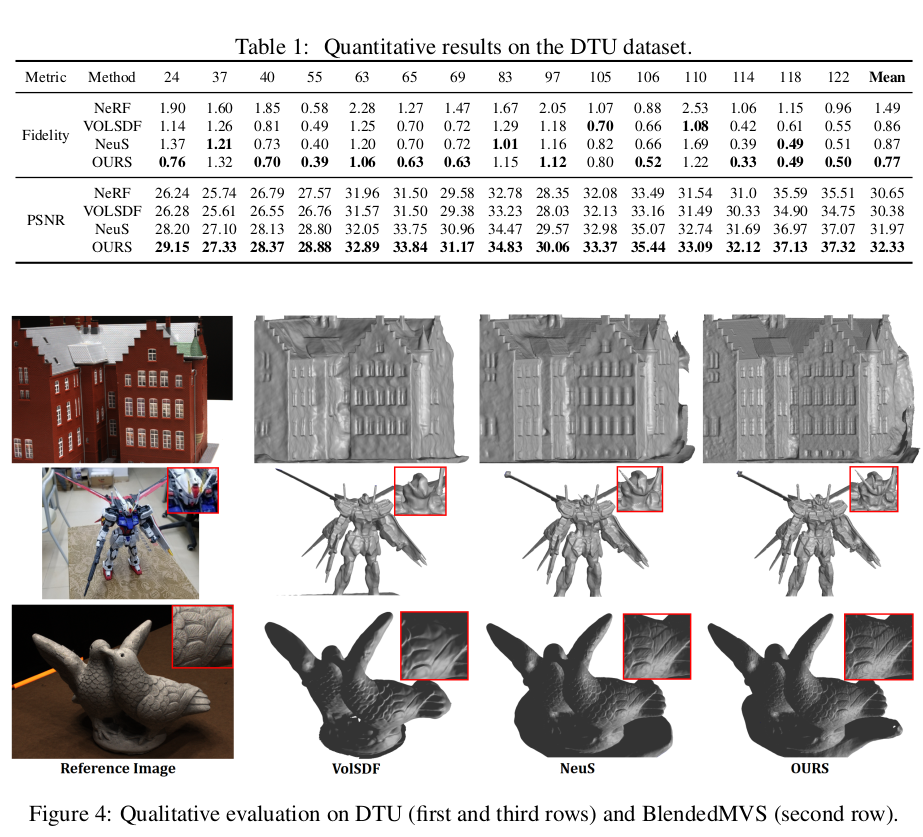 |
 |
 |
반응형
'Paper > 3D vision' 카테고리의 다른 글
| Generalizable Patch-Based Neural Rendering (0) | 2023.07.07 |
|---|---|
| FreeNeRF: Improving Few-shot Neural Rendering with Free Frequency Regularization (0) | 2023.07.06 |
| Neuralangelo: High-Fidelity Neural Surface Reconstruction (0) | 2023.07.03 |
| Light Field Neural Rendering (0) | 2023.06.30 |
| RoMa : Revisiting Robust Losses for Dense Feature Matching (1) | 2023.06.29 |