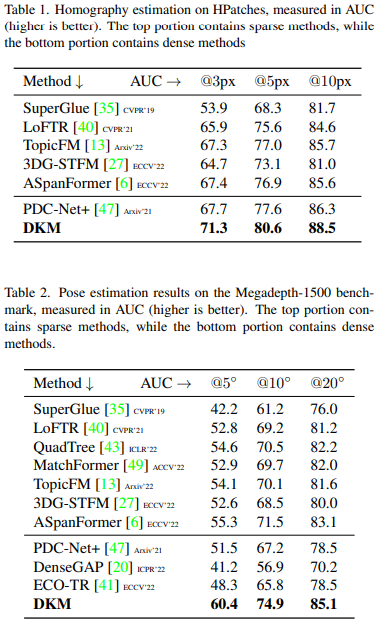
DKM: Dense Kernelized Feature Matching for Geometry Estimation

내 맘대로 Introduction
DKM 은 간단히 말해 feature matching 네트워크다. 즉, 두 이미지 간의 correspondence를 찾는 문제를 다루고 있다. SIFT나 SURF, ORB 등을 이용한 feature matching을 흔히 접해보았을 것이기 때문에 문제 자체는 익숙하다.
DKM만의 차별점은, sparse correspondence가 아니라 dense correspondence라는 것이다. SIFT를 예로 들면, 두 이미지에서 각각 feature point들을 뽑아내고 feature descriptor를 비교하여 matching하는 방식이므로 point 레벨에서 matcihng이 이루어진다. 하지만 DKM은 두 이미지 간의 모든 픽셀에서 matching을 시도한다. 흡사 optical flow에 가까운 feature matching인 셈이다.
주요 특징점은 dense correspondence를 찾는 것을 목적으로 하면서, descriptor가 효율적이지 않다고 생각했는지 feature descriptor가 명시적을 존재하지 않는 형태로 디자인했고 늘어난 matching 수를 감당하기 위해 certainty 추정을 포함하도록 디자인했다.
핵심 내용

전체 흐름은 크게 5단계로 나누어져있다. 하지만 끝의 4단계와 5단계는 기존 sparse correspondence 기반 3D geometry 알고리즘이 많다보니 이에 맞도록 output을 변경하기 위해 추가한 단계로 알고리즘적 의미는 크지 않다고 볼 수 있다. 따라서 크게 3단계 (feature extraction - global matcher - warp refinement)로 나누어졌다고 볼 수 있다.
feature extraction은 말그대로 입력 이미지에서 feature를 뽑아내는 역할을 담당하고, global matcher는 대략적인 matching 초기화, warp reifnement는 세밀한 matching으로 업데이트를 담당한다. 최종 출력은 이미지 A의 pixel이 이미지 B의 어느 pixel에 대응되는지 pixel offset (optical flow 포맷과 동일)과 해당 결과의 신뢰도, certainty로 나온다.
1. Feature extraction

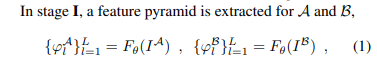
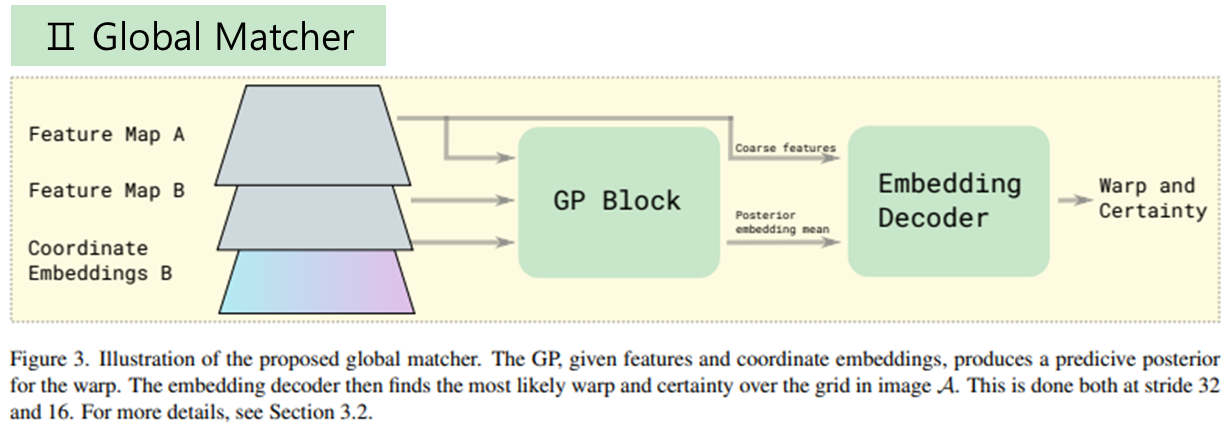
첫번째 단계인 feature extraction은 아주 간단하다. ResNet50을 backbone으로 사용한 Encoder가 전부이며 [32, 16, 4, 2, 1] 총 5레벨 해상도로 압축된 feature를 생성한다. 5레벨 중 [32, 16] 레벨은 coarse feature, [4, 2, 1] 레벨은 fine feature로 불리며 뒤에 각각 다르게 활용된다.
2. Global Matcher
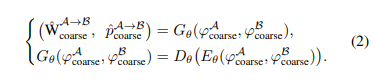
두번째 단계인 Global Matcher는 조금 복잡하다. 사실 복잡하다기 보다 dense matching 초기값을 계산하는데 그냥 단순히 앞서 나온 feature들의 유사도(similarity + argmin)를 계산하여 초기화하는 것이 아니라 GP (Gaussian process) regression을 이용하기 때문에 생소하다. 이미지 A의 픽셀이 이미지 B의 어떤 픽셀에 대응되는지 찾아내는 문제는 regression 문제로 간주할 수 있기 때문에 단순한 matching보다 regression method를 이용하는 편이 더 정확성을 높일 것이라고 기대한 듯하다.
GP regression으로 초기값을 계산한 뒤, coarse feature와 함께 decoder를 통과시켜 coarse matching 결과를 얻어낸다.
여기서 잠시 GP regression이 무엇인지 아주 아주 초간단 요약을 하면 다음과 같다.

* Random process의 정의는 Random variable의 무한차원 확장판이다. 직관적으로 이해를 해보자면 시간에 따라 달라지는 확률 분포를 상상하면 편하다. 시간이 확정되면 그제서야 확률 분포가 확정되고 우리가 아는 Random variable이 될 것이다. 그렇다면 만약 더 나아가 차원이 1개(시간)만 늘어난 것이 아니라 여러개가 추가되면 어떨까? 가령 시간과 장소 차원이 추가되거나, 기타 차원이 추가될 수도 있고 무한개의 차원이 추가될 수도 있다. 이 경우를 모두 포함하여 random process라고 부른다. 사실 상 random variable의 함수 버전이다.
* Gaussian process는 Random process 중 어떤 차원이 결정돼도 확률 분포가 Gaussian으로 확정되는 random process를 말한다. 가령, 시간에 따라 변하는 확률 분포가 있을 때 어떤 시간에 보아도 mean, std는 다르지만 gaussian이 되는 경우를 말한다.
GP regression은 Gaussian process, f(x)가 있다고 가정하고 시작한다. 즉, n차원의 값, x에 따라 확률 분포가 확정되는 상황으로 x가 결정되면 튀어나오는 f(x)들은 mean, std는 다르지만 gaussian인 상황인 것이다.
GP regression이 하고자 하는 것은 정해진 n차원 값, x 그리고 이에 따라 확정되는 분포 f(x) 여러 개를 갖고 새로운 x*가 들어왔을 때 나올 분포 f(x*)를 예측하는 것이다.
시간으로 비유해서 설명하면, 1초부터 10초까지 초마다 확정되는 확률 분포 10개를 보고 11초 때 확정될 확률 분포를 예측하는 것이다.
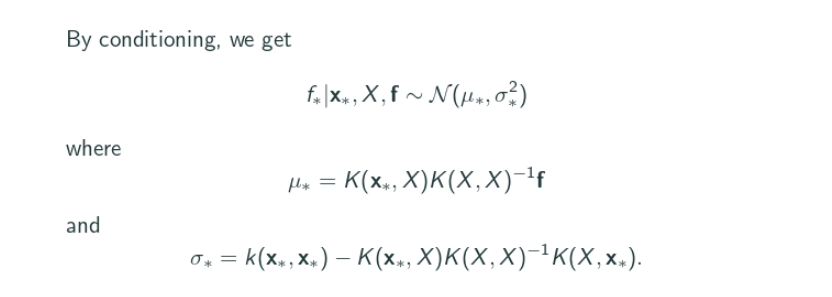
전개 과정을 생략하고 수학적으로 조금 점프를 한 뒤 결론부터 말하면, 위와 같이 갖고 있는 x <-> f(x) 쌍, X<-> f 를 갖고 mean* 와 std*를 계산하면 되는데 이 mean*와 std*가 새로운 x*가 주어졌을 때 확정될 확률 분포의 mean과 std다.
다시 시간으로 비유하면 1초부터 10초까지의 x <-> f(x)를 갖고 위 수식으로 mean*와 std*를 계산하면 이게 11초 때 확정될 확률 분포의 mean과 std다.
실제 이를 활용하고자 할 때 확률 분포 f(x)를 알고 있을 수는 사실 없고 f(x)에서 직접 "관찰"된 observation, y를 알고 있을 수 밖에 없으니 실제로는 다음와 같이 계산한다.

관찰값 y에 오차를 임의로 부여해서 f(x)를 모사한다.

이해를 더 돕기 위해 그림 예시를 들면, 왼쪽 그림처럼 x와 observation, y를 잔뜩 알고 있고 x*가 새로 들어왔을 때 어디(y*)에 찍힐지 찾아보면 GP regression으로 분석한 결과, y*~f(x*)는 우측 그림과 같이 mean* (진한 파랑선)와 std*(회색 범위) 안에 찍힐 것으로 예상된다. GP regression으로 찾으면 certainty(std*)도 나오는 것이 장점이다.
다시 DKM을 돌아와 이를 어떻게 활용했는지를 보자.
GP regression term에 일대일 대응을 시켜보면 이미지 B의 feature들이 N차원 값 x 이고 이미지 B의 coordinate가 f(x) (정확히는 f(x)의 관찰값 y)다.
coordinate가 확률 분포인데다가 gaussian 이라는 것이 이해가 안될 수 있는데 그냥 그렇게 정의한 것이다. coordinate 값은 확률로 보기에 값의 범위도 그렇고 의미도 그렇고 안 맞을 수 있는데 positional encoding으로 값 범위를 대충 맞춘 뒤 확률 분포에서 나온 observation이라고 정의함으로써 GP regression 프레임워크에 우겨넣은 것이다.
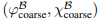
이를 이용해 GP regressor를 설계하면, 알고 있는 이미지 B feature <-> 이미지 B의 coordinate 쌍들로 학습한 것이고 결과적으로 새로운 이미지 B feature, x*가 주어졌을 때 이에 대응될 이미지 B의 coordinate가 gaussian 분포 형태로 나오게 된다.

DKM은 이렇게 GP regressor를 설계해두고 나서, 이미지 B가 아닌 이미지 A에서 뽑은 feature를 x*로 사용하는 트릭을 구사한다. 그러면 GP regressor는 "이미지 A feature, x*에 대응되는 이미지 B의 coordinate 분포를 예측하게 된다"!
이미지 feature는 이미지 A든 B든 동일하게 뽑혔을테니 타당한 트릭이다.

이해를 돕기 위해 그림으로 보면 위와 같다.
결과를 해석해보면 이미지 A의 특정 픽셀이 이미지 B의 어느 픽셀에 대응될지 "확률적"으로 알아낼 수 있게 된다.
DKM은 이 결과를 Global matcher의 초기값으로 활용했으며 간단하게 mean*만 사용하고 std*는 버렸다.

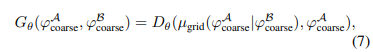
이제 그림이 이해가 될텐데 위 그림의 posterior embedding mean이 mean*이다.
3. Warp refiner

마지막 핵심 단계는 refinement다. coarse feature를 이용해서 초기 추정을 수행했으니 이제 fine feature로 이를 섬세하게 다듬는 단계다. 이 부분은 [8, 4, 2, 1] 레벨의 feature들이 사용된다.
Warping module은 현재 갖고 있는 warp, certainty 값으로 이미지 B의 feature를 A와 pixel aligned 형태로 재구성한다. 그리고 이를 이미지 A feature 뒤에 concatenation하는 기능을 수행한다.
Warping embedding은 현재 갖고 있는 warp, certainty 값을 upsampling해서 해상도를 맞춰주는 기능을 수행한다.
Warping module과 warping embedding은 뒤이은 refiner block을 통과하고 warp, certainty residual을 계산한다.
이 과정은 [8, 4, 2, 1] 총 4번 반복된다.
5. Loss

Loss는 비교적 간단하다. warp 값은 optical flow 처럼 dense pixel correspondence GT를 직접 사용해서 supervision을 제공하고 certainty 역시 dense certainty GT를 직접 사용해서 supervision을 제공한다.
certinaty GT는 생성한 것인데 기존 데이터셋에서 제공되는 depth GT와 correspodence GT로 찾은 depth의 차이가 적을 경우 1로 점수화해서 생성했다고 한다.
Result
압도적인 성능과 더불어 압도적인 generalization 성능을 보여준다!