반응형
내 맘대로 Introduction

반사가 심한 물체 표면을 어떻게 복원할 것인가에 대한 논문이다. 반사가 일어날 경우, 기존 알고리즘에서 가정하는 volume rendering 수식을 안통하기 때문에 모델링 결과가 처참한데 반사광을 따로 다루어 복원 성능을 끌어올린 논문이다. 세팅이 복잡해서 직접 사용해볼 엄두는 나지 않는 논문이다.
이 논문 역시 NeuS를 baseline으로 잡고 있는데 NeuS 수식을 그대로 이용하되 color network를 단순히 MLP 붙이고 끝이 아니라 BRDF 수식을 이용해 추가적인 모델링을 한 MLP를 사용한다.
메모하며 읽기
  |
2 stage로 구성되어 있는데, 대충 coarse to fine 컨셉이다. 첫번째 스테이지에서 SDF + BRDF를 잘 녹여서 거의 90% 만들어두고, 두번째 스테이지에서는 첫번째 스테이지에서 사용한 approximation을 보완하기 위한 작업을 하며 나머지 10%를 만드는 느낌이다. 기본 baseline은 NeuS다. |
 |
NeuS를 배경지식으로 설명하는데, 여기 적혀있는 내용은 volume rendering 내용이지 NeuS의 핵심 내용은 아니다. NeuS를 읽고 와라 정도의 내용. |
  |
1982년 논문... 대략 내용은 빛은 diffuse와 specular가 합쳐져서 특정 색깔을 발하게 되는데 그 각각을 수식으로 모델링한 논문이다. 수식(3)과 같이 적을 수 있으며 이 포맷을 그대로 가져와 NeRO에서는 color를 2가지 형태로 예측하며 각각이 diffuse와 specular color를 의미한다고 말해준다. m, a, D, F, G와 같은 상수들이 등장하는데 코어 파라미터는 m, rho, a이고 이를 조합해서 나머지를 만들 수 있다고 해서 네트워크 출력으로 m, rho, a를 예측한다. |
  |
 첫 스테이지에서는 NeuS 뒤에 color network를 따로 달아서 diffuse와 specular를 예측하게 한다. 근데 앞서 BRDF 수식 (2)은 효과적으로 연산량을 줄이면서 성능 저하를 막을 수 있는 approximation 방법이 이미 밝혀져있다고 한다. 그 이름이 split-sum approximation인데 말그대로 integral 하나를 분리해서 intergral 두 개로 나뉘어진 형태로 만드는 것이다. 수식(7)과 같다. specular term이 간소화되는 것이고 diffuse term은 그대로다. |
 |
수식 간소화까지 했으니 그 안에 들어가는 variable을 살펴볼 차례다. 그 안에 들어갈 L()이 문젠데 이 것은 light로 direct/indirect light로 나뉜다. 각각 직접 light source에서 오는 빛, 어딘가에 부딪혀서 반사로 나오는 빛을 의미한다. 둘 다 네트워크가 맞추는 값으로 설정되어 있고 네트워크는 view direction을 spherical harmonic으로 encoding한 값과 position 정보를 받게 설계되어 있다.  정확히는 direct light는 지금 bounding sphere 외부에 빛이 있다고 볼 수 있으니 어느 point든 view direction만 맞으면 모두 같은 빛을 받을 수 있으므로, direct light MLP에는 point 정보는 안들어간다. |
 |
approximation이 split-sum 에 이어 한 번 더 들어간다. 바로 반사광의 반사 각도를 고정하는 것이다. 무슨 말이냐면, 위 그림처럼 반사광을 표면 재질에 따라 다양한 각도로 튕겨져 나간다. 그래서 이 모든 것은 반영하기 위해 intergral with omega가 수식에 껴있는 것이다. 하지만 계산 시에 mirror 처럼 t 하나 방향으로 모두 튕겨져 나간다고 간소화 한다. 추측컨대, occlusion probability, s()도 MLP인데 이게 integral 안에 있으면 모든 view direction 마다 MLP가 돌아야하니까 메모리를 너무 먹으니 integral 밖으로 꺼내기 위해 어쩔 수 없이 approximation한 것 같다. 이 approximation 여파로 성능이 떨어졌고 이를 보강하기 위해서 스테이지2가 추가된 것 같다. integral + omega를 t에 대한 1회 연산으로 간소화함으로써 수식을 간소화했다. diffuse term 역시 omega 대신 t를 씀으로써 일부 간소화할 수 있는 부분이 생긴다. |
  |
loss는 크게 2개다. occlusion loss 그리고 NeuS에서 사용하는 loss. occlusion loss는 그냥 냅다 학습을 해보니 아래 그림처럼 학습이 잘 안되고 occlusion probability가 제맘대로 나오는 현상을 보고 추가한 것이다. 핵심은 지금 어떤 한 지점 p을 지나가는 direct light든 튕겨온 indirect light든 rendering에 사용되는지 안되는지 분간해내는 것이다. 사용 안될 빛이라면 p에서도 occlusion probability 가 높고, p에서 튕겨져서 어딘가에 부딪힐텐데 그 부딪힌 위치에서도 occlusion probability가 높아야한다. 결국 안 보일 빛은 어느 지점에서 보아도 안보여야한다는 것이다. 이를 달성하기 위해 p마다 ray marching을 적용해서 튕겨져나간 빛이 어디에 부딪히는지 찾고 p와 부딪힌 위치 p'에서 occlusion probability가 갖도록 loss를 걸었다. 연산량 따윈 신경쓰지 않는 면모를 보인다. |
 |
또 하나 이슈가 있는데, 촬영 시 반사체를 찍는 것이기 때문에 표면에 촬영자가 보인다는 것이다... 촬영자가 이동하기 때문에 multiview contraint가 통하지 않는 요소다. 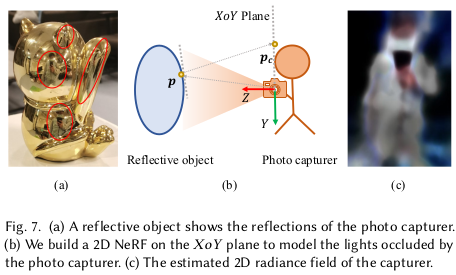 어떻게 해결했는가! 2D NeRF를 갖다붙였다... 촬영자가 카메라를 거의 고정적으로 들고 심혈을 기울여서 반사체 주변을 돌며 촬영했다는 가정 하에 카메라 plane을 연장한 평면에 반사된 사람만을 그려주는 2D NeRF를 학습했다. 연산량 따윈 역시 신경쓰지 않는 모습 |
 |
stage 1에서 BRDF 반사 ray의 다양한 각도 omega들을 단 하나의 t 각도로 approximation한 것을 stage 2에서 푼다. 이미 학습이 웬만치 되어있기 때문에 SDF 네트워크를 고정하고 BRDF에만 집중해서 finetune하는 컨셉이다. 앞서 추측한대로 연산량이 엄청날 것 같은데, finetune이니 약간의 시간만 투자하는 식으로 그냥 하는 것 같다. diffuse, specular를 나눠서 각각 특정 개수의 반사 각도를 평균내서 color를 만들고 color supervision을 주는 식으로 했다. 사실상 stage 1에서 approximation 전 형태의 discrete 버전이다. |
 |
stage 2에서 새로 등장하는 loss term은, BRDF를 건드는만큼 material에 집중되어있다. m, rho, a를 추측하는 네트워크에 걸어주는 regularization이다. 특정 위치는 그 주변부와 물성치가 비슷해야한다거나 diffuse 빛은 너무 화려하지 않고 gray 계열에 가까워야한다는 점을 이용한다. |
 |
 |
반응형
