[Linear algebra] 24-24b. Markov matrices; fourier series

*24b강은 퀴즈 해설 강의로 제외함

Lecture

https://ocw.mit.edu/courses/18-06-linear-algebra-spring-2010/resources/lecture-24-markov-matrices-fourier-series/

Lecture 24: Markov matrices; fourier series | Linear Algebra | Mathematics | MIT OpenCourseWare

 

Note

• eigenvalue/eigenvector의 활용에 관한 1개의 예시, markov matrix와 다소 동떨어져 보이지만 fourier series를 소개한다.

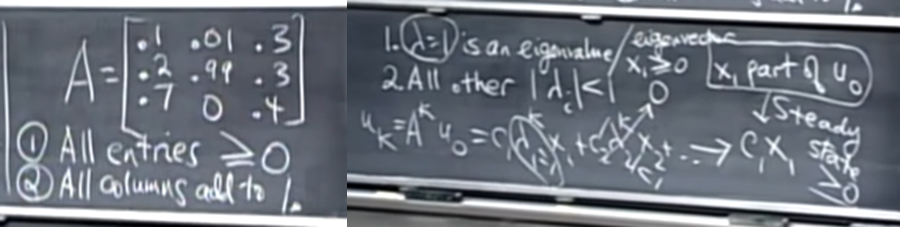
• Markov matrix는 위 사진의 A와 같이 column의 합이 1이 되며 모든 element가 양수인 행렬이다. 
• 이 행렬은 eigenvalue 중 하나가 반드시 1이 존재하며 그 나머지는 크기가 1보다 작은 특징을 갖는데 필연적으로 steady state로 향하는 행렬이다. 
• 이 때 eigenvalue 1에 대응되는 eigenvector는 양수이거나 0인 조건을 만족한다. 
  
  

• 위 조건들을 조금 더 관찰해보면 실제로 A-1I (eigenvalue가 1일 때)는 column 별 합이 0이 된다. 그 말은 row vector의 linear combination (1, 1, 1) 으로 0을 만들 수 있으니 row vector가 dependent하다는 말이고 이 말은 즉 A-I가 singular matrix라는 것을 알 수 있다. det(A-I)=0 이라는 말이 되기도 한다.
• (칠판 판서가 잘못된 것 같은데 N(A.T) 가 아니라 N( (A-I).T) 인 것 같고, N(A) 역시 N(A-I)일 것 같다.) 
• eigenvector x1은 (0.6, 33, 0.7)로 모두 양수이거나 0이라는 조건도 만족한다. (이건 증명을 안하고 넘어감)
  
  

• Markov matrix는 그래서 어디에 쓰이냐? 통계에서 자주 등장한다. 위 예시는 캘리포니아와 메사추세츠 두 도시 간의 인구 이동을 행렬화 한 것인데 인구의 총합은 항상 1이라고 보면 markov matrix 조건을 만족한다.
  
  

• 이 행렬을 갖고 u_k+1 = A_k u_k 를 풀게 되면 k년 후 인구 분포에 대한 예측이 가능해진다. (eigenvalue가 1이니 steady state에 도달한다는 것을 알고 있으니 말이다.) 1000/3 [2, 1] 에 수렴한다.
  
  

• 또 다른 주제는 fourier series인데 소개하기 전에 orthonormal basis로 이루어진 공간에 대해서 recap하는 시간을 갖는다. 
• 위와 같이 orthonormal basis q1~q_n 을 갖고 있을 때, n차원 공간 내 vector v는 (x1, x2, x3, ...)의 linear combination으로 표현할 수 있고 이 때 x1, x2, ... 각각을 얻고 싶으면 대응되는 basis를 dot product해주면 된다. 
  
  

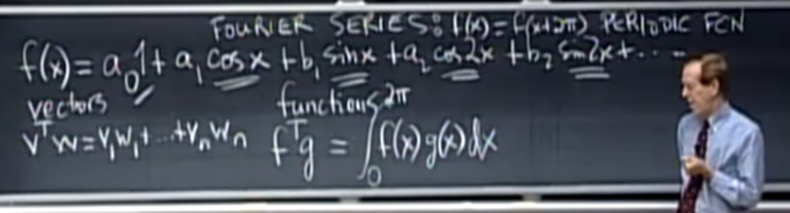
• fourier series 식은 위와 같은데 정확히 같은 꼴을 갖고 있음을 알 수 있다. 
• q1 ~ q_n 이 마치 (1, cos(x), sin(x), cos(2x), sin(2x), ...)와 같은 orthonormal matrix로 표현할 수 있다. 
• 다만 q_n이 vector가 아닌 function이라는 차이가 있을 뿐이다. 
• 공간에서 continual한 function은 dot product 개념을 정의하길, 연속 공간에서 모든 위치에서 곱을 더한 것이므로 위 사진에서처럼 intergral을 포함한 형태로 적힌다.
• 따라서 fourier series도 결국 행렬 연산으로 풀 수 있는 문제임을 알려준다.