반응형
Lecture
Lecture 26: Complex matrices; fast fourier transform | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note
- complex number라는 키워드가 eigenvalue/eigenvector를 공부하는 중간에 등장한 김에 강의 1개를 complex domain의 행렬은 어떤 특징이 있는지, 대표적 예시가 무엇이 있는지 설명하고자 하는 것 같다.
- complex number로 이루어진 matrix를 다루는 것은 실생활에서 흔하지 않을 것 같지만 real matrix를 다룰 때에도 eigenvalue/eigenvector는 complex number가 될 수 있으므로 이해하고 있어야 한다.
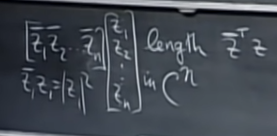
- 가장 간단하게, complex number가 포함된 벡터는 그 크기를 구할 때 일반 실수 벡터처럼 transpose와 dot product하는 것으로 구할 수 없다. conjugate+transpose와 dot product해야 얻을 수 있다.
- conjugate+transpose 조합은 자주 쓰여서 따로 hermitian 정의하고 H로 표기한다.

- complex domain에서는 symmetry와 perpendicular의 개념도 바뀐다. symmetry는 hermitian(conjugate+transpose)를이 원본과 같아야 한다. perpendicular 역시 Q.T Q= I 가 아니라 Q.H Q = I 를 만족해야 한다. (그리고 perpendicular가 아니라 unitary라고 부른다.)

- FT(Fourier transform)은 n차원 벡터에 Fn, fourier transform matrix를 곱하는 것으로 쉽게 할 수 있다. (fourier series랑 헷갈리지 말자.)
- Fn은 위와 같이 생겼는데 Fn의 i th row, j th column 값 (Fn)ij 는 w^(ij) 이며 그 w는 칠판에 적혀있는 것처럼 exp(i2pi/n)이다.
- 이를 복소평면에 그리면 w는 복소평면 상 단일 원 위의 한 점이고 w의 제곱들은 그 단일 원 위를 뱅글뱅글 도는 또 다른 점들이다. (칠판에 있는 그림은 n=6일 때다.)
- complex matrix의 대표적 예시가 FT matrix다.

- n이 4일 때 주목할만 하다. F4를 써보면 우측 사진과 같이 1과 i로만 이루어진 깔끔한 matrix임을 알 수 있는데 이 F4는 모든 column이 orthogonal(크기를 맞추면 orthonormal) 하다.
- 직접 계산해보면 모든 column의 dot product가 0이 되기 때문이다. (i가 껴있으면 conjugate를 잊지 말자.)
- 그래서 F4는 F4.H = F4.inv를 만족하는 아주 깔끔한 형태다.
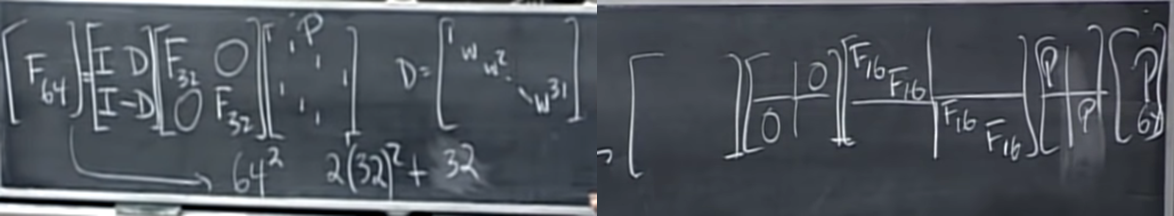
- FFT(Fast fourier transform)을 더 많이 들어봤을 법한데 그 이유는 F n은 F n/2의 조합으로 표현할 수 있기 때문이다.
- 위에서 FT matrix 내부의 w는 복소평면에서 단일 원 위에서 그릴 수 있다고 했다.
- 그 그림을 상상하면서 생각해보면 w32 (n=32) 는 w64의 제곱과 같은 위치라는 것을 알 수 있다. 수식에 대입해도 값이 같다는 것을 단번에 알 수 있을 것이다.
- 그 말인 즉슨 w64가 내부에 가득찬 F64는 w32가 가득찬 F32의 조합으로 표현이 가능하다는 말이다. 물론 아주 단순하게는 아니다.
- 좌측사진을 보면 그 구체적인 형태가 나와있는데 F64는 [F32가 대각성분, 나머지는 0] 인 64x64 행렬을 중앙으로 두고 앞에는 [Identity, Diagonal]행렬 뒤에는 [홀수만 뽑는 permutation, 짝수만 뽑는 permutatino] 행렬이 붙은 형태로 표현이 가능하다.
- [Diagonal]은 좌측 사진처럼 대각 성분에 w가 점점 차수가 높아지면서 적혀있는 모양이다.
- Fast라는 이름이 붙은 이유는 이렇게 decomposition할 경우, 연산의 횟수가 어마어마하게 줄기 때문이다.
- 만약 F64를 그대로 64차원 벡터에 곱한다고 하면 컴퓨터는 64^2의 곱셈을 해야하지만, 이렇게 쪼갤 경우 2(32^2)+32 의 곱셈만 하면 된다.
- F64를 F32의 조합으로 쪼개는 것에서 멈추지 않고 끊임없이 쪼개어 F1에 도달한다고 하면 연산 횟수는 드라마틱하게 더 줄어든다.
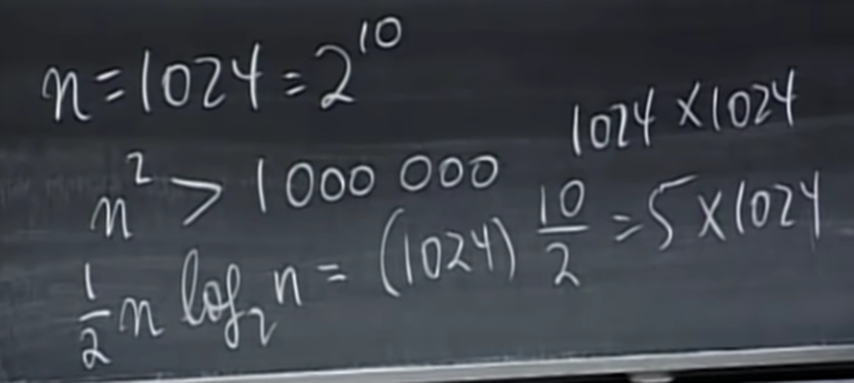
- 계산해보면 대충 Fn은 줄이고 줄여서 n^2가 아닌 1/2 n log2 (n) 까지 줄일 수 있다.
- n=10일 때를 계산해보면 1024*1024 회에서 5*1024로 줄이는 엄청난 연산량 감소다.
- 이러한 특징 때문에 FFT가 더 유명한 것이다.
- 이번 강의는 중간에 뜬금없이 등장했지만 약간 complex matrix도 재밌고 의미가 있다는 메시지를 던지려고 한 교양 강의 같다. 그냥 그렇구나 받아들이고 넘어가면 될 듯 하다.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 28. Similar matrices and Jordan form (0) | 2023.02.04 |
|---|---|
| [Linear algebra] 27. Positive definite matrices and minima (0) | 2023.02.04 |
| [Linear algebra] 25. Symmetric matrices and positive definiteness (0) | 2023.02.02 |
| [Linear algebra] 24-24b. Markov matrices; fourier series (0) | 2023.01.30 |
| [Linear algebra] 23. Differential equations exp(At) (0) | 2023.01.29 |