카메라 자세를 초기화할 때 가장 많이 쓰이는 방법이 PnP를 사용하는 것이다. 이미 알고 있는 3D point set과 이미지에서 검출한 2D point set이 있을 경우, 수학적으로 자세를 아주 간단하게 구할 수 있고 심지어 opencv 함수로 구현되어 있기 때문에 단 한 줄이면 카메라 자세 값을 계산할 수 있다.
하지만 카메라가 광각 카메라여서 pinhole model로 표현이 안될 경우에는 이러한 접근이 어렵다.
PnP 알고리즘은 3D point와 2D point 간의 관계가 서로 linear projection일 경우를 가정하기 때문이다. 다른 말로 표현하면 빛이 직진해서 바로 이미지로 맺혔을 경우에만 적용이 가능하다.
반면 광각 카메라 (특히 180도가 넘어가는) 의 경우, 2D point와 3D point 간의 관계가 linear하지 않다. 빛이 굴절의 굴절을 거듭하여 맺힌 non-linear projection 관계이기 때문에 PnP를 풀 수 없다.
그럼 광각 카메라는 자세 초기화를 간단히 PnP 알고리즘을 할 수 없나? 아니다.
약간의 2D point 전처리를 해준다면 그대로 적용할 수 있다.
이 글에서는 광각 카메라로 촬영한 이미지를 갖고 PnP를 풀 수 있는 트릭을 소개하고자 한다.
광각 카메라의 픽셀 바라보기
먼저 앞서 말한 듯 광각 이미지 픽셀이 담고 있는 빛은 굴절된 빛이다. 이 예시에서는 double sphere model을 가정할 것인데 다음 그림을 보면 무슨 말인지 쉽게 이해할 수 있을 것 같다

따라서 2D point를 그대로 back projection하면 3D point에 맺히지 않는다. 굴절 관계를 반영해서 back projection 해야만 3D point에 닿을 수 있다.

위 그림과 같이 실제 공간에 녹색 3D point들이 있다고 생각해보자. 이 녹색점들이 카메라 중심을 향해 linear projection 됐다면 파란점과 같이 구 형태로 맺혔어야 한다.
하지만 광각 카메라든 일반 카메라든 결국 평면으로 제작된 이미지 센서에 빛을 모아서 이미지 형태로 표현을 해야만 하므로 최종적으로 카메라 projection 모델에 따라 빨간 2D point로 저장된다.
우리가 보는 이미지 상 2D point들은 위 그림에서 빨간색 점들에 해당하는 것으로 빨간색 점과 녹색 점 간의 관계가 linear하지 않다는 것은 단번에 시각적으로 알 수 있을 것이다.
따라서 빨간 2D point 와 녹색 3D point 간의 PnP 알고리즘은 성립할 수가 없다.
픽셀에서 Ray로, Ray에서 normalized image plane으로

그렇다면 우리가 관찰하고 있는 2D point를 일단 3D point와 linear projection 관계인 파란색 point로 옮겨주는 작업이 선행되어야 한다.
다행히 빨강 to 파랑은 각 광각 카메라 모델 (UCM, EUCM, DS etc) 각각 다 정의되어 있으므로 쉽게 구할 수 있다. 다시 말해 unproject하면 된다.
그 다음은 파랑 point (이하 ray)를 연장해서 z값이 1이 되도록 연장한다!
[rx, ry, 1]과 같이 표현된 ray를 다른 시선에서 보면 focal length가 1인 image plane에 맺힌 2D point들이 된다.
즉, 우리가 PnP 알고리즘 적용하던 pinhole camera일 때와 같은 상황이 된 것이다.
다만 차이점은 normalized image plane에 바로 맺힌 2D point이기 때문에 intrinsic parameter가 필요없다.
다시 말해, focal length 1, principal point (0,0), zero distortion인 pinhole 카메라와 같은 상황이다.
ret, rvec, tvec = cv2.solvePnP(pt3ds, normalized_ray[:, :2], np.eye(3), np.zeros([5]))
따라서 solvePnP 함수 내에 mtx, distortion coefficient를 위와 같이 변경해주고, 2d point 위치에 z 값이 1로 normalize된 ray의 x, y 값을 사용하면 된다.
말로만 하면 이게 무슨 소린지 이해가 잘 안 갈테니 아래와 같이 그림을 그려봤다.
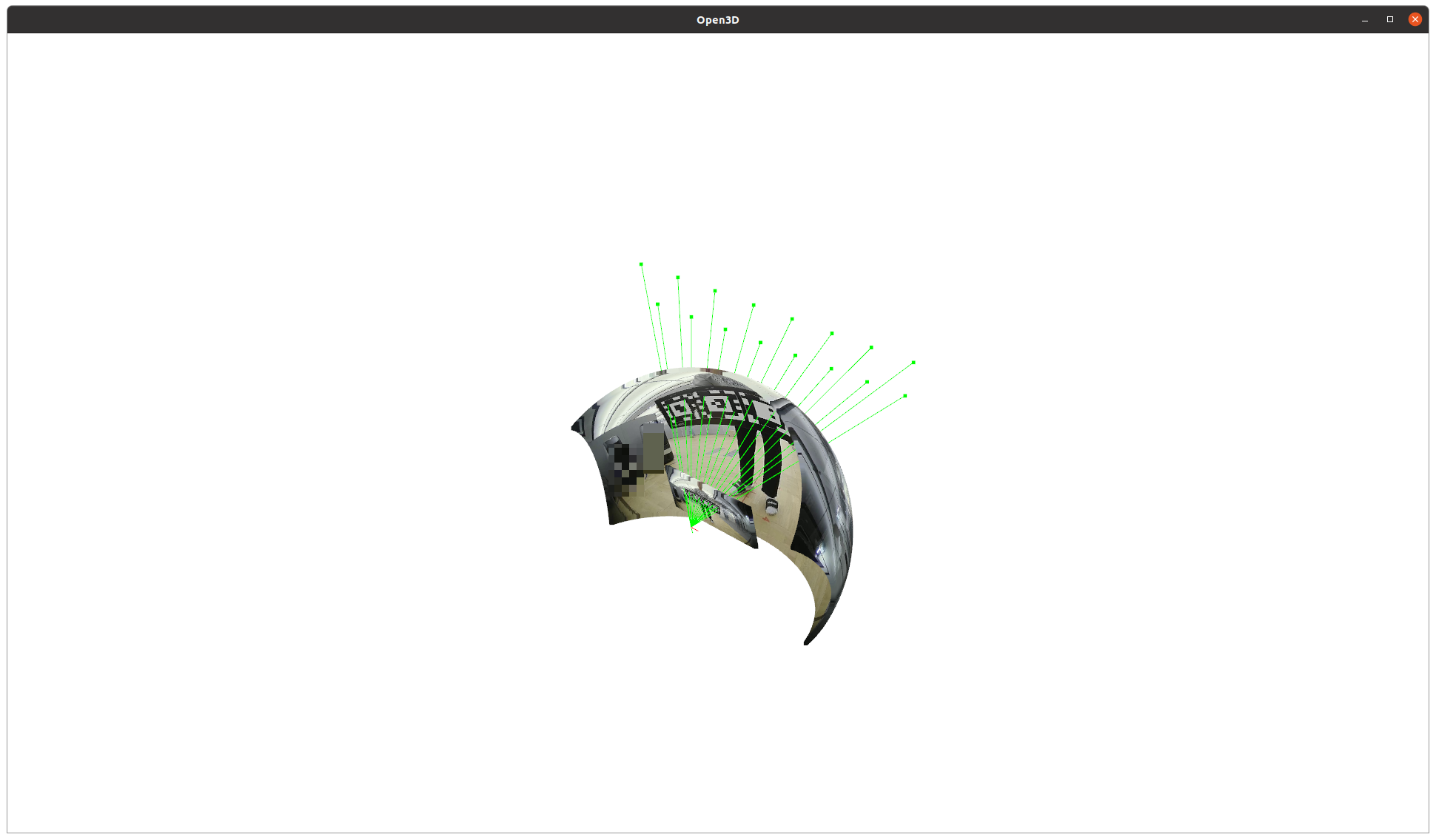
광각 이미지를 unproject해서 3d point와 linear projection 관계를 갖는 sphere image로 만든다. 그리고 2D point(ray)를 z값 1이 되도록 normalize하면 focal length 1인 이미지 평면에 맺힌 것과 동일해진다.
이 상태에서 저 녹색점(x,y 값만)들과 알고 있는 3D point 간의 PnP를 푸는 것이다. 이러면 PnP 알고리즘이 동작 안할 이유가 없다!
코드 예시는 다음과 같다. (double sphere model unprojection 함수를 사용했다.)
import os
import json
import cv2
import numpy as np
def solve(cam_params, pt2ds, pt3ds):
fx = cam_params["fx"]
fy = cam_params["fy"]
cx = cam_params["cx"]
cy = cam_params["cy"]
xi = cam_params["xi"]
alpha = cam_params["alpha"]
mtx = np.eye(3, dtype=np.float64)
dist = np.zeros([5], dtype=np.float64)
x = (pt2ds[:, 0] - cx) / fx
y = (pt2ds[:, 1] - cy) / fy
r = np.sqrt(x ** 2 + y ** 2)
z = ((1 - alpha ** 2 * r ** 2) / (
alpha * np.sqrt(np.clip(1 - (2 * alpha - 1) * r ** 2, a_min=0, a_max=None)) + 1 - alpha))
xyz = np.concatenate([x[:, None], y[:, None], z[:, None]], axis=1) # check the norm
xyz = ((z * xi + np.sqrt(z ** 2 + (1 - xi ** 2) * r ** 2)) / (z ** 2 + r ** 2))[:, None] * xyz
xyz[:, 2] -= xi
rays = xyz / np.linalg.norm(xyz, axis=1)[:, None]
rays = rays / rays[:, 2:3]
pt2ds_ud = rays[:, :2]
ret, rvec, tvec = cv2.solvePnP(pt3ds.astype(np.float64), pt2ds_ud.astype(np.float64), mtx.astype(np.float64), dist.astype(np.float64))
rvec = rvec.squeeze()
tvec = tvec.reshape(-1)
return rvec, tvec
if __name__ == '__main__':
img = cv2.imread(os.path.join(img_dir, img_name))
img_gray = cv2.cvtColor(img0, cv2.COLOR_BGR2GRAY)
pt2ds = DETECTED_TAG2D_POINTS
pt3ds = KNOWN_TAG3D_POINTS
cam_params = {
"xi": 1.5204921523974696e-8,
"alpha": 0.5371038903675522,
"fx": 374.86238538857256,
"fy": 376.23547645085457,
"cx": 631.3346876250283,
"cy": 364.153174184717
}
rvec, tvec = solve(cam_params, pt2ds0, pt3ds0)
간단한 트릭만으로 광각 카메라 자세 추정을 처음부터 구현할 것 없이 기존 PnP 알고리즘을 활용해서 해결할 수 있다!
주의사항
하나 주의사항이 있다. 위에 설명한 내용/트릭은 이론 상 오류가 없기 때문에 수학적으로는 광각 카메라 자세도 일반 카메라 자세만큼이나 정확히 PnP로 풀려야 한다.
하지만 실상은 그렇지 않다. 왜 그러냐고 하면, 한 픽셀이 표현할 수 있는 정확도 측면에서 광각 카메라가 압도적으로 불리하기 때문이다.
직관적으로만 보아도, 같은 이미지 센서에 180도 화각이 넘는 빛을 모을 때와 100도 화각의 빛을 모을 때 후자가 더 표현 능력이 널널할 것이다. 한 픽셀이 표현해야 할 빛이 적다는 소리다.
특히 볼록한 이미지로 저장되는 광각 이미지 특성 상 이미지 외곽 (150도 이상~)은 한 픽셀이 표현해야 하는 빛이 너무 많다. 다른 말로 분해능이 부족하다.
따라서 아래 두 경우에 광각 PnP의 성능은 다르다.
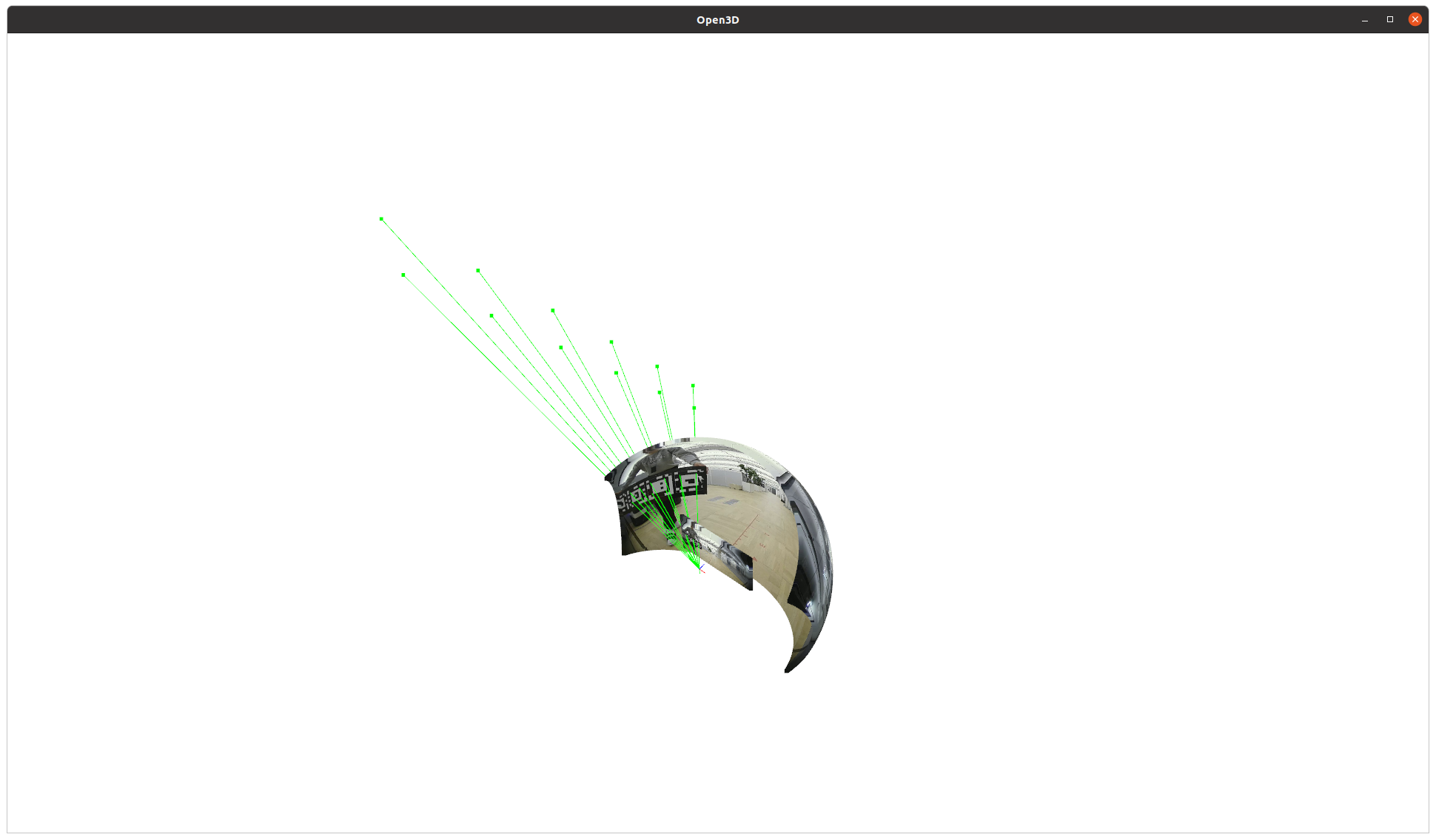

픽셀 분해능이 조금 이라도 뛰어난 후자가 더 정확한 자세 추정 결과를 갖는다.
예시
두 카메라 간의 extrinsic을 계산하기 위해 광각 PnP를 활용한 예시다.
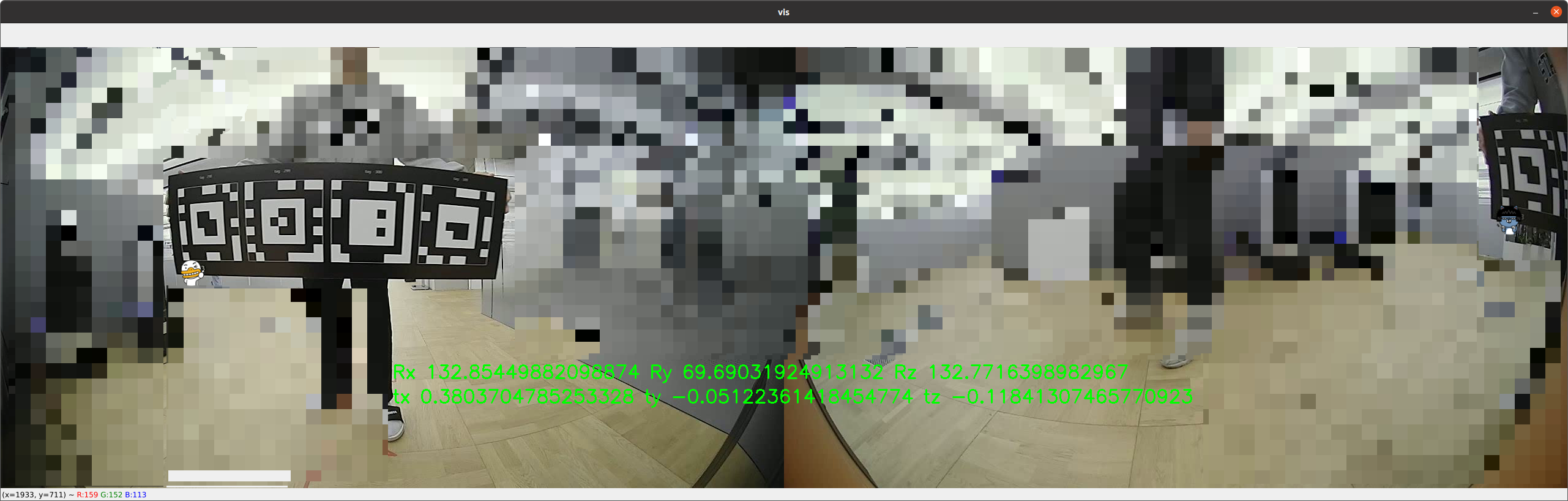
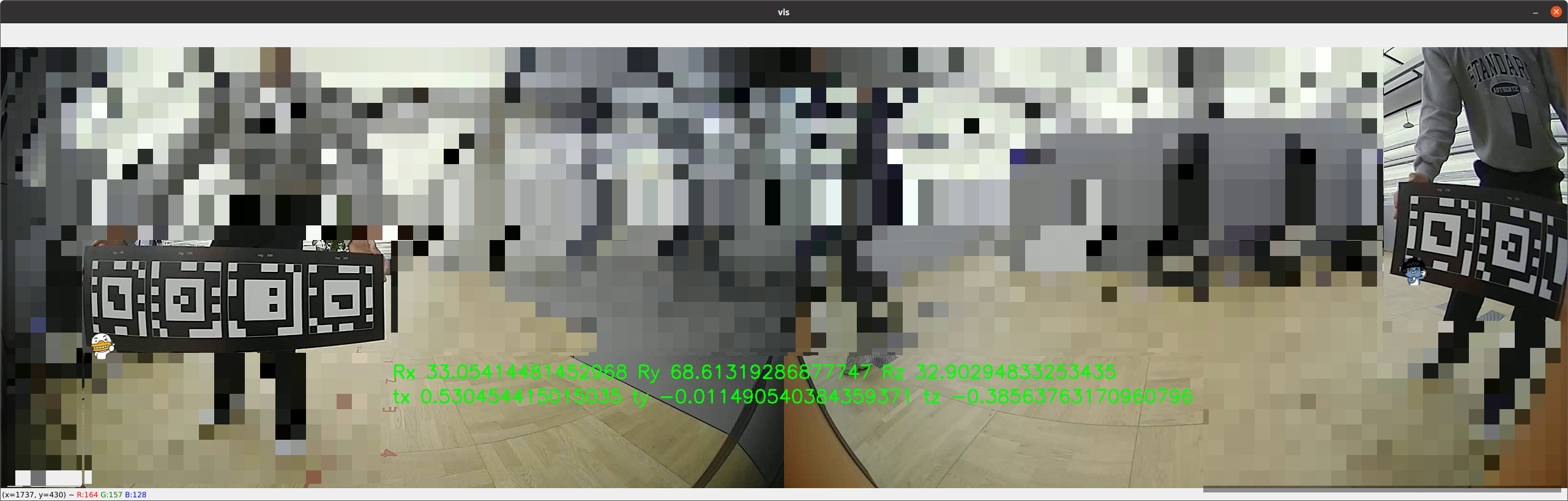
위 사진과 같이 별로 크게 움직이지도 않았는데 이미지 외곽으로 2D point가 이동했다는 이유만으로 결과가 달라진다.

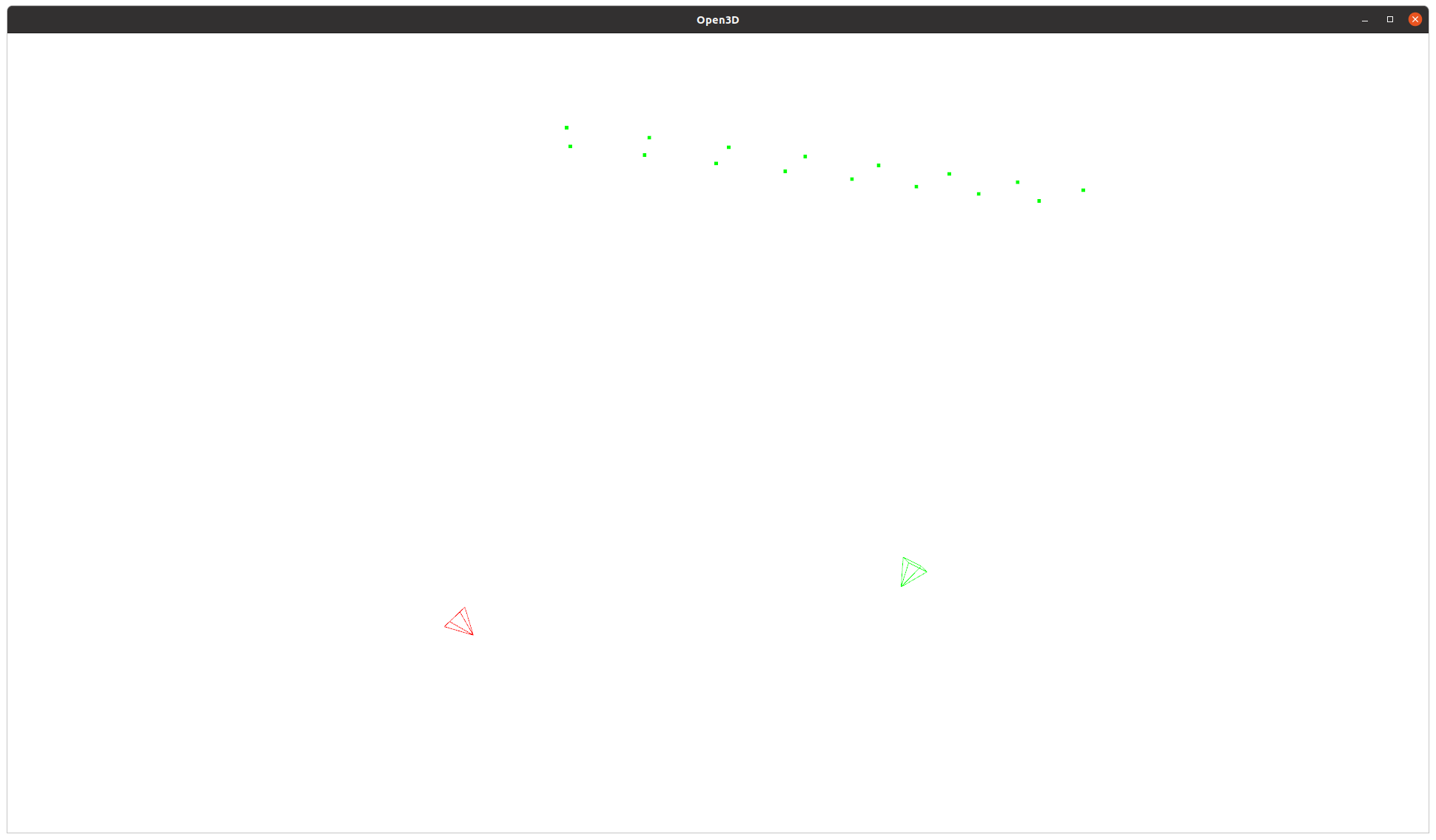
이 정도면 믿고 쓰지 못할 정도로 흔들린다고 봐도 무방하다. 웬만하면 이미지 외곽에서 포인트를 잡으면 안된다.
파훼법은 없나? 없다. 이건 픽셀 분해능 문제이므로 물리적으로 발생하는 현상이라 이를 반영한 최적화 코드를 따로 구현하지 않는 이상 극복할 수 없다.
완화법은 그나마 point를 많고 넓게 쓰는 것이다.
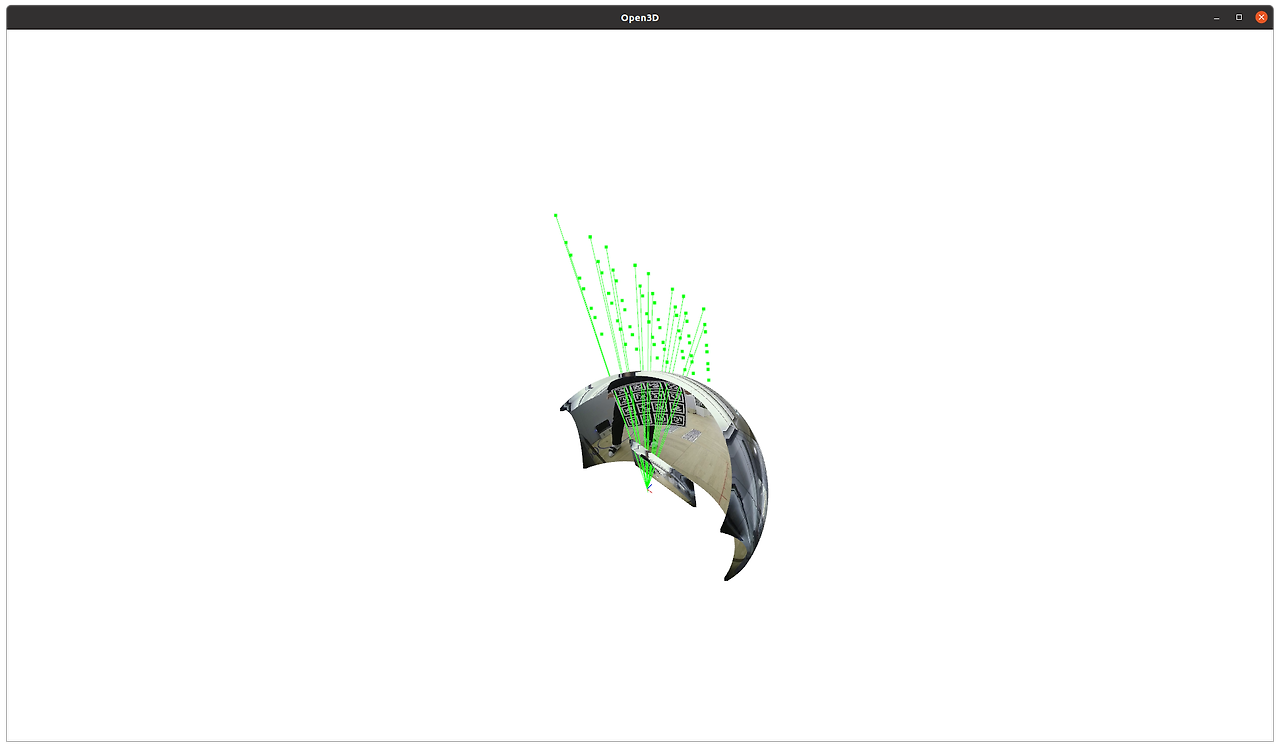
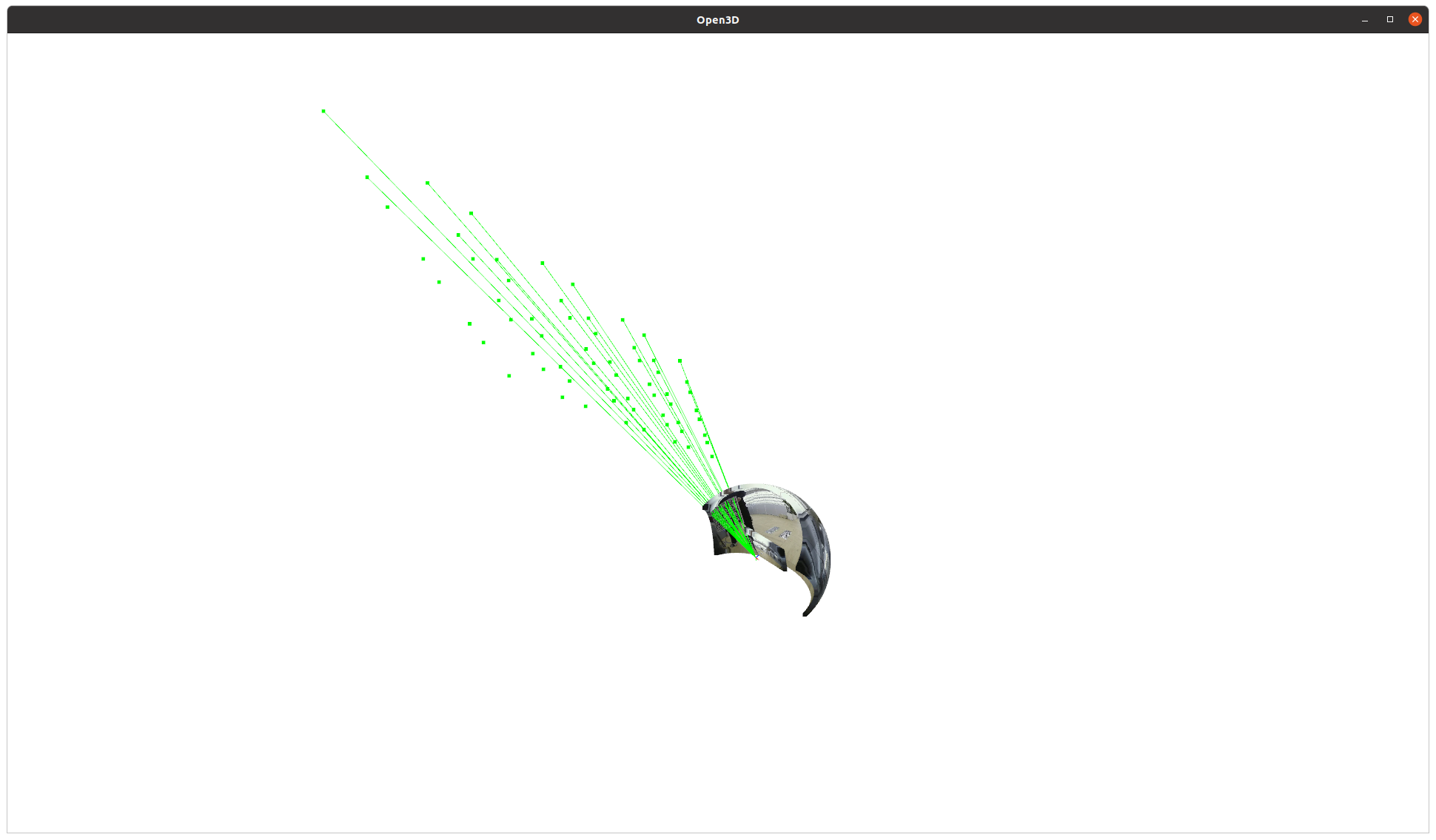
만약 point를 더 확보할 수 있으면 위 그림만 봐도 직관적으로 알 수 있듯이 분해능 부족을 candidate 추가로 완화할 수 있다.
'Knowhow > Vision' 카테고리의 다른 글
| COCO bounding box format, scale factor (0) | 2024.04.25 |
|---|---|
| Double sphere 모델 projection-failed region (0) | 2024.02.28 |
| COLMAP[python] pycolmap 보다 편하게 colmap 사용하기 (0) | 2023.12.07 |
| RealityCapture camera coordinate to opencv(vision) camera coordinate (0) | 2023.12.06 |
| Open3d를 이용한 디버깅용 camera, bbox, origin visualization (0) | 2023.12.06 |