이전 글 3D transformation(R, t) matrix notation 에서 SE3 4x4 matrix가 주어졌을 때 notation을 어떻게 표기하고, 그 notation을 해석하는 방법을 적은 바 있다.
해당하는 부분만 발췌해보면 다음과 같이 표기했을 때,
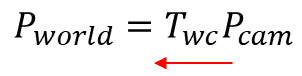
1) 우측 좌표계에서 좌측 좌표계로 변환하는 transformation matrix라고 해석한다.
- 예) 3D point들을 camera 좌표계(c)에서 world 좌표계(w)로 변환한다. 결과적으로 world coord. 3D point가 나옴.
2) 왼쪽 좌표계에서 바라본, 우측 좌표계의 축, 원점 이라고 해석한다.
- 예) world 좌표계(w)에서 바라본 camera 좌표계의 원점, 축들의 rotation, translation이다.
- 즉, world 좌표계(w)에서 바라본 camera(c)의 자세라고 해석할 수 있다.
총 2가지 해석이 가능하다고 했었다. 다시 말해 어디서 어디로 좌표계가 변하는지, 어디서 어떤 카메라를 바라보는지로 해석할 수 있다고 했다.
하지만 실제로 SE3 matrix를 다루다 보니 추가적으로 알고 있으면 좋을 해석이 있어서 정리하고자 한다.
사실 SE3 4x4 matrix는 transformation matrix 자체일 뿐이기 때문에 여러가지 해석을 붙이는 것이 의미가 없을 수도 있는데 개발하는 입장에서는 외워두면 좋을 "생각의 흐름" 정도로 여기면 될 것 같다.
3) notation이 없을 경우, 좌표계 변경 없이 회전, 이동하는 transformation matrix라고 해석한다.
예를 들면, 그냥 지금 갖고 있는 카메라를 90도 돌리고 싶을 때다. 이 경우 좌표계가 바뀌는 것도, 바라보는 카메라가 바뀌는 것도 아니다. (물론 그렇게 해석할 수도 있다.)
오히려 notation으로 표기하면 어떻게 적을 수 있을지 신경쓰면서 생각하면 더 헷갈린다. 그냥 새롭게 외워버리는게 빠르다.
구체적으로 더 설명해보면, 아래 camera pose, T_wc 가 주어졌다. 2)에 의해 world coord.에서 바라본 camera pose, c가 된다.
이 때 world coord. 기준으로 z축으로 카메라를 +90도 회전시키고자 T matrix (yaw 90도 회전) 을 곱해준다고 하자.
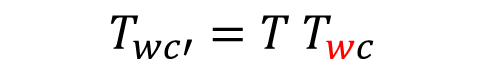
그럼 위와 같이 적을 수 있을 것이다. 기존 camera pose, c에서 90도 회전된 뒤의 camera pose, c'가 되는 모양이다.
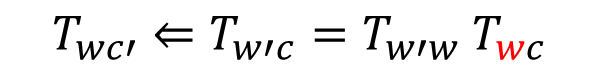
이걸 굳이 notation을 적어가면서 표현을 하고자 하면 상당히 난해해진다. 역으로 90도 회전된 새로운 world coord. w'로 camera를 옮긴 뒤, w'를 기존 w와 동일하게 사용하는 식으로 생각해야 한다. (적는 것도 난해하다.)
따라서 이렇게 그냥 순수하게 회전과 이동을 가하고 싶어서 transformation matrix를 다룰 때는 notation을 신경쓰지 않고 별도의 연산처럼 생각하는 것이 좋다.
3)의 경우, notation 대신 신경써야 할 것이 오히려 있는데 바로 앞에 곱하냐 뒤에 곱하냐의 차이다.
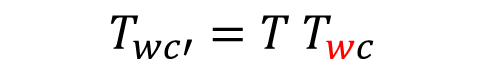
- 앞에 곱할 경우, 뒤에 따라붙은 transformation matrix의 앞 notation 좌표계에서 회전, 이동한다.
- 위와 같이 적혀있으면, world 좌표계 기준으로 90도 회전시키고자 하는 것이다.

- world coord.(x, y, z축이 각각 R, G, B 축으로 표시)를 기준으로 기존 카메라 (빨간색)을 90도 회전시키는 모양(파란색)이 된다.
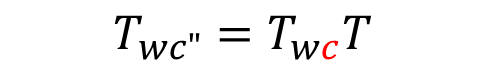
- 뒤에 곱할 경우, 뒤에 따라붙은 transformation matrix의 뒤 notation 좌표계에서 회전, 이동한다.
- 위와 같이 적혀있으면, camera 좌표계 기준으로 90도 회전시키고자 하는 것이다.

- camera coord. 를 기준으로 기존 카메라 (빨간색)을 90도 회전시키는 모양(초록색)이 된다.
정리해보면, camera-global, camera-camera 간의 좌표계 변환 관계가 연관되어 있어 notation 표기가 되어 있는 경우에는 1) 2)와 같이 2가지 의미로 해석하면 되고 좌표계 변환과 연관없이 순수하게 회전,이동에만 관여하는 경우에는 3)과 같이 곱하는 위치에 따라 기준 좌표계가 달라지는 것으로 해석하면 되겠다.
'Knowledge > Vision' 카테고리의 다른 글
| Spherical gaussian 직관적으로 이해하기 (0) | 2023.12.21 |
|---|---|
| Spherical harmonic 직관적으로 이해하기 (0) | 2023.11.23 |
| Static library와 dynamic library 차이 (0) | 2023.09.14 |
| Positional embedding (직관적 이해) (0) | 2023.09.13 |
| Image flickering (0) | 2023.08.17 |