Spherical harmonic이라는 용어가 NeRF를 비롯한 논문들에 자주 등장하는데 정작 의미는 몰라 조금 정리를 해보고자 한다.
개념 자체의 출처가 수학과 물리학이다보니 모든 내용을 파고 들어 이해하는 것은 과한 것 같아, computer graphics에서 활용하는 이유를 받아들일 수 있을 정도로만 얕은 이해를 해보기로 했다.
일단, Spherical hormonic (이하 SH)를 이해하기 위해서 필요한 최소한의 수학과 직관으로부터 시작해보자!
STEP 0 : 라플라스 방정식 개념
SH의 시작은 라플라스 방정식을 구면 좌표계에 적용해보는 것이다. 왜 굳이 구면 좌표계에 적용했냐? 라고 그 이유와 의미를 묻는다면...원래 수학이라는게 의미부여 이전에 개념을 정의하는 레벨이기 때문에 그냥 이렇게 해본 것에는 아무 이유도 의미도 없다. 수학에 의미를 부여하는 건 물리로 넘어와 실제 활용을 할 때니까 말이다.
아무튼 구면좌표계에 라플라스 방정식을 정의해본 것이 시작이다.
일단 라플라스 방정식이란 간단하다. 아래 수식과 같이 두 번 미분한 값이 0이 된다는 방정식이다.

여기서 f가 구면 좌표계에 정의된 위치다. 그냥 구 표면의 위치 하나하나라고 생각하면 되겠다. 구 표면의 위치 f는 한 번 미분하면 구면이므로 constant값이 나올 것이고 두 번 미분하면 당연히 0이 될 것이니 위 수식을 단번에 만족하는 대상이다.
(구면 좌표계에 라플라스 방정식을 적용했다는 것도 맞는 말이지만, 구면 좌표계가 애초에 라플라스 방정식을 만족하는 형태다.)
이것이 갖는 의미는 뭘까? 구면 좌표계를 정의하는 파라미터 (r,θ,ϕ)가 주어졌을 때 이것이 표현하는 위치 f가 있을 것인데 (r,θ,ϕ)과 f 간의 관계를 찾아낼 수 있는 방정식이 된다.
물론 (r,θ,ϕ)를 어떻게 지지고 볶아아 3차원 위치가 되는지 쉽게 알고 있다만 수학적으로 그렇다는 것이다.
STEP1 : 라플라스 방정식 전개
(자세한 내용은 링크에 자세히 나와있다. 여기선 필요한 부분만 기록했다.)
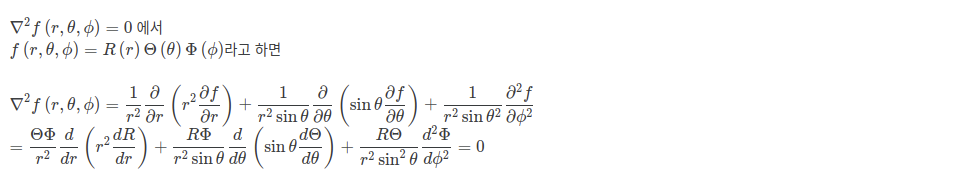
양변에 특정 값을 곱하고, 변수 분리를 취하는 과정을 거쳐 정리를 쭉 진행하면,

l 이라는 상수가 도입되는 형태를 거쳐

최종적으로 위와 같은 형태에 도달한다.
즉, 의미를 보면 r,θ,ϕ가 주어졌을 때 해당 위치 값 f(r,θ,ϕ)를 얻어내는 방법은 l, m으로 정의된 함수 P, Q에 (r,θ,ϕ)를 정해진 순서대로 곱해주면 얻을 수 있다. (+ 다 더하기)
STEP2 : 라플라스 방정식 결과 해석
수식 전개가 어려웠고 이해는 완벽히 안돼도 괜찮다.
여기서 주목할 점은 (r,θ,ϕ) -> f로 연결해주는 P와 Q가 전개 과정에서 등장한 상수 l, m에 의해서만 정의될 뿐, (r,θ,ϕ) 중 그 어느 하나와도 연관되어 있지 않다는 점이다. 그리고 l,m에 따라 만들어지는 각기 다른 P,Q는 서로 orthogonal하다는 특징이 있었다.
다시 말하면 P와 Q는 구면 좌표계를 표현하는 basis function과 같은 셈인 것이다.
cos, sin으로 표현되어 있어서 P, Q 두 개의 변수로 표현됐지만 e를 이용해 표현하면 다음과 같이 간소화하는 과정을 거치면,

Y라는 구면 좌표계 basis function을 얻어냈다고 해석할 수 있다.
단순히 구면 좌표계에 라플라스 방정식을 정의해본 것인데 여기서 수학적으로 의미있는 basis function를 결과적으로 얻어낼 수 있었다.
 |
|
 |
 |
위 그림이 basis function, Y를 l, m에 따라 시각화한 것인데 각자 독립적인 모양을 하고있다. 모양을 다르지만 360도 모든 각도를 표현하고 있다는 것을 알 수 있다.
STEP3 : Spherical harmonic의 등장
위에서 얻은 구면 좌표계의 basis function, Y를 활용해먹은 사례가 Spherical harmonic이다.
basis function을 알아냈으니, 그럼 구면 좌표계에 정의된 어떤 scalar field도 이 basis function을 이용하면 손쉽게 표현할 수 있겠네? 라고 생각해본 것이다.

scalar field(potential field)가 뭔지 이해하기가 어려울텐데 예시를 들어보면 상상하길, 뜨거운 쇠구슬 하나가 있고 쇠구슬의 위치마다 온도가 각각 다르지만 시간이 지나도 온도가 일정하다. 즉, 영원히 유지되는 뜨거운 구체가 하나 있다.
변하지 않는 위치위치마다 온도는 scalar다. 이 scalar(한 곳의 온도)가 구면 좌표계에 걸쳐 연속적으로 존재하니까 쇠구슬 전체의 온도는 scalar field라고 볼 수 있을 것이다.
이 때 (r,θ,ϕ) 가 주어지면 해당 위치의 온도를 알고 싶을 때, (r,θ,ϕ) -> temperature 간의 함수를 정의할 때 basis function을 활용할 수 있지 않을까? 라고 생각한 것이다.
결론부터 말하면 실제로 쉽다. basis function 마다 coefficient를 부여하기만 하면, 구면 위의 어떤 scalar 값도 표현할 수 있다.
다시 예시로 돌아가면, 각 basis function에 특정 coefficient를 잘 부여해두었다면, 구면 위의 온도를 계산하는 것은 아주 쉽다.
더 쉽게 말하면, 대충 첫번째 basis function은 4배, 두번째 basis function은 2.5배, 세번째 basis function에는 1.7배 ... 이렇게 조합하면 현재 쇠구슬 온도 분포를 모두 표현할 수 있다! 라고 할 수 있게 된다.
이러한 과정이 가능하다는 것을 개념화한 것이 Spherical harmonic이다. 한 마디로 정의하면 SH는 다음과 같이 말할 수 있다.
구면 좌표계에 라플라스 방정식을 적용해서 얻어낸 결과에서 basis function을 뽑아내고 이 basis function을 이용해 구면 상에 정의되는 scalar 값을 coefficient 만으로 표현할 수 있게 만드는 것!
그 의미는 다음과 같다.
1) 구면에 존재하는 무한개의 scalar, 즉 scalar field를 coefficient만으로 표현할 수 있다. (encoding 기능)
2) basis function 일부만 사용할 경우, 정보 손실은 있지만 여전히 표현할 수 있음 (compression 기능)
STEP 4 : Spherical harmonic의 활용
Spherical harmonic은 유명해진 계기가 컴퓨터 그래픽스에서 색상을 표현할 때 활용하면서 부터다.
색상은 분명하게 scalar value이고, 그래픽스에서는 빛 때문에 보는 방향에 따라 색상이 다를 수 있다는 점을 고려해야만 했고 (θ,ϕ)에 따라 변화하는 색상을 encoding할 수 있어야 했는데 SH가 딱이었다.
 |
 |
basis function이 위와 같이 독특한 모양을 갖고 있는데, 모양 별로 색상 팔레트를 부여하기만 하면 SH로 색상 표현이 가능했다.
왼쪽 그림처럼 SH basis function 모양이 각 방향으로 갖고 있는 크기, phase( 뭘말하는지 잘은 모르겠음) 등등을 RGB 색상에 대응시켜서 우측 그림처럼 color basis function으로 만드는 것이다.
이후에 똑같이 coefficient를 바꾸어 가면서 color basis function을 더해주면 구면 위의 모든 색상을 단 몇개의 coefficient만으로 표현이 가능하다.
STEP 5: 예시
SH를 색상 표현에 직접 활용한 예시는 Plenoxel이 대표적이다.

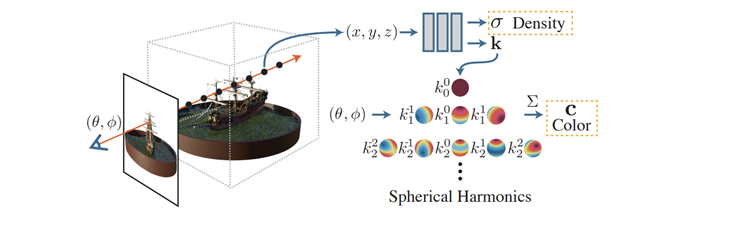
공간에 색상을 부여해야 하는데 view depedent color를 부여해야 하는 상황이었다. 이때 단순히 공간에 R,G,B 값만을 채운다면 view independent color이기 때문에 원하는 바를 표현할 수 없었는데, SH coefficient를 부여하는 방식을 취하면 문제를 해결할 수 있다.
SH coefficient 값을 알고 있을 경우, basis function과 조합해서 다양한 (θ,ϕ)가 주어졌을 때 색상을 계산해낼 수 있기 때문이다. 똑같이 정해진 개수의 값을 들고 있지만 view depedent color를 표현할 수 있어서 활용되었다.
또 다른 예시는 3D gaussian splatting이다. 여기서도 공통된 3D gaussian을 갖고 다양한 시점에서의 view depedent color를 만들어내야 했기 때문에 단순 R,G,B 값을 추정하기 보다 SH coefficient를 추정했다.

'Knowledge > Vision' 카테고리의 다른 글
| Spherical gaussian 직관적으로 이해하기 (0) | 2023.12.21 |
|---|---|
| 3D transformation(R, t) matrix usage (0) | 2023.12.06 |
| Static library와 dynamic library 차이 (0) | 2023.09.14 |
| Positional embedding (직관적 이해) (0) | 2023.09.13 |
| Image flickering (0) | 2023.08.17 |