반응형
내 맘대로 Introduction
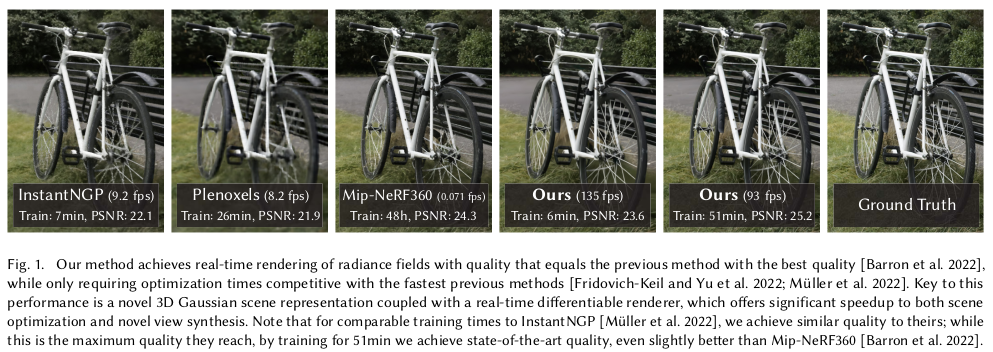
또 하나의 역대급 논문이 나온 것 같다. NeRF가 씹어먹고 있던 view synthesis 흐름에 새로운 컨셉이 등장했는데 NeRF를 압도하는 존재감을 바로 보인 논문이다. 2023년 SIGGRAPH에 등장한 논문인데 공개 2달 만에 6.6k star가 넘었다. (2023.10월 말 기준)
NeRF는 공간 전체에 대해 색상과 불투명도를 예측하는 implicit function을 학습시키는 것이라면 이 논문은 다시 explicit으로 돌아간 논문이다. 비유하자면 복원할 공간에 (색상, 불투명도, 크기, 방향)을 가진 무수히 많은 쌀알들을 채워넣는 컨셉이다. 공간 자체에 구석구석 쌀알들로 채워놓으면 나중에 rendering을 하고자 할 때 쌀알들을 갖고 색상을 칠해버리면 끝이다.
explicit하게 존재하다 보니 rendering을 위해 미리 계산해둘 수 있는 부분들이 늘어나고, 공간 내 불필요한 영역까지 커버할 필요가 없어지므로 속도 이점이 엄청나게 큰데 성능까지 압도해버린다. 특히 noise가 적다.
비유를 쌀알로 했지만 3D gaussian을 활용한 방법이고 공간을 3d gaussian으로 채우는 방법 (SfM으로 초기 위치 잡고, 증식하고 소멸하는 방식)과 이를 완성했을 때 rendering을 빠르게 하는 방법까지 소개한다. 후자는 vision 영역을 넘어가므로 자세히 이해하지 못했다.

메모하며 읽기
 |
|
 |
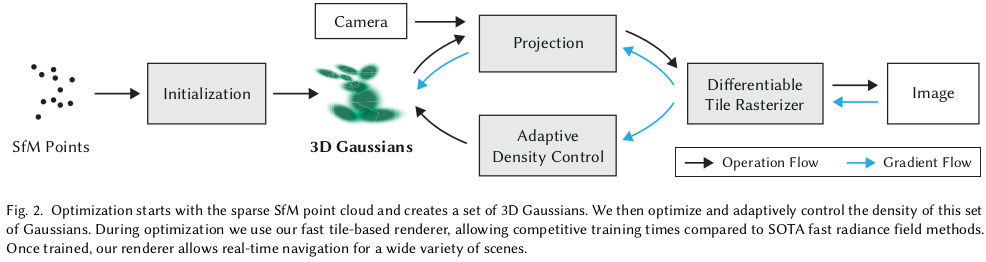
크게 initialization, adaptive density control, projection, tile rasterization 4단계로 나뉜다. 1) intialization SfM 돌려서 얻은 3d point 위치에 3D gaussian(position, color, covariance, opacity)을 할당함 2) adaptive density control 형상을 커버하기 위해 3D gaussian 개수가 더 필요한지, 아님 줄어들어야 하는지 판단해서 증식하거나 소멸함 3) projection rendering을 위해 3D gaussian을 2D pixel level gaussian으로 projection하는 수식이 필요함 4) tile rasterization projected 2d gaussian을 갖고 이미지를 렌더링함 --- 1) initialization은 사실 내용보단 구현이 중요한 거라서 코드를 보는게 나음. |
  |
일단 3D gaussian은 정의하긴 쉽다. 그냥 position, SH coefficients, opacity, scale을 부여하면 정의되는 확률 분포니까 말이다. 수식(4)와 같이 언제든 값으로 반환할 수 있으니 정의만 하면 됨. 중요한 것은 수식(5)와 같이 2차원으로 내려찍는 과정이다. 3D gaussian은 projection한다면 2D gaussian으로 될 것임은 분명하기에 mean은 proeject(position) 하면 되고 variacne에 해당하는 것만 잘 projection해서 2차원 variance로 바꿔주면 된다. 이 과정도 사실 간단하다. Cov(x)를 알고 있을 때 Cov(Ax)는 ACov(x)A.T 라는 것은 밝혀진 사실이니 여기에 matrix A를 projection matrix P를 넣어주면 되는 것이다. P = K[R|t] = KT 라고 할 수 있는데 notation만 T를 W로 바꿔주면 수식(5)에 근접해진다. var2d = (K)(W)var3d (W.T) (K.T) 여기서 종료하면 그만이지만 , 여기서 K 를 cam to img projection K[ I | 0] 으로 바라보면 non-linear한 부분이 있다. (homogeneous coord.를 쓰므로 linearize된게 맞긴 한데 공간과 pixel 간의 대응 관계를 보면 non-linear한게 맞다.) 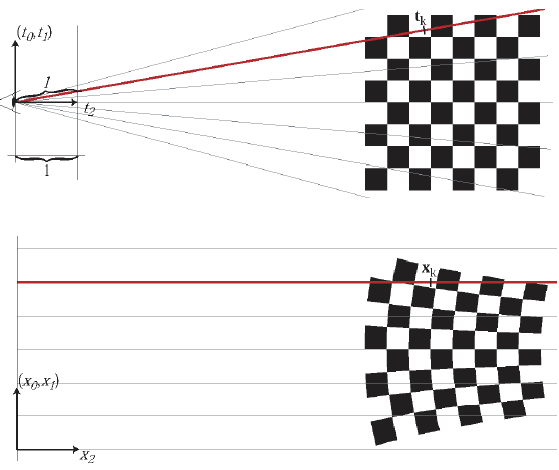 무슨 소리냐면, 대충 위 그림에서 보면 pixel 하나가 담고 있는 공간 정보를 보면 고르지 않다는 것을 볼 수 있다. 직관적으로 보면 3d guassian을 K로 표현된 수식으로 만약 projection한다면 2d gaussian이 되는 것은 맞지만 실제 3차원 공간 상의 3d gaussian 과는 약간의 갭(왜곡)이 있다는 것이다. 따라서 linearize를 한 번 해줘서 이런 효과를 무뎌지게 해줄 필요가 있었다. K[I|0]을 taylor series expansion한 다음 1st order term에서 절삭해내는 식으로 말이다. 그러면 K = M + J *M'과 같이 표현될 수 있는데 이걸 대입해서 다시 전개해보면 Covariance 계산 과정에서는 J만 살아남아 수식(5)와 같이 되는 것이다. ------------ 추가적으로 3d gaussian의 sigma는 scale값을 직접 추정해서 찾도록 할 수도 있는데 이러면 수렴 과정에서 scale이 음수가 되버리는 경우가 있을 수 있다. covariance가 PSD matrix일 때만 물리적으로 의미를 갖는 과정에서 이러한 문제는 악영향을 줄 수 있다. 또한 symmetric 한 특성을 유지하도록 바로 설계하는 것은 더 어려울 수 있다. 따라서 Cov(x) = SS.T와 같이 자기 자신이 곱해지도록 설계해서 사용했다. 이러면 항상 양수임과 동시에 SYMMETRIC이 무조건 유지되기 때문이다. 여기에 3D gaussian이 회전하는 R를 곱해준다면 Cov(Rx) = RSS.T R.T가 되는 것이다. |
 |
이렇게 3D gaussian으로 표현하려고 시도하는 것 자체가 효과적인가를 한 번 짚어주고 논문을 전개하는데, 옆에 그림은 학습 완료된 3D gaussian의 scale을 임의로 줄여 그 표현력을 줄인 것 예시인데 60% 까지 둘였음에도 형상을 유지하고 어느정도 비슷한 표현을 해내는 것을 볼 수 있다. 따라서 3D gaussian을 이용한 view synthesis가 가치있는 접근법이라고 보여준다. |
  |
이제는 3D gaussian을 형상에 맞는 개수로 늘리거나 줄이는 컨트롤에 관한 부분이다. 필요 이상으로 너무 많다면 연산량 + 렌더링 시간이 늘어나고, 너무 적다면 렌더링 퀄리티가 떨어질테니 여러모로 적정 개수를 유지하는 것이 좋다. 작은 쌀알 여러개로 채우는게 유리한 공간이 있다. 큰 쌀알 몇개로 채우는게 유리한 공간이 있을 수 있으니 직관적으로도 컨트롤을 해줘야 할 것 간다. 개수가 확정를 확정하는 동시에 학습을 계속 진행되는데 NeRF와 같이 최종적으로 color l1 loss와 d-ssim loss를 사용했다고 한다. |
  |
 3d gaussian 개수 컨트롤 방법을 그림으로 보는게 빠르다. 첫번째 그림처럼 공간 대비 현재 3d gaussian이 너무 작은 경우 분열하도록 했다. 분열하는 기준은 첫 3d gaussian이 backward 과정에서 받는 position gradient 크기를 보고 결정했다. 이 gradient의 크기가 0.0002 이상이 되면 해당 방향에 똑같은 크기의 3d gaussian을 하나 더 생성한다. 반대로 두번째 그림처럼 공간 대비 현재 3d gaussian이 너무 크면 gradient 방향으로 크기를 1.6배 줄인 하나를 더 생성하고 원래 것도 1.6배 축소한다. 즉 분열하는 것이다. 이러한 식으로 100 iteration마다 반복하면서 개수를 늘린다. 그럼 없애는 것은 어떻게 하느냐? 매 3000 iteration마다 현재 생성된 3d gaussian의 opacity를 임의로 전부 0으로 초기화한다. 그러고 다시 학습을 진행시키면 진짜 유의미한 3d gaussian만 공격적으로 원상복구되고 나머지는 도태된다고 한다. 그러면 이 도태된 애들만 적정 값으로 필터링해주면 된다. |
  |
여긴 그래픽스 영역으로 넘어가는 것이라서 직관적으로 밖에 이해 못했다. 렌더링하는 과정인데, 3d gaussian이 학습 완료되었다면 렌더링할 때 이미지를 16x16로 다 쪼갠다. (병렬처리할 때 하나의 단위가 된다.) 그런다음 각 tile마다 view frustrum culling을 해서 tile에 projection될 수 있는 3d gaussian을 추리고 그 position을 이용하여 누가 앞에 있는지 뒤에있는지 sorting해둔다. 이후 맨 앞 3d gaussian 부터 color+opacity를 이용해 색상을 채워나가고 opacity 누적값이 1에 근접하면 멈추는 식으로 렌더링을 한다. sorting index를 이미 들고 있기 때문에 굉장히 간단하게 칠할 수 있다. ---- 이렇게 CUDA코딩으로 렌더링을 병렬처리해서 구현하는 과정을 통해서 pytorch gradient와의 단절이 발생하는데 gradient는 손수 계산해서 연결해줬다. (supplementary에 보면 나옴) 그렇게 연결하고 l1 + d-ssim으로 학습시키면 됨. |
   |
학습이 마냥 간단하진 않아서 저해상도에서 250~500 번 정도 먼저 돌려주고 본학습을 시작했고 SH도 약간의 트릭을 사용해줬다.(뭔지 이해 못함) |
 |
  |
 |
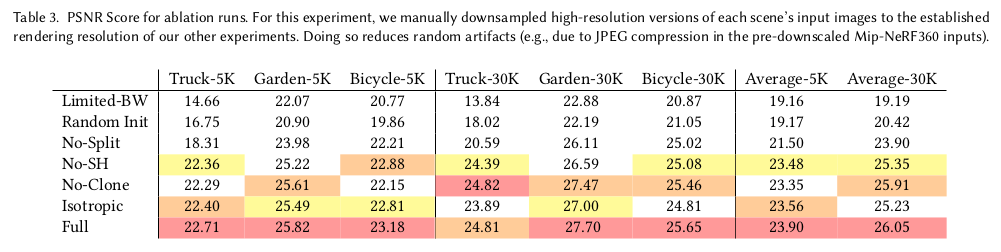
 SfM 초기값 없이 하면 완전 망하냐라고 궁금했는데 완전 망하진 않고 배경에서 조금 성능이 떨어진다고 함. sfm 보면 배경에서 매칭이 많이 되니까 그런듯? 먼 공간, 이미지에 덜 노출되는 공간은 sfm이 잡아주는게 큰 듯함. |
 |
  |
 |
Reference
반응형
'Paper > Neural rendering' 카테고리의 다른 글
| Deformable 3D Gaussians for High-Fidelity Monocular Dynamic Scene Reconstruction (0) | 2023.11.14 |
|---|---|
| 4D Gaussian Splatting for Real-Time Dynamic Scene Rendering (0) | 2023.11.03 |
| NeRF−−: Neural Radiance Fields Without Known Camera Parameters (0) | 2023.10.30 |
| BARF : Bundle-Adjusting Neural Radiance Fields (0) | 2023.10.30 |
| Self-Calibrating Neural Radiance Fields (0) | 2023.10.30 |