반응형
내 맘대로 Introduction

제목에서도 심플함이 느껴지는데 point cloud registration을 잘하는 논문이다. 딥러닝을 쓰지도 않았고 복잡한 개념도 없이, 정합을 위해 집중해야하는 영역들을 잘 추려내는 것에 집중해서 성능을 끌어올렸다. 아이디어가 심플함에도 성능 향상이 커서 CVPR 2023 student best paper를 수상한 논문이다. 대단..
핵심은 maximum clique (graph theory에서 나옴)로 추린 점들을 비교했었는데 maximal clique로 추린 점들을 비교한 것이다.
메모하며 읽기
 |
일단 maximum과 maximal의 차이를 알아야한다. (나도 처음 알았다...) --- An element is a maximum if it is larger than every single element in the set, whereas an element is maximal if it is not smaller than any other element in the set --- 수학적 정의는 위와 같은데, 일반적인 {a, b, c, d ..}와 같은 집합을 생각하면 maximal == maximum인 경우 뿐이라 차이를 이해하기 쉽지 않다. 다른 말로 웬만해서는 서로 같단 소리. 둘의 차이는 partially ordered set일 때 드러나는 것인데 preorder set, partially ordered set 이런 것들은 order theory까지 가는 먼길 이라 포기하는게 낫다. 직관적으로 이해하자면, maximum은 모든 것 중에 최상급이고 maximal은 주어진 상태에서 최상급이라고 이해하면 편하다. |
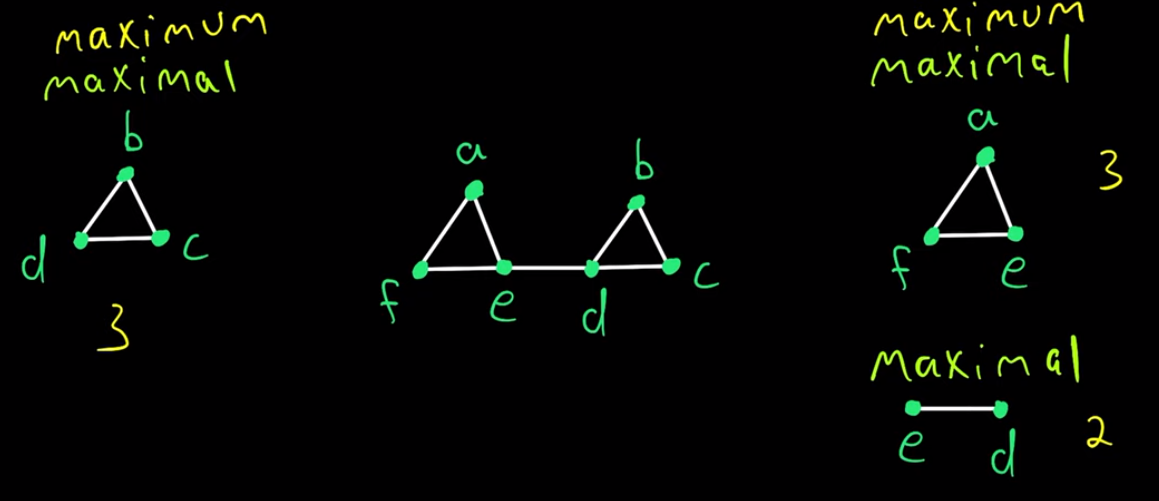 |
위 maximal와 maximum의 직관적 이해만 가지고 graph theory로 넘어오면 maximal clique와 maximum clique가 존재한다. 먼저 clique란 graph에서 모든 node가 서로 인접한 상태를 유지하는 고리 같은 개념이다. 옆 그림에서 bcd, ed, aef 같은 것이 clique다. maximal clique란 주어진 node로 보았을 때 더 새로운 node를 추가할 수 없을 때까지 확장한 최대 clique이다. 다른 말로 ed를 보면 a,b,c,f 중 어떤 node를 추가하더라도 모든 node가 서로 인접한 상태를 만들 수 없으므로 ed가 지금 주어진 상황에서 최대 상태다. 따라서 ed 는 maximal clique이다. maximum clique는 전체에서 최상급이기 때문에 maximal clique 중에서도 크기가 가장 큰 clique를 말한다. 옆 그림에서는 bcd와 aef가 크기가 3이므로 maximum clique가 된다. num(maximal cliques) << num(maximum cliques) 가 되는 것이다. |
 |
|
  |
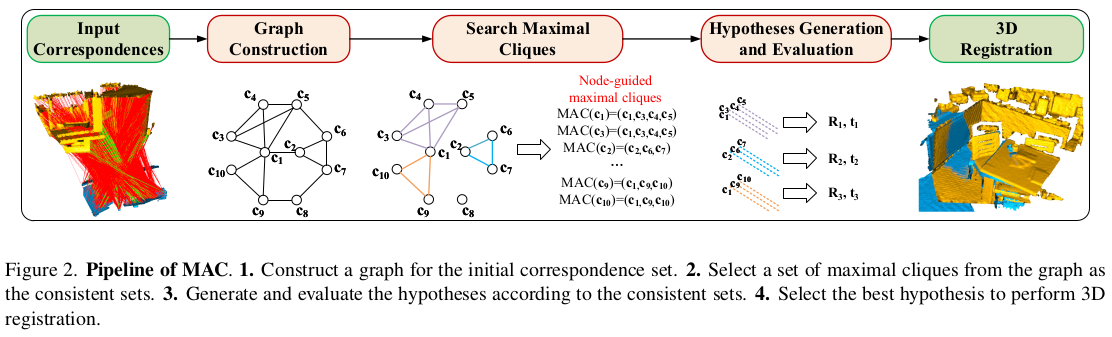
1) 어떤 방식으로든 point feature or descriptor를 뽑아두었다는 전제 2) feature (or descrptor) matching을 통해 initial correspondence 생성 3) maximal clique 후보군들 생성 + 필터링 (개수 줄이기) 4) RANSAC 돌면서 가장 좋은 결과 선정. |
  |
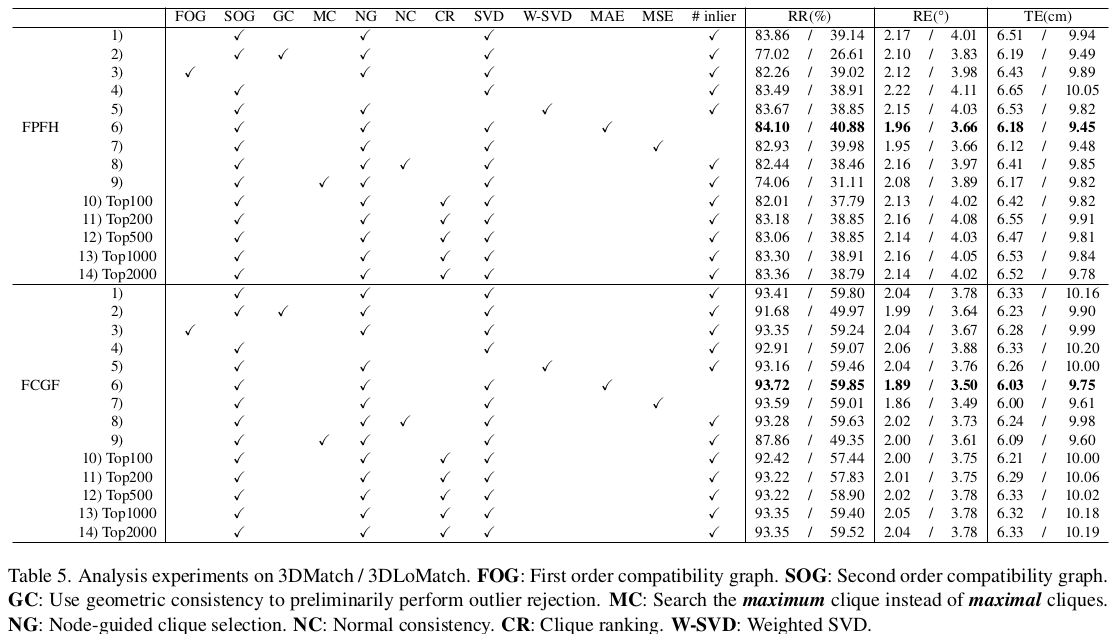
graph에서 node는 correspondence, edge는 correspondence 간 compatiblity (상호호환성이지만 그냥 끼리끼리 묶을만한 관계라는 뜻) 을 의미한다. correspondence는 feature matching으로 만들어 두었고, edge를 사이에 놓을 것이냐 말 것이냐는 weight를 계산해서 결정한다. 총 2가지 weight 계산 방법이 있는데 첫번째는 단순히 correspondence 간의 거리가 source, target point cloud에서 일정 거리 안으로 동일할 경우, 충분히 끼리끼리 묶을만하다고 판단하는 방식이다. 수식(1)과 같이 간단히 거리 오차를 평가하고 이를 gaussian으로 표현함으로써 weight 화 한다. FOG 라고 하며 이는 symmetric matrix로 나온다. 두번쨰로 SOG라고 불리는 앤데, 그냥 FOG를 곱하고 곱한 것이다. 원리야 논문 [8]번에 나와있겠지만 직관적으로 보았을 때 weight 중 1에 가까운 애들은 곱하고 곱하는 과정에서 강조되고, 0에 가까운 애들은 곱하고 곱하는 과정에서 도태될 것이므로 집중할 edge만 남는 weight라고 보면 되겠다. 이 두 가지 weight의 threshold를 hyper parameter로 두고 graph를 형성한다. |
 |
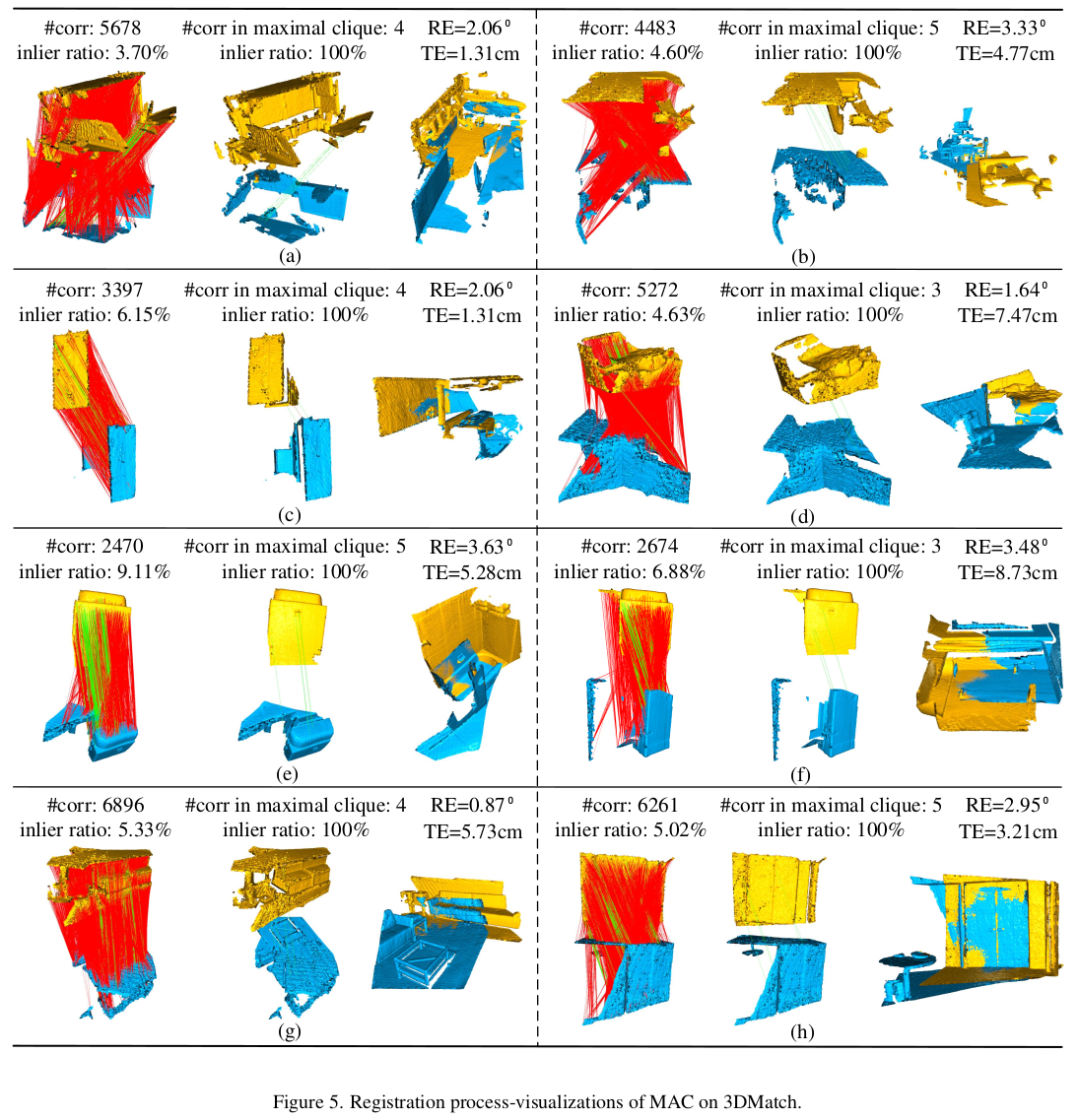
생성한 weight로 만든 graph를 갖고 maximal clique들을 추려내는 단계다. 기존 논문들에서는 maximum clique를 사용했다는데 maximal이라는 점에 주목해야 한다. library가 제공되는 걸 사용했다고 한다. |
  |
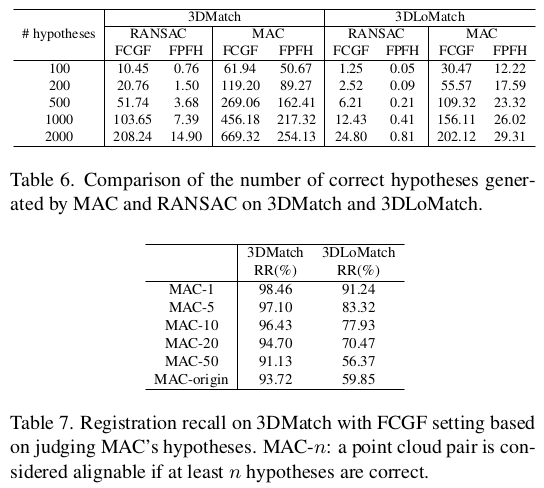
MAC를 생성해보면 vertex 수보다 더 크게 나오기도 하는데 이러면 너무 느려진다. 따라서 필터링이 필요했다. 필터링을 하는 방법은 SOG로 만든 weight로 판별하는 방법이다. node가 포함된 MAC 중 가장 weight가 높은 MAC만 추려냄으로써 MAC 개수가 vertex 개수를 넘지 않도록 억제했다. 추가적으로 normal을 이용해서 edge마다 normal이 일치하는지 보고 일치하는 MAC들만 살려냈으며 SOG weight 로 sorting 해서 hyper parameter N개로 잘라내어 개수 조절을 했다. |
  |
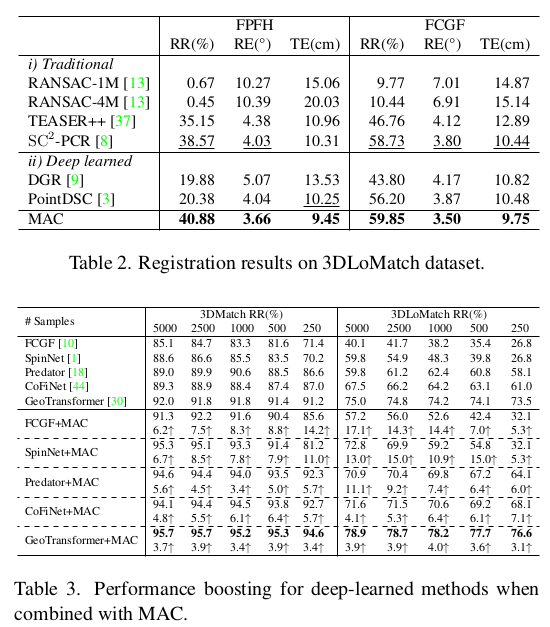
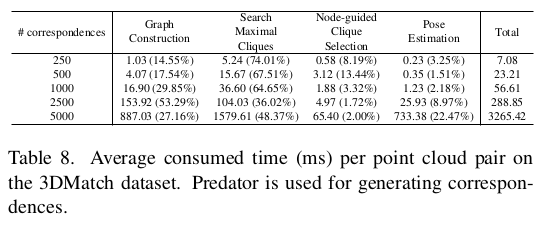
이후에는 MAC 마다 한 번씩 iteration을 돌면서 가장 error가 적은 MAC를 찾는 과정을 반복한다. argmax이다. error는 SVD로 찾는 것이 일반적이므로 그대로 사용했고 weight가 주어진 상황이므로 weighted SVD도 선택할 수 있도록 했다. RANSAC을 돈다. |
 |
 |
  |
 |
 |
 |
반응형