*34강은 시험 해설 강의로 생략한다.
Lecture
Lecture 33: Left and right inverses; pseudoinverse | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note

- 우리가 흔히 아는 inverse는 어느 쪽에 곱해도 identity가 된다.
- 이것은 A가 square matrix이면서 full rank일 때만 성립하는 이야기다.
- 그러면 만약 A가 rectangular matrix이고 full rank가 아니면 어떻게 될까? 그것이 left inverse, right inverse, pseudo inverse의 시작이다.

- 먼저 left inverse는 A 가 m x n matrix일 때 m > n (overdetermined), full rank일 때의 inverse이다.
- A가 full column rank이기 때문에 A.T A 가 positive definite이면서 invertible하다는 것을 알기 때문에 이를 조합해서 위와 같이 만들 수 있다.
- rectangular matrix이기 때문에 inverse가 안되는 것이 맞지만 m>n, full column rank라는 특징을 이용해 억지로 왼쪽에 곱해졌을 때 identity가 나오는 matrix를 만들어낸 것이다. 이를 left inverse라고 부른다.

- right inverse도 마찬가지다. A가 m x n matrix일 때 m < n (underdetermined), full rank일 때의 inverse이다.
- A가 full row rank이기 때문에 A A.T 가 positive definite이면서 invertible하다는 것을 알기 때문에 이를 조합해서 위와 같이 만들 수 있다.
- rectangular matrix이기 때문에 inverse가 안되는 것이 맞지만 m<n, full row rank라는 특징을 이용해 억지로 오른쪽에 곱해졌을 때 identity가 나오는 matrix를 만들어낸 것이다. 이를 right inverse라고 부른다.

- 마지막으로 pseudo inverse는 A가 m x n matrix 이고 full rank가 아닐 때의 inverse이다.
- 이것은 못 푸는게 맞다. 하지만 입력이 되는 x (in row space)가 Ax (in column space)로 mapping될 때, 1대1 대응이 성립한다는 성질을 전제로 "최대한" 2-side에 곱해졌을 때 identity에 가까운 결과를 내는 matrix를 찾는 것이다.
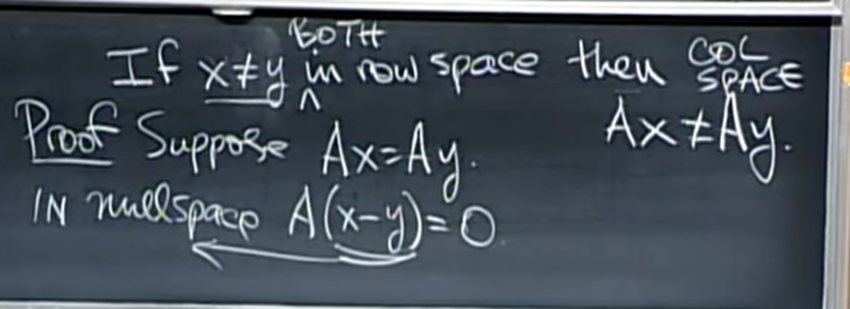
- x->Ax 는 1대1 대응이라는 것을 확실히 하기 위해 증명을 보면 위와 같다. row space에 있는 다른 벡터 x, y가 만약 같은 값으로 mapping된다고 하면 A(x-y)=0을 만족해야 한다.
- 하지만 이 때의 해는 x=y (조건 모순) 이거나 x-y 가 null space여야 한다. 후자 역시 x, y가 row space 벡터이면 x-y도 row space 벡터이므로 모순이다. 따라서 x->Ax mapping을 1대1 대응이다.

- 구하는 방법은 SVD에서 시작한다. USV.T로 분해가 되는 SVD 형태에서 A가 full rank가 아니더라도 V와 U는 invertible한 것은 안다. 게다가 orthonormal 하기 때문에 transpose가 inverse다.
- 그 상황에서 S+ 를 어떻게 정의해야 가장 identity에 가까워질지 값을 맞추고 재조립하면 pseudo inverse가 된다.
- S는 대각 성분에 eigenvalue가 차있는 matrix이지만 현재 m != n 이고 full rank도 아니기 때문에 m x n matirx 이면서 rank 개수까지만 대각 성분이 차있고 나머지는 0으로 차있는 형태다.
- S의 앞 뒤로 곱해졌을 때 대각 성분을 1로 만들어 그나마 identity에 가깝게 만들어 주는 matrix S+는 위 칠판과 같이 n x m 형태의 대각 성분이 역수가 취해진 matrix다.
- 결과적으로 A+ = V S+ U.T로 구해진다.

- 알고 있으면 좋은 내용은, A A+ 는 m x m matrix로써 column space로 projection하는 matrix이고 A+ A는 n x n matrix로써 row space로 projection하는 matrix다.
- 위 사진을 보면 left inverse를 오른쪽에 곱하고, right inverse를 왼쪽에 곱하면 각각 앞선 강의에서 배운 projection matrix 형태를 띄고 있는 것을 알 수 있다.
- 이것은 identity로는 못가지만 반대 방향에서도 identity로 "최대한" 만들려고 하는 역할을 수행한다는 것이다.
- 다시 돌아와 pseudo inverse에 대입해보면, 2-side 모두에서 identity를 "최대한" 만들려고 하는 projection matrix의 역할을 수행한다고 해석할 수 있다. 근데 그 projection 대상이 되는 space가 방향에 따라 column space냐 row space냐의 차이가 있다.
Conclusion
용기 내서 다시 공부하기 시작한 것이 1월 3일인데 거의 1달 하고도 1주일의 시간이 걸렸다. 체감으로는 꽤나 오래 걸린 것 같은데 대학생 때 한 학기에 걸쳐 배운 내용을 1달만에 배운 것이라고 생각하니 나름 괜찮게 끝낸 것 같다.
선형대수를 다시 보기로 각오한 이유가 기본기를 다지기 위함이었는데 그 목적에 충실할 정도로는 이해를 한 것 같아 전반적으로 만족한다. 특히 A.T A가 왜 그렇게 주구장창 등장하는지 이해할 수가 없었는데 이제 완벽히 이해해서 더 이상 헷갈릴 일은 없는 것 같다.
듣는 내내 칠판을 보면서 공부하다보니 약간의 학생된 느낌을 다시 느낄 수 있어 좋았고 강의 하나 하나 쌓아나갈 때 느껴지는 뿌듯함이 직장 생활을 하면서 부족한 하루의 보람을 잘 채워준 듯 하다. 지식 외적으로도 느낀 것이 많은 시간이었다. 다른 공부할 거리를 계속 찾아 이렇게 꾸준히 강의를 듣는 것도 참 좋을 것 같았다.
선형대수 끝!
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 31-32. Change of basis; image compression (0) | 2023.02.10 |
|---|---|
| [Linear algebra] 30. Linear transformations and their matrices (0) | 2023.02.09 |
| [Linear algebra] 29. Singular value decomposition (0) | 2023.02.08 |
| [Linear algebra] 28. Similar matrices and Jordan form (0) | 2023.02.04 |
| [Linear algebra] 27. Positive definite matrices and minima (0) | 2023.02.04 |