반응형
Lecture
Lecture 28: Similar matrices and Jordan form | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note
- 지난 강의에서 배운 positive definite matrix를 조금 더 다루고 similar matrix 개념으로 넘어간다.

- positive definite matrix는 sum에 닫혀있다. A와 B가 각각 positive definite matrix라면 A+B도 필연적으로 positive definite이다.
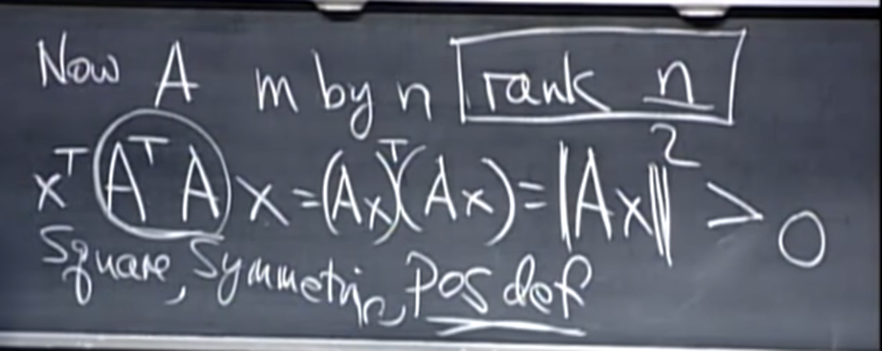
- A가 overdetermined matrix(세로로 긴 rectangular matrix)일 때 이를 분석하는 과정에서 A.T A가 자주 등장한다.
- A.T A는 positive definite test 4번째에 따라 x.T A.T A x 로 풀어보면 위 사진과 같이 ||Ax|| 가 된다는 것을 알 수 있다.
- 따라서 이는 최소 0이거나 양수이다.
- 만약 rank가 full rank n일 경우, null space가 zero vector 뿐이므로 x가 0인 경우를 빼고는 모두 양수라고 보장할 수 있다.
- 따라서 full rank overdetermined matrix면 A.T A는 무조건 positive definite이다.
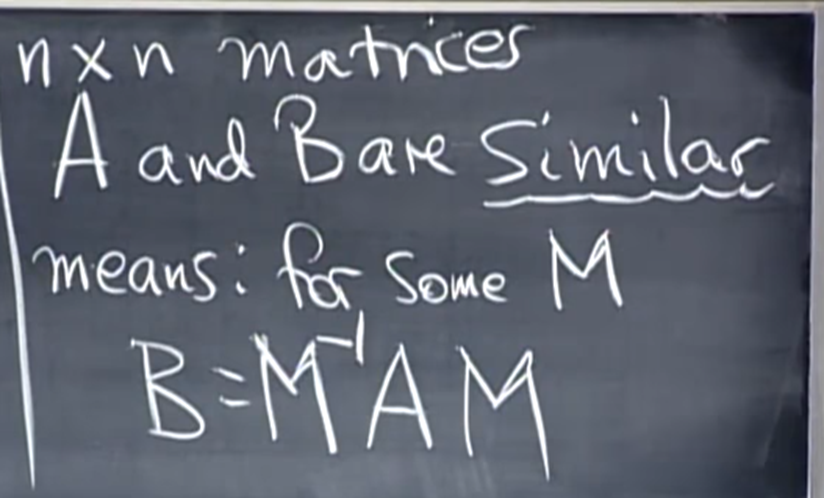
- similar matrix란 위와 같이 임의의 M matrix를 앞뒤로 곱했을 때 나오는 모든 matirx B를 의미한다.
- 다른 말로 특정 M을 찾아낼 수 있다면 A와 B는 similar하다고 볼 수 있다.
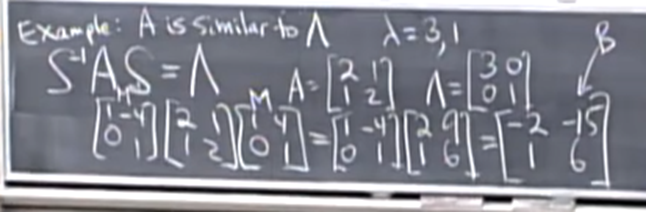
- 예를 들어, 앞서 배운 eigenvector matrix와 eigenvalue matrix로 decomposition하는 수식도 similar matrix의 한 형태임을 볼 수 있는데 이 경우 A와 eigenvalue matrix가 similar하다고 할 수 있다.
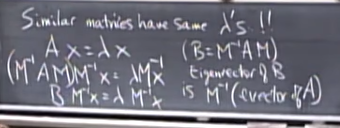
- similar matrix 개념의 핵심은 eigenvalue가 동일한 matrix라는 것이다. 증명은 위 사진과 같다.
- 단, eigenvalue 만 동일할 뿐 eigenvector는 M inverse가 곱해진 형태로 값이 다르다.

- similar matrix 개념을 다룰 때 안 좋은 matrix 형태들이 있는데 그것은 eigenvalue가 중복될 때다.
- 일단 eigenvalue로만 이루어진 diagonal matrix일 경우, similar matrix가 없다. 자기 자신 뿐이다. 따라서 활용이 안된다.
- 두번째로 eigenvalue 로만 이루어진 diagonal matrix는 아니지만 애매하게 값이 upper triangle 위치에 차있어서 diagonalize는 안되는 경우다. 1로 차있는 형태를 Jordan form이라고 한다.
- (Jordan form이면 왜 similar matrix 개념 상 bad case인지 설명 안해준다... 이해 못하겠음)

- Jordan form의 예시는 위와 같다. eigenvalue는 중복되고 upper triangle 위치에 1이 조금씩 차있는 형태다.
- 참고로 1이 차있으므로 rank가 몇 개 생기는데 rank 개수만큼 eigenvector가 생길 것이다. 이 때 각 eigenvector를 만들어내는 핵심 위치(대각성분에 걸친 위치)들을 block으로 나눌 수 있는데 이걸 jordan block이라고 한다.
- eigenvalue가 중복되어 있을 때 jordan block의 사이즈가 다르면 둘은 similar하지 않다고 한다.
- (그냥 Jordan form이라는게 있다 라고 뜬금없이 알려주는 강의라서 깊게 이해할 순 없는 것 같다. Jordan matrix의 활용, 계산, 의미 등은 스킵한 채 예시만 보여주고 넘어간다. 따라서 파고 들어 이해할 만큼 크게 중요하지 않은 듯?)
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 30. Linear transformations and their matrices (0) | 2023.02.09 |
|---|---|
| [Linear algebra] 29. Singular value decomposition (0) | 2023.02.08 |
| [Linear algebra] 27. Positive definite matrices and minima (0) | 2023.02.04 |
| [Linear algebra] 26. Complex matrices; fast fourier transform (0) | 2023.02.02 |
| [Linear algebra] 25. Symmetric matrices and positive definiteness (0) | 2023.02.02 |