반응형
*32강은 퀴즈 해설 강의로 생략함.
Lecture
Lecture 31: Change of basis; image compression | Linear Algebra | Mathematics | MIT OpenCourseWare
MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity
ocw.mit.edu
Note
- linear algegra가 쓰이는 대표적인 부분 중 하나는 이미지 압축이다.
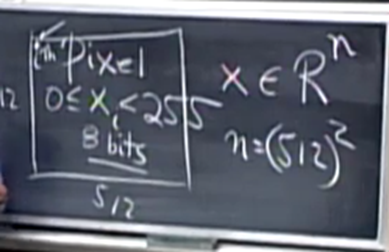
- 이미지가 주어졌을 때 모든 픽셀을 flatten 해서 R^n vector로 표현하고, 이를 basis의 linear combination으로 표현하는 방식이다.
- 원본 이미지 자체는 n^2* 8bit (gray scale이 아니라면 3배 더) 의 메모리가 필요한데 이를 basis의 조합으로 표현할 시 m * n * 8 bit면 충분할 것이다.

- 좌측 같이 standard basis를 사용한다고 하면 m ~= n이기 때문에 큰 의미가 없을 것이다. 하지만 우측과 같이 이미지의 특성을 조금 반영해서 전체 흰색, 절반 흰색+절반 검은색, 흰색/검은색 반복처럼 색 표현에 특화된 basis를 이용하면 압축율이 커진다.
- 따라서 어떤 basis를 선택하느냐가 중요하고, 새로운 basis를 찾으면 해당 basis로 바꾸는 방법도 중요하다.

- 이미지에서 가장 효과적인 basis는 fourier basis다. 좌측에 보이는 것과 같이 fourier series에서 사용되는 vector를 basis로 사용하고 n=64으로 한다. 이미지도 이에 맞추기 위해 8x8로 쪼개는 트릭을 같이 써서 극대화 한다.
- 압축 과정은 첫번째로 basis의 계수를 구하는 것이다. 그리고 두번째로 계수 중 값이 일정 기준 이하일 경우 버리는 것이다. 이렇게 되면 남아있는 계수와 그 대응되는 basis만으로 최소 손실로 이미지를 압축할 수 있게 된다.
- 하나 더 fourier basis가 좋은 점은 몇몇 개수가 버려진다고 하더라도 남은 basis들이 표현력이 충분해서 손실율이 훨씬 적다는 것이다.

- wavelets basis는 fourier basis와 맞먹을 정도로 간단하고도 파워풀한 basis인데 FBI 가 finger print 이미지를 압축할 때 사용한다고도 한다.

- basis를 변경하는 것도 간단하다. w라는 basis에서 p라는 basis로 변경하고 싶으면 단순하게 p를 표현하기 위한 w basis의 계수를 찾으면 된다. 좌측 사진과 같다.
- 이렇게 되면 p=wc라는 수식을 만족하는데 여기서 w가 basis matrix 이므로 invertible하고 그냥 풀면 끝이다.
- 이 과정에서 inverse가 들어가기 때문에 좋은 basis라고 하는 조건 중 하나 쉽게 inverse가 가능해야 한다. 예를 들어 orthonormal basis여서 transpose만으로 inverse를 구할 수 있으면 좋은 basis다.

- new basis를 모를 때도 변경할 수 있다. 가령 transformation matrix T와 old basis x는 아는데 새로운 basis w를 찾고 싶은 경우다.
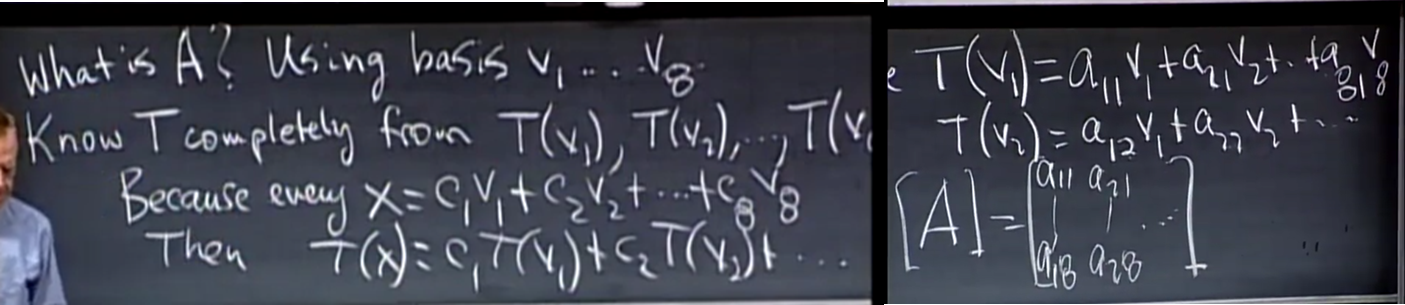
- 그럴 땐 위와 같이 T가 linear transform이라는 것을 이용해서 위와 같이 풀면 된다. x=c1v1+c2v2+...+c8v8이면 T(x)=c1T(v1)+c2T(v2)+...c8T(v8) 이라는 것을 알고 있으니 간단하게 계수를 찾을 수 있다.

- 참고로 old basis matrix와 new basis matrix는 similar matrix 관계에서 서로 변환된다.

- 위 계산 과정에서 느꼈다면 알겠지만, 계수를 찾을 때 복잡하게 여러 계수가 등장하지 않는 경우가 있는데 바로 basis가 eigenvector일 때다.
- 이 경우, 계수가 1개만 존재한다. 바로 eigenvalue로.
- 결론적으로 모든 basis 중에 가장 좋은 것은 eigenvector다. 하지만 이미지 압축과 같이 eigenvector를 찾는 연산이 오히려 전체 연산량을 늘릴 경우에는 fourier나 wavelets 같은 사전 정의된 basis를 쓰는 것이다.
반응형
'Knowledge > Linear algebra' 카테고리의 다른 글
| [Linear algebra] 33-34. Left and right inverses; pseudoinverse (0) | 2023.02.10 |
|---|---|
| [Linear algebra] 30. Linear transformations and their matrices (0) | 2023.02.09 |
| [Linear algebra] 29. Singular value decomposition (0) | 2023.02.08 |
| [Linear algebra] 28. Similar matrices and Jordan form (0) | 2023.02.04 |
| [Linear algebra] 27. Positive definite matrices and minima (0) | 2023.02.04 |