반응형
내 맘대로 Introduction
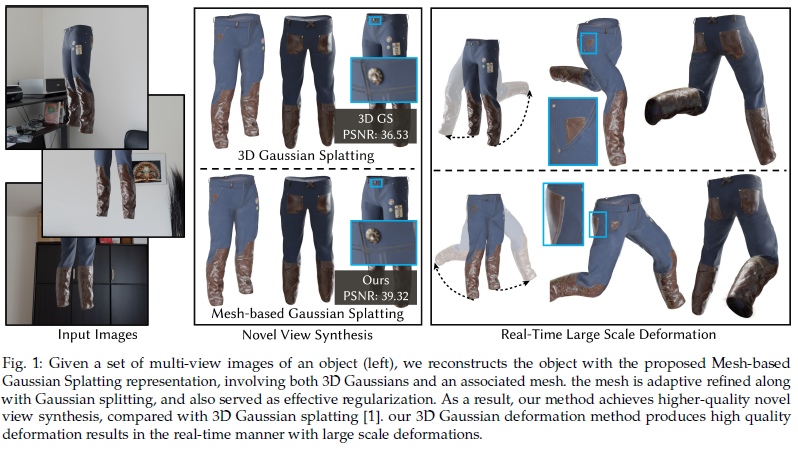
요즘 부쩍 mesh랑 3d gaussian을 엮으려는 시도가 많은 것 같다. 3d gaussian splatting이 기존 graphics tool에 그냥 갖다붙이기가 가능한 형태인 만큼 mesh랑 엮어서 세트로 가져갈 수 있게 하려는 것 같다.
이 논문은 3d gaussian들을 mesh face에 구속한 형태로 splatting해서 mesh deformation이 gaussian deformation을 직접 결정하게 하는 논문이다. mesh deformation은 control point를 이용하는 방법이든 손으로 하든 명확히 정의가 되어있으므로, 여기에 얹기만 하면 3d gaussian도 자연스럽게 deformation이 가능해진다는 논리다.
핵심 아이디어는 3d gaussian의 position을 face 안에서만 머물도록 하는 것 + face를 벗어나더라도 normal 방향으로만 벗어날 수 있도록 하는 것이다.
메모하며 읽기
 |
  |
| 3d gaussian을 구속할 기준 mesh는 주어진 데이터를 활용해서 NeuS2를 돌려서 얻는다. 워낙 검증된 방법이기 때문에 효과적인 초기 mesh를 얻을 수 있을 것 같다. | 3d gs recap은 생략. |
 |
mesh deformation은 기존 control point를 이용하는 방식으로 SE3 transformation을 vertex 단위로 쉽게 얻을 수 있다. 수식(2)와 같이 계산된 SE3를 갖고 주변 neighbor vertex를 최대한 유사하게 움직이도록 최적화해주면 전체 mesh가 움직이는 모양이 된다. 여기서 얻은 SE3를 polar decompostion으로 rotation + shear로 나누면 그대로 3d gaussian rotation + scale에 적용할 matrix로 바꿀 수도 있어서 아주 손쉽게 3d gs까지 연결할 수 있다. |
  |
3d gs는 각 face 중심에 생성하는 식으로 초기화함. 그리고 face normal에 수평한 방향+ 수식한 방향으로만 densification될 수 있도록 했음. reduction은 원본 3dgs 그대로 특정 iteration마다 opacity 0으로 초기화하는 방식으로 커버함. |
 |
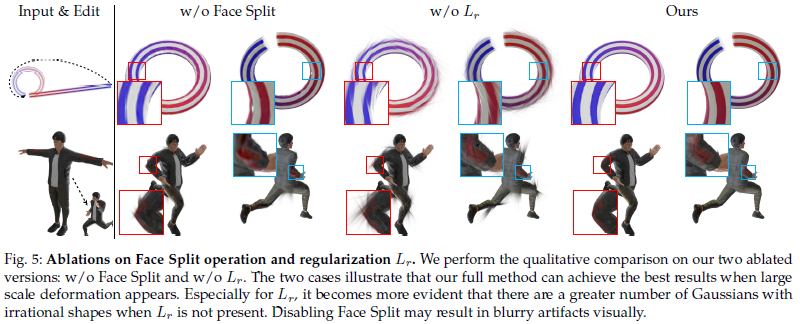
face normal에 수평한 방향으로 증식할 경우, barycenteric coordinate로 표현할 수 있으므로 수식(3)의 첫 괄호와 같이 간단히 적을 수 있고 수직하게 증식하는 경우 normal 방향 * 특정 scale로 표현할 수 있다. 참고로 R은 face를 둘러싸는 외접원의 반지름이다. 특정 scale을 찾을 때 열린 scale로 찾기보다 face 크기에 relative한 형태로 찾는 것이 찾기 쉬우니 이렇게 한 것 같다. -------- + 웬만하면 3d gaussian들이 face 크기를 넘어서지 않도록 억제한다. (불규칙하게 뾰족한 애들 생기지 않도록, 생기면 deformation했을 때 artifact 심해짐) |
  |
mesh deformation을 적용했을 때 vertex 별로 SE3를 쉽게 얻을 수 있다고 했다. 그리고 이를 polar decompostion하면 rotation, shear(scale)로 나눌 수 있다고도 했다. 수식(5)는 이렇게 찾은 rotation, shear를 앞서 정의한 barycentric으로 표현된 3d gs position들에 적용하는 과정이다. |
 |
color는 SH로 표현되어 있기 때문에 view-dependent 이므로, view direction에도 rotation을 곱해줘서 deformation을 반영할 수 있도록 해준다. |
  |
|
 |
 |
 |
 |
 |
반응형
