요즘 regression task를 풀고자 할 때 많이 시도하는 방법은 neural network를 이용하는 방법이다.
classification, detection 등등 온갖 주제에서 neural network가 regression에 폭발적인 성능을 보여준다는 것이 입증된지 오래여서, 가장 먼저 떠오르는 방법이 됐다. (요즘은 neural network를 쓰는 것이 computational cost 측면에서까지 좋을 때도 있다.)
하지만 Rotation 값을 regression하는 경우에는 약간 상황이 다르다.
Rotation은 유한한 범위 안에서 유일한 의미를 갖는 다른 값들과 달리, 범위가 무한하며 주기성이 있기 때문에 neural network를 이용하는데 어려움이 있다. (물론 풀긴 풀지만 성능이 아쉬운 때가 많다.)
직관적으로 다시 설명해보면, 데이터로부터 2차원 상의 어떤 각도 θ를 추정하는 상황이라고 해보자.
그렇다면 각도는 0~2π 값을 갖고 있으니, 단순히 network output으로 나오는 0~1 값에 2π를 곱해 network output이 각도에 1대1로 대응되도록 설계한 후 학습을 진행할 것이다. 사람의 직관으로는 전혀 문제가 없다.
하지만 0과 2π는 같은 값이다. 네트워크 입장에서는 양 극에 있는 가장 큰 차이가 있는 값으로 학습을 하지만 결국엔 같은 값이므로 네트워크가 제대로 학습할 수 없게 된다.
이와 같이 Rotation은 continuous space에 존재하는 값인데 neural network에 사용하기 위해 특정 representation space로 가져오는 순간, discontinous해지기 때문에 regression하기 어려운 대상이 돼버린다.
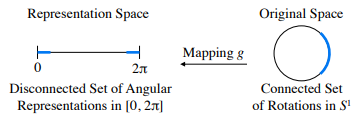
또한 수학적으로 가져야 하는 특징들도 계속 유지되어야 하기 때문에 더더욱 어렵다.
예를 들면, determinant가 항상 1이어야 하고, matrix 형태일 경우, transposed matrix가 inverse matrix이어야 한다는 특징들이 있다. 이것들은 네트워크에게 constraint로 제공할 수는 있겠지만 완벽하게 반영하기 꽤나 어렵다.
On the Continuity of Rotation Representations in Neural Networks
이 글에서는 위 문제를 지적하면서 아주 간단하면서도 나이스하게 풀어낸 논문과 그 내용을 간략 정리하려고 한다. 논문 링크는 하단에 걸어두었다.
논문에서는 rotation의 특징을 그대로 살릴 수 있는 continous representation space을 제시하면서 문제를 풀고자 한다.

예를 들면, 위 예시에서 0~2π를 그대로 추정하면 문제가 발생하는데 만일, angle을 cos과 sin으로 구성된 vector [ cos(θ), sin(θ) ]로 mapping하고 이를 네트워크가 추정하도록 하면 문제가 해결된다.
위 mapping된 vector는 주기성도 반영되어 있고, 유한한 값 -1~1이 정해져있으며, rotation이 갖추어야 할 특징도 그대로 유지된다.
위와 같은 경우, original space: θ -> representation space : [ cos(θ), sin(θ) ] 모두 continous하기 때문이다.
논문은 3차원 rotation에서도 위 2차원 예시처럼 continous representation이 존재한다며 그 방법을 소개한다.
혹자는 3차원도 그럼 위와 같이 cos, sin으로 구성된 matrix나 quaternion으로 표현하면 해결되는 것이 아니냐? 라고 할 수 있는데, 아니다.
왜냐하면 3D rotation을 조금 다루어본 사람이라면 누구나 알겠지만, 3차원은 2차원과 얘기가 다르다.
cos, sin으로 구성된 rotation matrix representation은 discontious하다. 이 형태도 결국엔 euler angle을 사용하는 것인데 3차원 회전을 연속적으로 표현할 수 없다. 증명까진 무의미하니 경험적으로 설명하자면, 종종 cos, sin 값은 찔끔 변했는데 헤까닥 축이 뒤집히면서 뱅글 돌아 움직이는 모습을 볼 수 있을 것이다. 이 현상의 원인이 euler angle로는 3차원 회전은 연속적으로 표현할 수 없기 때문이다. 또 짐벌락 같은 이슈도 있다.
quaternion을 써도 문제는 완전히 해결되지 않는다. 일단 quaternion은 norm 값이 1이라는 특징을 유지시키는 것이 일단 어렵고, quaternion은 180도 이상되는 각도를 표현할 수 없기 때문에 180도 이상을 표현하고 싶을 땐 축이 뒤집힌다. 그 말은 180도 회전의 경우, 2가지 선택지가 존재한다. 즉, discontinous한 부분이 있다.
따라서 새로운 방법이 필요하다고 할 수 있다.
Method
논문 내용을 하나하나 설명하기엔 Gram-Schmidt process 같은 것들의 증명이 필요하기 때문에 각설하고 방법만 기록하겠다. 아주 간단하다. (너무 좋다.)
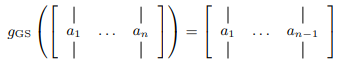
3x3 rotation matrix의 각 column vector 중 1번째와 2번째 column vector, 총 6개의 element로 rotation을 표현하면 된다.
즉, neural network 입장에서 1~2번째 column vector를 구성하는 6개의 값을 맞추도록 설계하면 된다. (증명은 논문 및 supplementary를 정독하길 추천)
의아할 것이지만 간단히 직관적으로 설명하면, 3번째 column vector는 1~2번째 column vector로 연산이 가능하기 때문에 1~2번째 column vector만으로 rotation을 표현해도 충분하다.
게다가 3번째 column vector를 계산하는 과정에서 섞이는 normalization 외 몇 step으로 rotation의 특징들이 강제로 유지되도록 한다. 연산 수식은 다음과 같다. (N : normalization, e: axis vectors 100 010 001)
그리고 1~2번째 column vector, 총 6개의 값으로 구성된 representation space는 continous하다.
network가 a1과 a2 (1~2번째 column vector)를 계산해 내었다면 다음 수식으로 b1, b2, b3를 계산한 뒤, [b1, b2, b3]으로 구성된 3x3 rotation matrix로 변형해서 사용하면 된다.

단번에 이해하는 사람이 없을테니 코드 예시를 보여주면,
import numpy as np
if __name__== '__main__':
## original rotation
R = np.array([[ 0.0333, 0.4427, -0.8960],
[ 0.9993, -0.0301, 0.0222],
[-0.0171, -0.8961, -0.4434]], dtype=np.float32)
## suppose these two vector are network outputs
a1 = R[:, 0] # first column
a2 = R[:, 1] # second column
## b1
a1_norm = np.linalg.norm(a1)
b1 = a1 / a1_norm
## b2
b2 = a2 - np.dot(b1, a2) * b1
b2_norm = np.linalg.norm(b2)
b2 = b2/b2_norm
## b3
e1 = np.array([1, 0, 0], dtype=np.float32)
e2 = np.array([0, 1, 0], dtype=np.float32)
e3 = np.array([0, 0, 1], dtype=np.float32)
b31 = np.linalg.det(np.concatenate([b1[:, None], b2[:, None], e1[:, None]], axis=1))
b32 = np.linalg.det(np.concatenate([b1[:, None], b2[:, None], e2[:, None]], axis=1))
b33 = np.linalg.det(np.concatenate([b1[:, None], b2[:, None], e3[:, None]], axis=1))
b3 = np.array([b31, b32, b33])
## reconstructed rotation
R_ = np.concatenate([b1[:,None], b2[:,None], b3[:,None]], axis=1)
print(np.matmul(R , R_.transpose(1,0)))
'''
This is an identity matrix, so R == R_
[[ 9.99954089e-01 1.66755060e-06 6.30064456e-06]
[ 5.85548718e-05 9.99999667e-01 4.22882117e-05]
[ 7.20003081e-06 -1.18633272e-06 9.99945588e-01]]
'''
# it is enough to represenate 3D rotation only with 6 values
a1, a2만으로 b1,b2, b3가 계산 가능한 형태라는 것을 알 수 있고, b1,b2,b3가 이루는 matrix는 a1, a2, a3가 이루는 matrix와 정확히 같다. a1, a2만 알면 모든 3D rotation을 표현할 수 있다. 심지어 continous하게.
따라서 실제로 사용할 땐 a1, a2를 네트워크가 맞추도록 한 뒤, 수식을 통해 3x3 rotation matrix로 변환해서 사용하면 된다.
앞으로 neural network를 이용해 3d rotation을 regression해야할 경우, neural network이 그냥 6개의 값(a1, a2)을 output으로 출력하게 설계하고 이 6개의 값으로부터 rotation matrix를 복원해낸 뒤, supervision을 걸어주는 식으로 사용하는 방법을 추천한다.
훨씬 성능 좋고, 머리가 덜 아프다. (제일 중요, 안그러면 디버깅이 한 세월)
'Knowledge > Vision' 카테고리의 다른 글
| Camera undistortion visualization(KB model, UCM, DS model) (1) | 2022.12.29 |
|---|---|
| Camera undistortion (UCM, DS model) (0) | 2022.12.29 |
| Camera undistortion (pinhole, KB model) (0) | 2022.12.20 |
| Fisheye camera model(KB, UCM, DS 모델) (0) | 2022.12.07 |
| 3D transformation(R, t) matrix notation (0) | 2022.07.13 |