4Deform: Neural Surface Deformation for Robust Shape Interpolation

내 맘대로 Introduction

 

Implicit Neural Surface Deformation with Explicit Velocity Fields 의 저자랑 동일한 사람이 90% 같은 내용 + 10% 추가 term으로 연달아 CVPR에 낸 논문. 핵심은 modified level set equation으로 형상 간의 interpolation을 질량 보존이 성립하도록 억제하는 것으로 똑같은데, 추가로 surface stretching, shear 같은 표면 형상 변화를 억제하는 loss를 추가한 점이 차이가 있다. 

 

vector field를 요리보고 조리봐서 활용할 수 있는 방법을 계속 캐내는 것이 신기할 뿐이다.

 

메모

내가 볼 땐 전혀 중요한게 아니지만, 저자가 말하길 이전 ICLR 논문에서는 sparse correspondence가 필요한 부분을 수작업으로 했지만, 여기서는 다른 SOTA 알고리즘을 붙였기 때문에 자동이라는 점 sequence에 대해서 적용이 불가능했다는데 여기서는 가능하다는 점인데 <- 이건 사실 좀 의문이다. 그냥 그렇게 안했을 뿐인데.

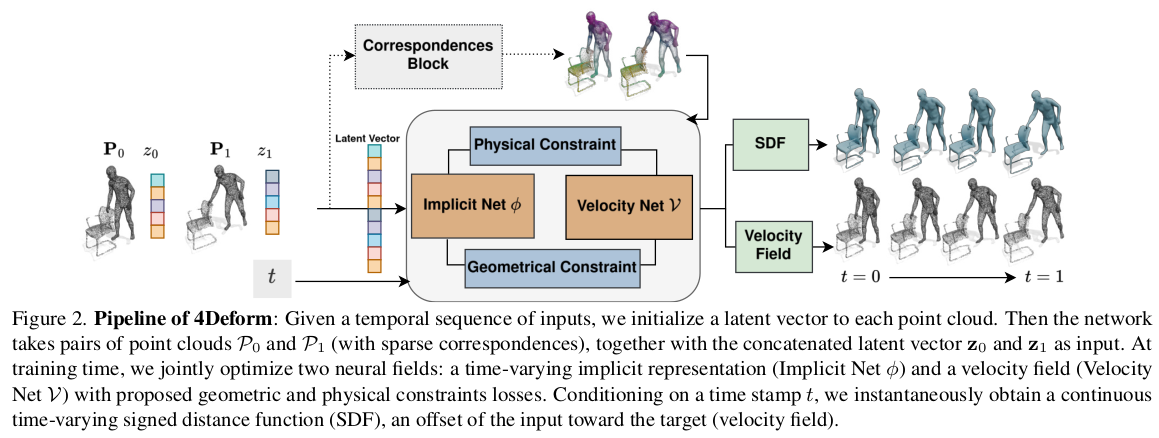
여기까지는 100% ICLR 2025논문과 동일하다. 그냥 LSE (3)에 형상 표면이 찌그러지는 걸 방지하는 (eikonal constraint)를 추가한 modified LSE(4)를 사용하는게 기본이고 vector field가 smooth하고 vector field가 질량을 보존할 수 있도록 하는 (5) regularization을 추가했다.

	사소한 차이는 입력이 point + time + latent z로 변경된 것 point cloud에서 특정 N개를 encoding해서 대표 latent를 하나 만든 뒤 concat한 것이 입력에 추가 된다.  MLP 구조다 보니까 각 point 간의 정보 교류가 제한적인데, global feature를 담고 있는 latent를 추가해줘서 large deform을 커버하는 능력이 조금 더 늘어나길 기대한 것 같다.

학습에 필요한 P0, P1 간의 sparse correspondence가 필요한데, 이건 spectral domain에서 functional map으로 correspondence를 찾는 SOTA 알고리즘을 차용했다.  noisy 데이터셋에 대해서 얼마나 잘 될지는 모르겠으나, 적어도 지금 실험하고 있는 human mesh나 smooth animal에서는 무리 없을 것으로 보임. 이 부분은 핵심이 아니다.

velocity V도 이전 ICLR 2025 논문과 같이 network로 처리한다.  단 여기서 형상마다 vector field가 다를 수 있음을 더 강하게 알려주기 위해서 latent z를 추가했다.  수식(7)은 vector field 자체의 안정성을 수식(8)은 형상 변화에 vector field가 정확하게 기여하길 강제한다. (sparse correspondence를 기반으로)

여기부터가 ICLR2025와 차이가 발생하는 부분이다.  V를 앞에서 질량 보존으로 억제해주긴 했는데 형상의 왜곡 (늘어나고 줄어듬)까지도 더 자연스럽게 만들도록 추가 억제를 하고 싶었다.  그래서 활용한 것이 distortion term 연속체역학에서 stretching, compression, shear 같은 변형을 표현할 때 등장하는 deformation tensor라는게 있는데 이걸 갖고 시작한다. 그냥 단순히 말하면 vector field 곳곳의 크기다.  이게 크면 곳곳의 변형이 큰것이고, 작으면 곳곳의 변형이 작은 것이다. 회전 같은거 빼고 순수 변형만 표현하는 값이 됨.  D = 3X3 이걸 갖고 수식(10)처럼 loss를 구성했다. 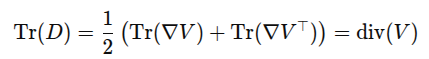 Tr(D)는 div(V)와 같기 때문에 부피의 팽창과 수축을 표현하는 값이고 Tr(D*D)는 전체 그냥 크기기 때문에 부피 팽창 + 왜곡이나 찌그러짐 전부 다를 표현하게 된다.  이 둘의 차이라는 걸 왜곡이나 찌그러짐만을 의미하고 이걸 최소화해서 형상 표면 왜곡을 억제하는 것.

하나 더. 어떤 한 위치 x에서의 변형은 이에 매우 가까운 점 x'에서의 변형과 비슷해야만 한다  어떻게 보면 smoothness와 같음. 따라서 x와 x'가 이동하는 양의 차이가 0 이 되었으면 하는 억제 term이다. ds와 ds'가 x와 x'가 단위시간당 이동하는 양인데 이 둘의 차이가 0이 되도록 한다. 수식(12) 근데 x와 x'는 서로 수식(11)에 의해 서로 엮여있는 점으로 선정했다면 F로 정리가 가능하다. 더 나아가서 어쨌든 표면에서 x를 선정해서 시작할 것이기 때문에 3차원의 모든 방향을 다룰 필요가 없다.  x와 이 위치에서의 sdf를 알고 있으니, normal을 계산할 수 있고 normal을 근거로 tangent plane 상에서 이웃한 두 점의 변형량이 같도록 억제한다.  최종정리하면 수식(14)와 같이 되는 것

당연하게도 latent z는 학습 완료되면 fix되고 계속 inference 때 사용된다.

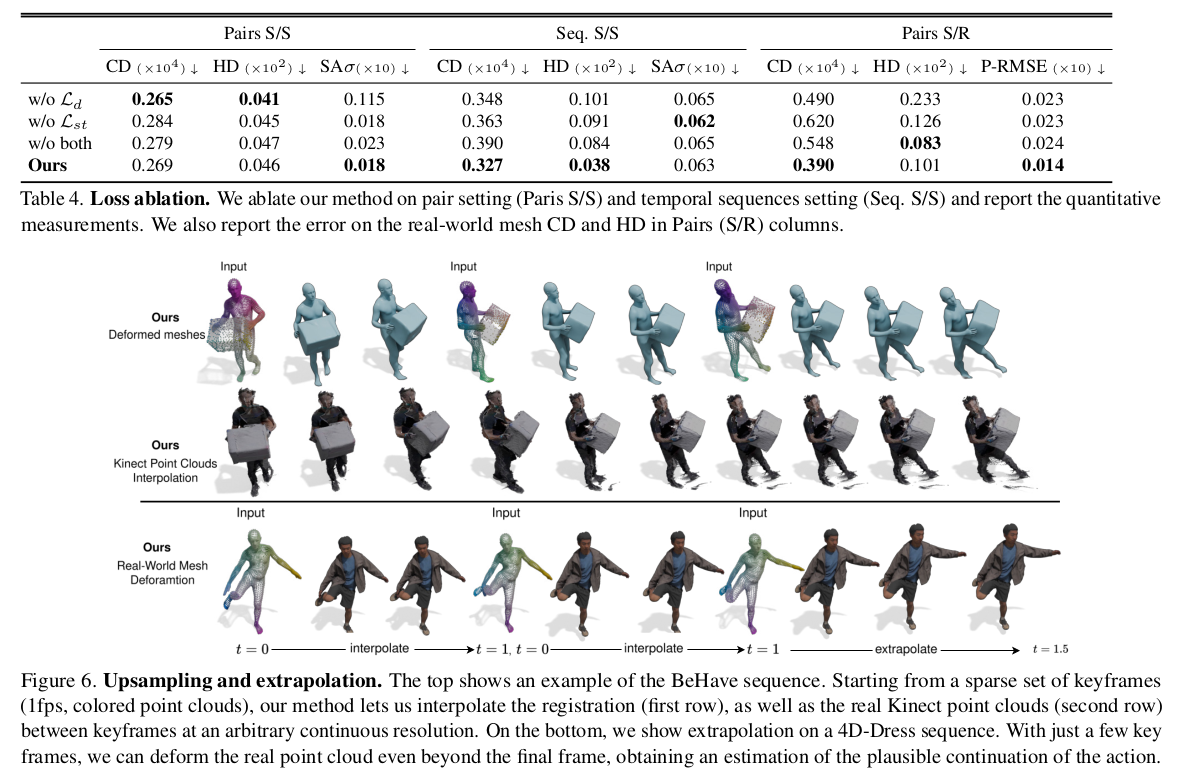
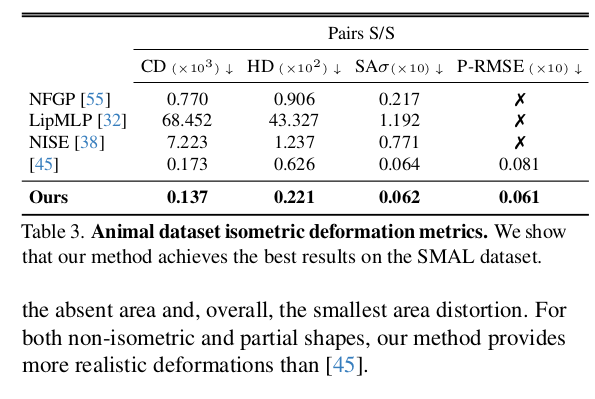	latent z의 힘? 추가 V 억제의 힘 때문에 더 잘된다.

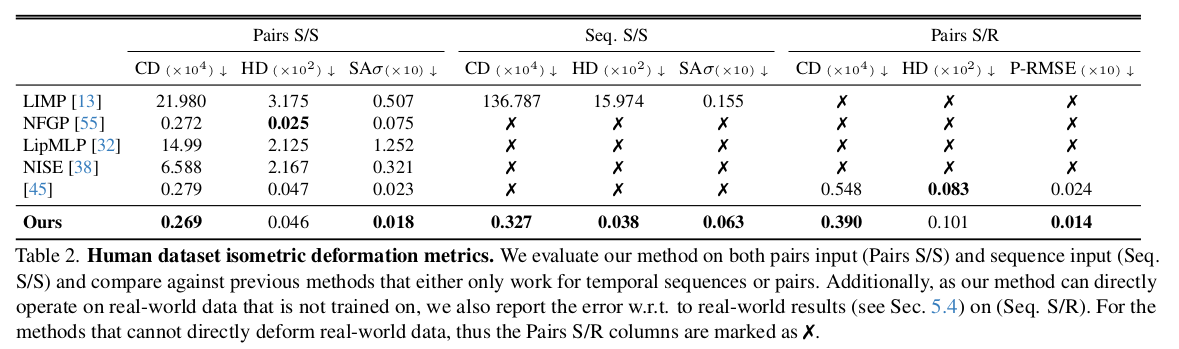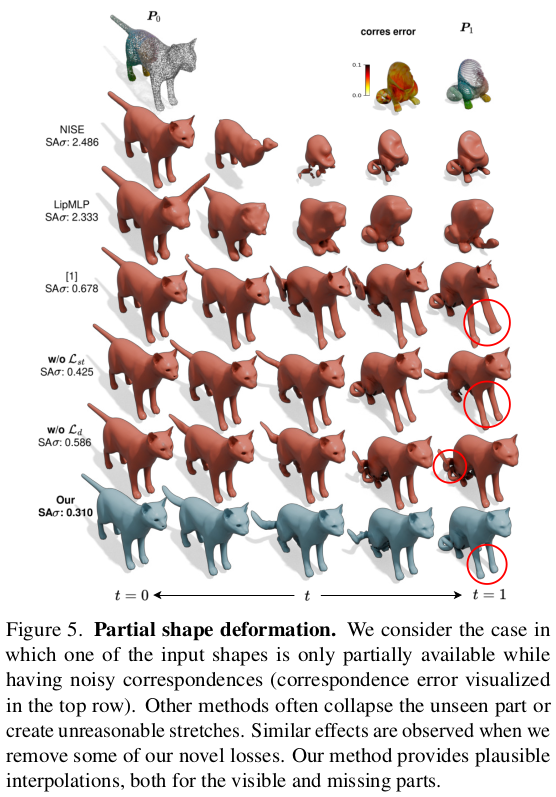
나는 좀 이런 단순 형상에 대한 분석 보다 진짜 실제 쓸 때의 high quality mesh에서의 성능을 보고 싶은데 그게 없는게 아쉽다.