Large Steps in Inverse Rendering of Geometry

내 맘대로 Introduction

 

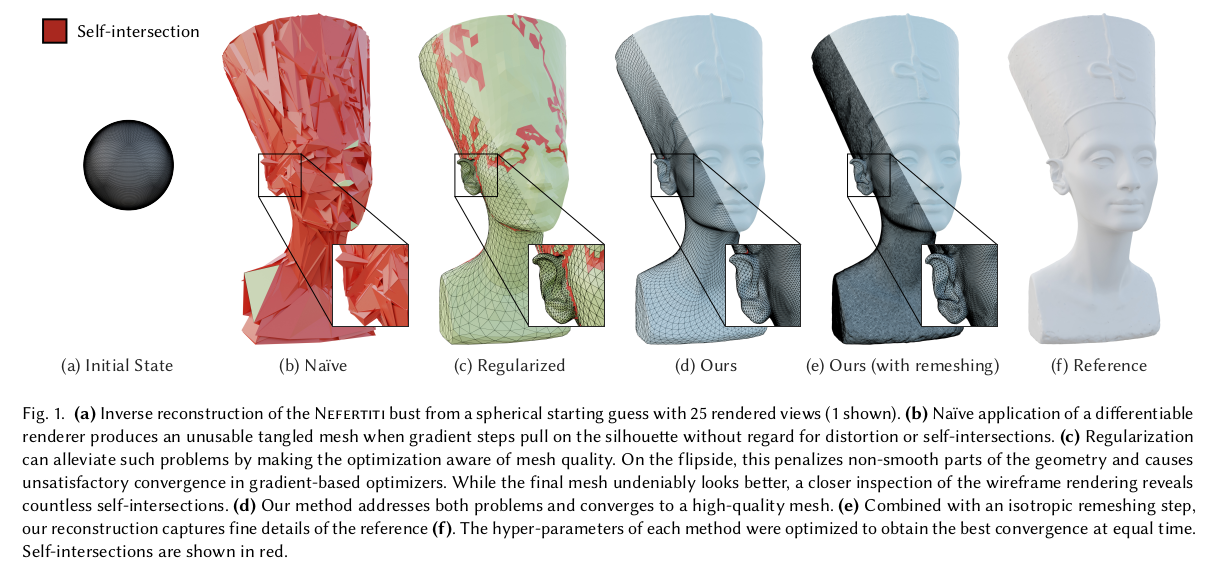
이 논문은 diff.rendering으로 target geometry를 역추정할 때 (DMTet 같은 느낌) 단순히 gradient를 vertex에 흘려보내기만 한다면 위 그림의 (b)처럼 망가지는데, 어떻게 regularization하면 효과적으로 최적화할 수 있을지 방법론을 소개하는 논문이다. 기존 방식은 vertex gradient와 laplacian regularizer 간의 trade-off 지점을 정하는 방식으로 완충했는데, 이 논문은 수학적으로 조금 더 나은 방법을 계산한다. gradient와 regularizer가 싸우도록하는 것이 아니라 gradient 자체를 regularize하는 방식이다. 

 

구체적인 수학은 나도 모름.

 

메모

mesh M이 주어졌을 때 이 mesh에 해당하는 Laplacian operator는 수식(6)과 같이 구한다. mesh의 구조가 변할 때마다 재계산하는 것이 맞다. edge 길이의 변화량으로 가득한 matrix라고 보면 된다.  이 값이 작다는 것은 형상 변화가 작다는 의미이므로 smooth하다고 볼 수 있음.

naive한 방식은 vertex, x를 renderer,R을 이용해 이미지로 내리고 이미지와 비교하는 loss를 통해 dx를 업데이트하는 식이다.  (참고 : 이 논문에서 texture는 직접 풀지 않고 고정된 조명하에 빛 차이로 인한 음영 차이만 다룸) 수식(9)가 그걸 의미하고, 이 수식을 통해 발생하는 gradient는 총 2가지 효과를 만들어낸다. 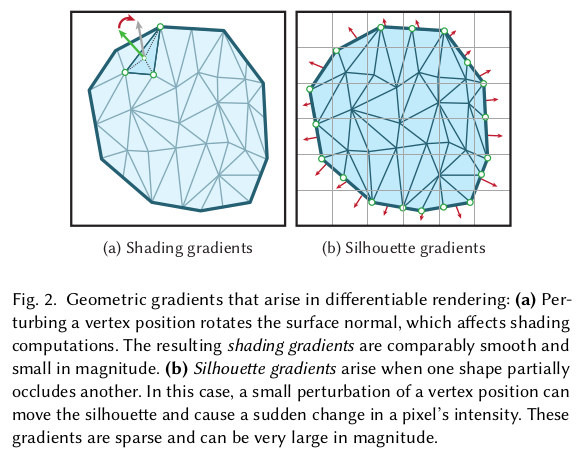 조명 차이에 더 걸맞게 face가 회전하는 힘 (shading gradient) 실루엣이 타겟과 맞도록 확장 이동하는 힘 (silhouette gradient) ----------- 문제는 이 힘이 확실히 의미가 있긴 하지만 모든 face에 제각각 적용돼서 face 간의 연결 관계를 전혀 고려하지 않는다는 것. 따라서 형상이 망가지고 self-penetration같은 문제가 생긴다.

친절하게 그림으로도 설명해주는데 기울어진 직선을 수평선으로 최적화한다고 했을 때 외곽 vertex부터 gradient로 업데이트해보자. 그러면 세번째 그림처럼 끄트머리만 띡하고 업데이트될텐데, graph 구조물인 mesh에서는 그리 바람직한 업데이트는 아니다. 꺾였기 때문이다.  이 상태로 다음 업데이트를 하면 할수록 더 구불구불 업데이트만 될 뿐이다.

그래서 다들했던 것이 뒤에 laplacian regularizer를 "더한 것"이다.  gradient로 변형하는 힘을 그대로 두고, 뒤에다 smooth하게 만드는 힘을 더해서 균형싸움을 하도록 한 것.

확실히 이전 상황보다, 주변 vertex를 고려하긴 해서, smooth해지려고 보상하는 힘이 발생하긴 한다. 하지만 튜닝이 어려워보인다.

이 균형싸움 튜닝 문제를 수학적으로 푸는 방법이 있긴 하다. 2차미분 값을 사용해서 균형을 맞춰주는 것이고 결과도 훌륭하다. 하지만 치명적인 문제로 연산량이 N^3을 웃돈다. 따라서 vertex 개수가 엄청 많은 mesh를 다룰 때는 현실적이지 않다.

그래서! 저자들이 제안한게 연산량이 많이 필요한 Hessian matrix 계산을 identity matrix로 바꿔치기 해버리는 것이다.  mesh가 어떤 대상의 형상을 표현하는 한, smoothness는 어느정도 전제가 되는 상태일테니 1차 미분 laplacian도 그리 크지 않을텐데 2차 미분은 그보다 더 작을 것이다. -> identity로 단순 바꿔치기하는 것이 수학적으로 보지 않고 직관적으로 봐도 그리 이상하지 않음

다른 시각에서 보면 newton method의 2차 파트를 수정한 것이므로 quasi-newton method라고 볼수도 있겠다.

이런 approximated form으로 변형하는 것이 직관을 넘어서 수학적으로도 이점을 제공한다.  어떤 형상 (graph) 위에서 열이 확산되는 수식을 풀어보면 (16)과 같다. 근데 이 때 해는 수식(17)과 같다고 밝혀져 있다. (identity가 들어있는 것이 너무 깔끔하지 않은가) ------------ 이걸 mesh 를 업데이트하는 상황으로 가져와서, mesh가 변형되어가는 것을 마치 열이 퍼져나가는 것과 같은 모양으로 가정하고 수식(16)을 가져와서 사용하겠다고 하면, 앞에서 Hessian을 identity로 변형하면서 저 모양이 같아졌기 때문에 수식(20)과 같이 최종 정리할 수 있다.  수학적인 의미도 있지만, 여기선 그냥 단순히 제곱으로 끝나기 때문에 구현적으로 연산량 관리나 메모리 관리가 쉽다는 장점이 따라온다!

열확산이 퍼져나가는 수식을 차용함으로써 추가로, laplacian 튜닝에서도 조금 더 자유로워진다.  열이라는 것이 퍼져나갈 때 smooth하게 퍼져나가는게 자연의 섭리이기 때문에 저 수식을 가져오는 것 자체가 smoothness를 가져온다는 뜻. 그러니 람다 튜닝에 덜 민감하게 반응하므로 튜닝이 쉬워진다. 1타3피

gradient를 계산하는 것과 더불어 optimizer에 momentum을 같이 써준다면 더 안정적인 업데이트가 가능해진다.

실험적으로 보았을 때 수식(23)같이 쓰는게 제일 좋았다고 한다.

gradient가 아무리 좋다고 참여하는 vertex 개수가 부족하면 태생적 표현력 한계로 복잡한 형상으로는 최적화될 수 없다. 따라서 특정 스텝마다 remeshing을 해서 (edge 길이가 되도록 갖도록 remeshing) vertex를 없애거나 늘려주는 식으로 진행했다.

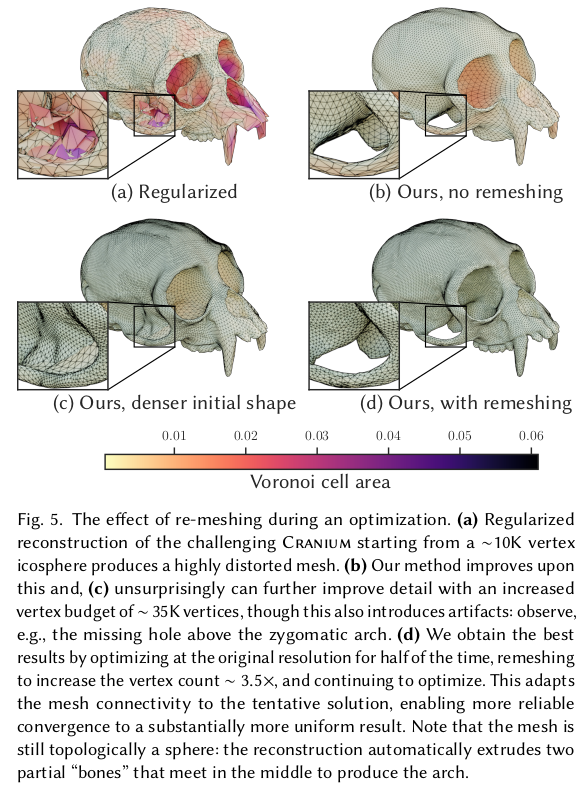람다는 99 정도

view가 많을 수록 잔되는건 당연한 일
	texture는 나중에 후처리로 찾아주는 예제를 보여줌.

속도도 빠르다.  hessian이 없으니 .